LỚP TOÁN THẦY BÌNH
--:--:--

📘 BÀI 2

Môn Toán - Lớp 12

📘 BÀI TẬP TRẮC NGHIỆM ĐÚNG SAI

Question 1. Xét đồ thị của hàm số $y = -x^2 + 5x-4$. Khi đó:

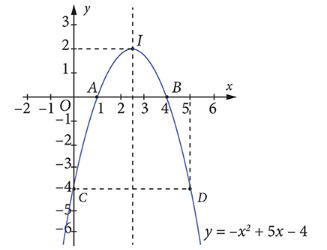
a) có toạ độ đỉnh $I\left(\frac{5}{2}; \frac{9}{4}\right)$
b) trục đối xứng là $x = \frac{5}{2}$
c) giao điểm của đồ thị với trục tung là $C (0;-4)$
d) giao điểm của đồ thị với trục hoành là $A(2;0)$ và $B(3;0)$

Question 2. Cho parabol $(P): y = x^2 - 3x +2$ và đường thẳng $d: y = x−1$.

a) Parabol $(P)$ cắt đường thẳng $d$ hai điểm phân biệt
b) Giao điểm của parabol $(P)$ và đường thẳng $d$ là $(1;0)$
c) Parabol $(P)$ cắt trục hoành tại duy nhất một điểm
d) Parabol $(P)$ cắt trục tung tại điểm có tung độ bằng $-2$

Question 3. Cho hàm số bậc hai $y = ax^2 + bx +c(a \ne 0)$ có đồ thị như hình:

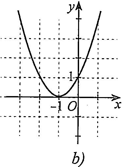
a) $c=1$
b) $a=1$
c) $b = 2$
d) $y = x^2 + 2x$ là hàm số bậc hai có đồ thị như hình vẽ bên trên

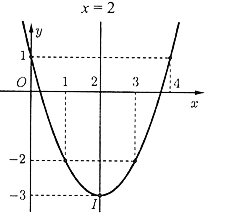
Question 4. Quan sát đồ thị hàm số bậc hai $y = f(x)$ ở hình dưới đây

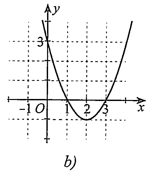
a) $a > 0$;
b) Toạ độ đỉnh $I(2;-1)$, trục đối xứng $x = 2$
c) Đồng biến trên khoảng $(-\infty;2)$; nghịch biến trên khoảng $(2;+\infty)$
d) $x$ thuộc các khoảng $(-\infty;1)$ và $(3;+\infty)$ thì $f(x)>0$

Question 5. Cho hàm số $y = x^2 + 4x -5$. Khi đó:

a) $y \ge0$ khi $x\in [-5;1]$
b) $y \le0$ khi $x\in (-\infty;-5]\cup[1;+\infty)$
c) Giá trị nhỏ nhất của hàm số $y = x^2 +4x-5$ bằng $-9$
d) Với $m = \frac{5}{2}$ thì đường thẳng $d: y = 4x-m$ cắt đồ thị $(P)$ tại $2$ điểm phân biệt có hoành độ $x_1,x_2$ thoả mãn $x_1^2 + x_2^2 = 5$

Question 6. Cho đồ thị hàm số $y = x^2 + 4x + 3$. Khi đó:

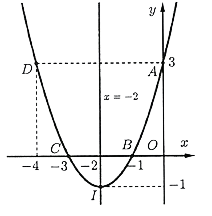
a) Tọa độ đỉnh $I(-2;-1)$
b) Bề lõm parabol hướng xuống
c) Parabol cắt $Ox$ tại các điểm $B(-1;0),C(-3;0)$
d) Đồ thị parabol như hình trên

Question 7. Cho đồ thị hàm số $y = x^2 - 4x +1$. Khi đó:

a) Tọa độ đỉnh $I(2;3)$
b) Phương trình trục đối xứng parabol: $x = 3$
c) Bề lõm parabol hướng lên
d) Đồ thị parabol như hình trên

Question 8. Cho hàm số $y = -x^2 +3$. Khi đó:

a) Tọa độ đỉnh $I(0;3)$
b) Bề lõm parabol hướng lên
c) Hàm số đã cho đồng biến trên khoảng $(0;+\infty)$ và nghịch biến trên khoảng $(-\infty;0)$
d) Giá trị lớn nhất của hàm số là $y_{\max} = 3$, khi $x = 0$

Question 9. Cho hàm số $y = 2x^2 - 2x+1$. Khi đó:

a) Tập xác định: $D = \mathbb{R}$
b) Bề lõm parabol hướng lên
c) Bảng biến thiên:
d) Giá trị lớn nhất của hàm số là $y_{\max} = \frac{3}{2}$, khi đó $x = \frac{1}{2}$

📋 Danh sách slide