Question 1. Hàm số $y = 2x^2 -4x+1$ đồng biến trên khoảng nào?

Question 2. Điểm $I(-2;1)$ là đỉnh của Parabol nào sau đây?

Question 3. Biết hàm số bậc hai $y = ax^2 + bx + c$ có đồ thị là một đường Parabol đi qua điểm $A(-1;0)$ và có đỉnh $I (1;2)$. Tính $a+b+c$.

Question 4. Xác định hàm số $y = ax^2 + bx + c(1)$ biết đồ thị của nó có đỉnh $I\left(\frac{3}{2}; \frac{1}{4}\right)$ và cắt trục hoành tại điểm có hoành độ bằng $2$.

Question 5. Cho parabol $(P)$ có phương trình $y = ax^2 + bx +c$. Tìm $a+b+c$, biết $(P)$ đi qua điểm $A(0;3)$ và có đỉnh $I(-1;2)$.

Question 6. Parabol $y = ax^2 +bx+2$ đi qua hai điểm $M(1;5)$ và $N(-2;8)$ có phương trình là

Question 7. Cho $(P): y = x^2 + bx +1$ đi qua điểm $A(-1;3)$. Khi đó

Question 8. Parabol $y = ax^2 +bx+c$ đi qua $A(8;0)$ và có đỉnh $I(6;-12)$. Khi đó tích $a.b.c$ bằng

Question 9. Cho parabol $y = ax^2 + bx +4$ có trục đối xứng là đường thẳng $x=-\frac{1}{3}$ và đi qua điểm $A(1;3)$. Tổng giá trị $a+2b$ là

Question 10. Cho parabol $y = ax^2 + bx + c$ có đồ thị như hình sau

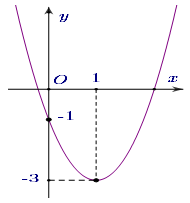
Question 11. Cho parabol $(P): y = ax^2 + bx +c, (a \ne 0)$ có đồ thị như hình bên dưới. Khi đó $2a+b+ 2c$ có giá trị là:

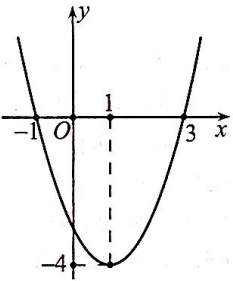
Question 12. Cho hàm số $f(x) = ax^2 + bx + c$ đồ thị như hình. Tính giá trị biểu thức $T = a^2 + b^2 + c^2$.

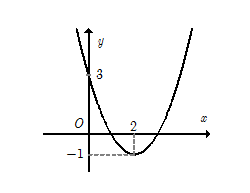
Question 13. Đồ thị hàm số $y = ax^2 + bx+c, (a \ne 0)$ có hệ số $a$ là

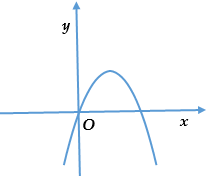
Question 14. Nếu hàm số $y = ax^2 + bx+c$ có $a > 0, b > 0$ và $c<0$ thì đồ thị hàm số của nó có dạng

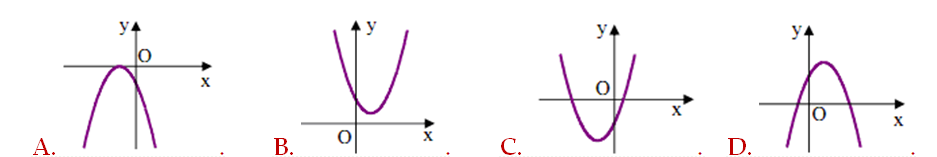
Question 15. Cho hàm số $y = ax^2 + bx + c$ có đồ thị như hình bên dưới. Khẳng định nào sau đây đúng?

Question 16. Cho đồ thị hàm số $y = ax^2 +bx+c$ có đồ thị là parabol trong hình vẽ. Mệnh đề nào sau đây đúng?

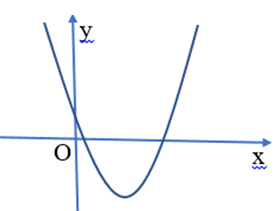
Question 17. Cho hàm số $y = ax^2+bx+c$ có $a<0;b<0;c > 0$ thì đồ thị $(P)$ của hàm số là hình nào trong các hình dưới đây

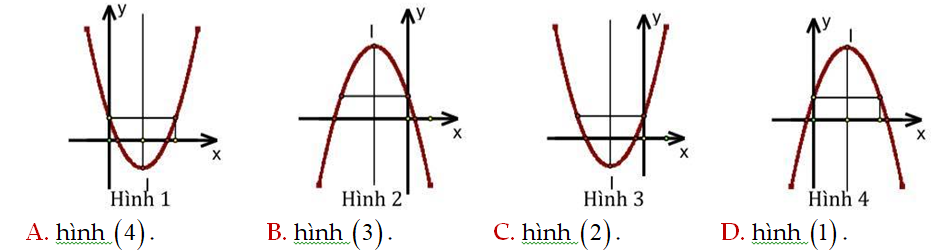
Question 18. Bảng biến thiên sau là của hàm số nào?

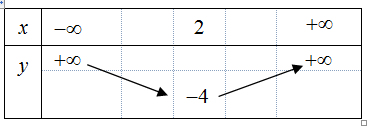
Question 19. Đồ thị trong hình vẽ dưới đây là của hàm số nào trong các phương án A;B;C;D sau đây?

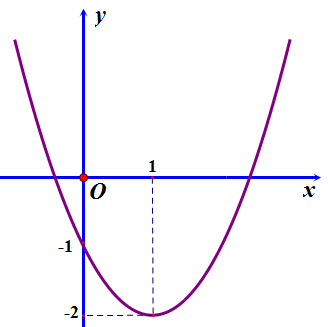
Question 20. Cho parabol $y = ax^2 + bx + c$ có đồ thị như hình sau

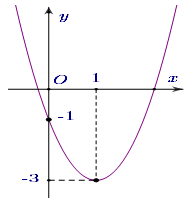
Question 21. Đồ thị hình bên dưới là đồ thị của hàm số bậc hai nào?

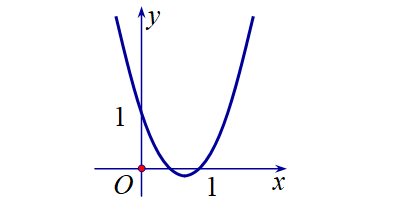
Question 22. Trên mặt phẳng tọa độ $Oxy$ cho Parabol như hình vẽ.

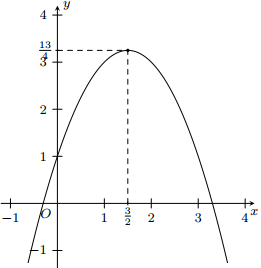
Question 23. Cho parabol $(P): y = ax^2 + bx+c,(a \ne 0)$ có đồ thị như hình bên. Khi đó $2a+b+2c$ có giá trị là

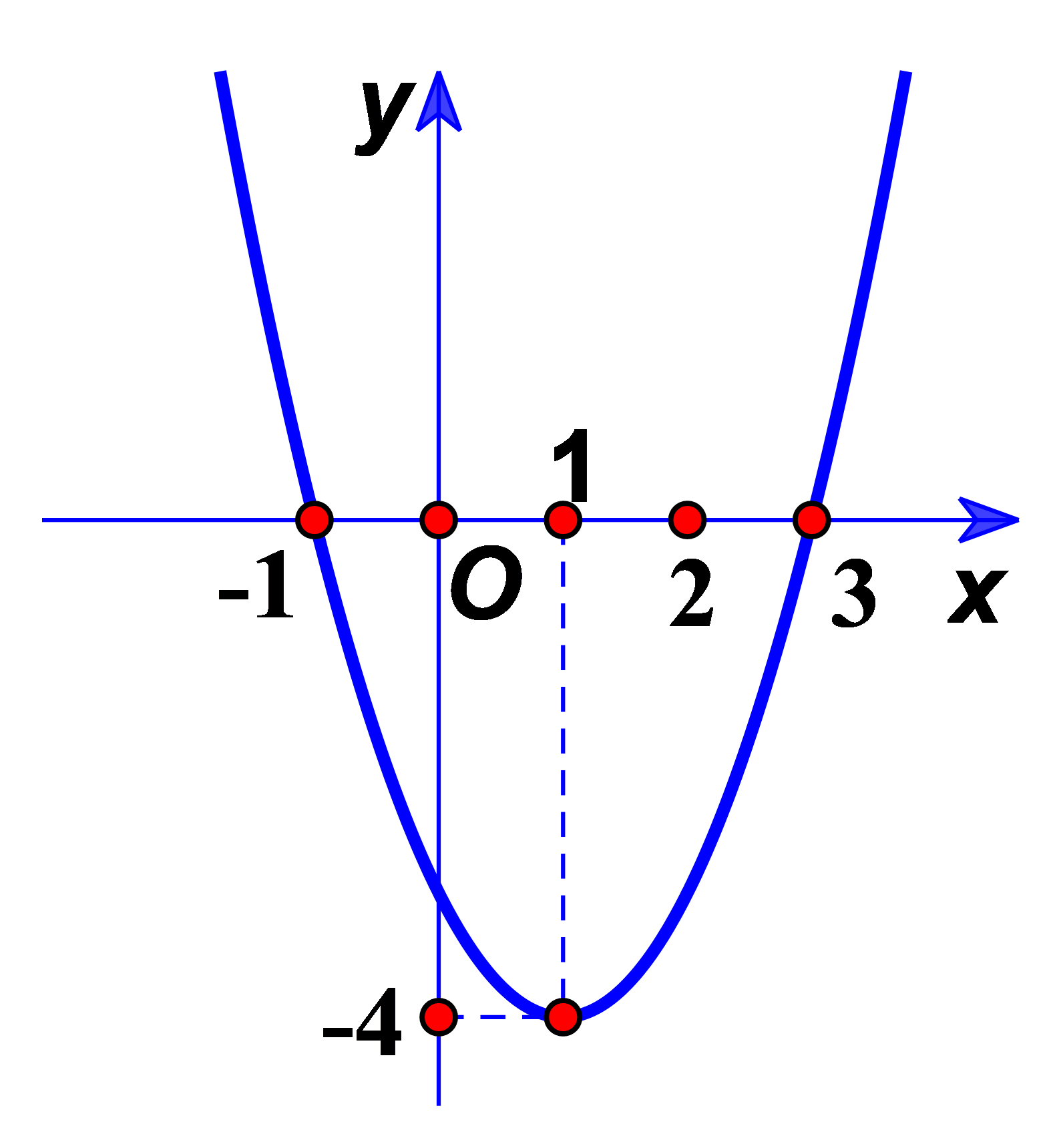
Question 24. Hàm số nào sau đây có đồ thị như hình bên dưới

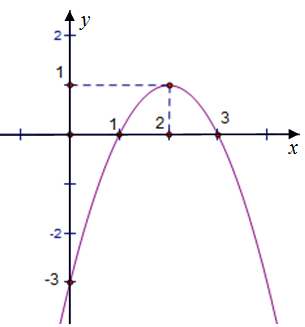
Question 25. Bảng biến thiên ở dưới là bảng biến thiên của hàm số nào trong các hàm số được cho ở bốn phương án A, B, C, D sau đây?

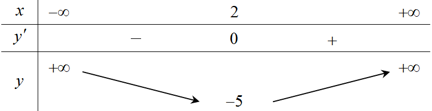
Question 26. Bảng biến thiên sau đây là bảng biến thiên của hàm số nào?

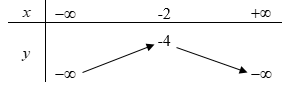
Question 27. Cho hàm số $y = ax^2 + bx + c$ có đồ thị như hình bên dưới. Khẳng định nào sau đây đúng?

Question 28. Cho hàm số $y = ax^2 +bx+c$ có đồ thị là parabol trong hình vẽ. Khẳng định nào sau đây là đúng?

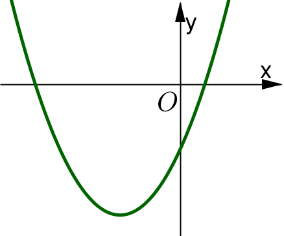
Question 29. Cho hàm số $y = ax^2 +bx+c$ có đồ thị như hình dưới đây. Khẳng định nào sau đây là đúng?

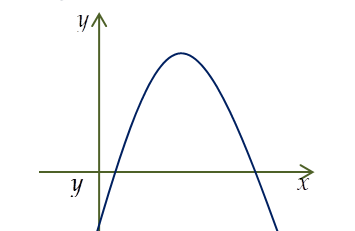
Question 30. Cho parabol $(P): y = ax^2 + bx +c,(a \ne 0)$ có đồ thị như hình bên. Khi đó $2a+b+2c$ có giá trị là

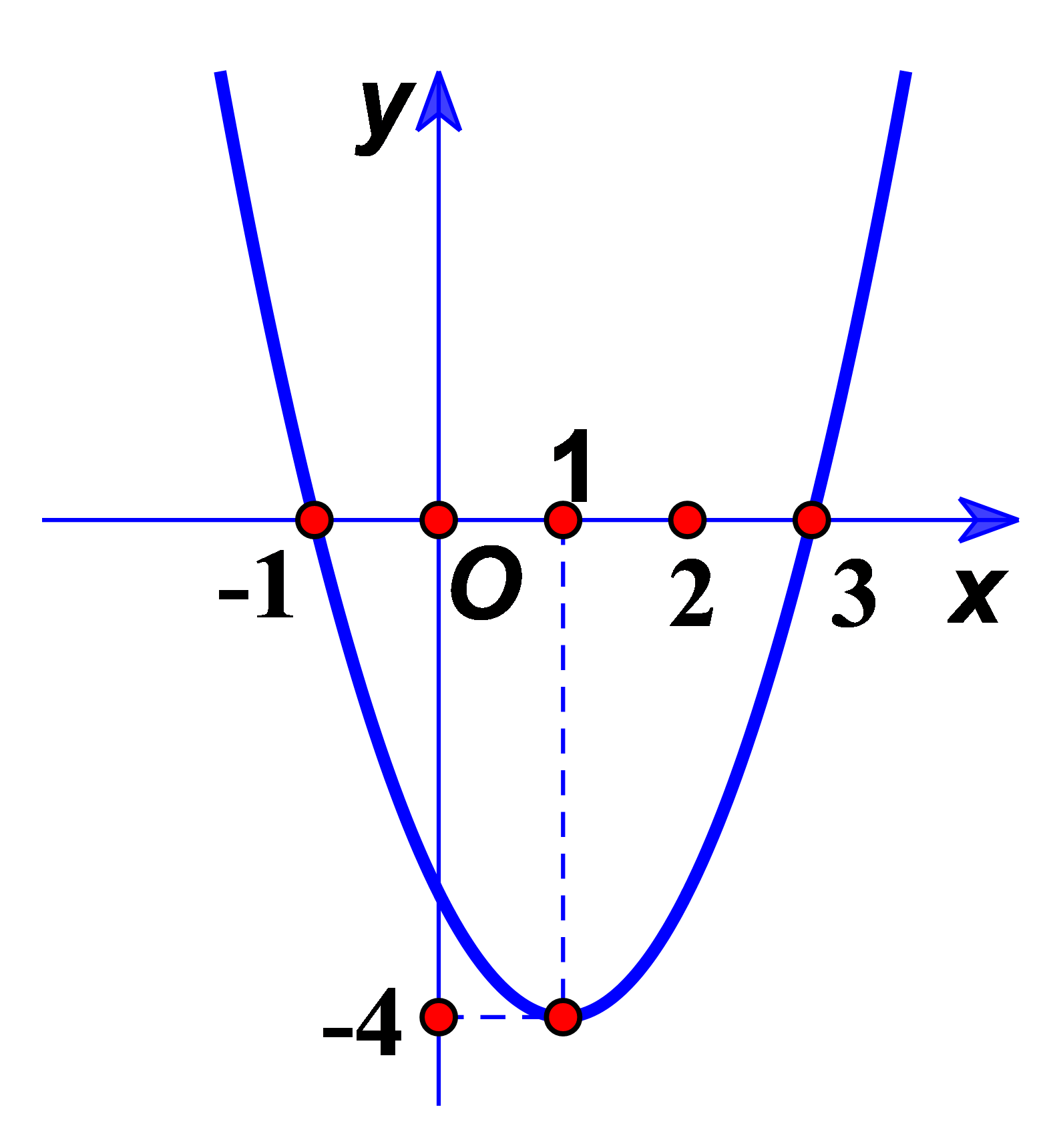
Question 31. Giá trị nhỏ nhất của hàm số $y = x^2 + 2x+3$ đạt được tại

Question 32. Giá trị lớn nhất của hàm số $y = \frac{2}{x^2-5x+9}$ bằng:

Question 33. Tổng giá trị nhỏ nhất và giá trị lớn nhất của hàm số $y = x^2 -4x+3$ trên miền $[-1;4]$ là

Question 34. Giá trị nhỏ nhất của hàm số $y = x^2 + 4|x|+3$ là:

Question 35. Gọi $S$ là tập hợp tất cả các giá trị dương của tham số $m$ để giá trị nhỏ nhất của hàm số $y = f(x) = 4x^2 - 4mx + m^2 – 2m$ trên đoạn $[-2;0]$ bằng $3$. Tính tổng $T$ các phần tử của $S$.

Question 36. Hoành độ giao điểm của đường thẳng $y=1-x$ với $(P): y = x^2 - 2x+1$ là

Question 37. Cho hàm số $y = 2x^2 - 3x-5$. Giá trị của tham số $m$ để đồ thị hàm số $(1)$ cắt đường thẳng $y = 4x + m$ tại hai điểm phân biệt $A(x_1; y_1), B(x_2; x_2)$ thỏa mãn $2x_1^2 + 2x_2^2 = 3x_1x_2 +7$ là

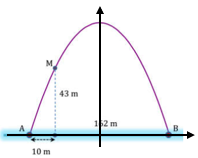
Question 38. Cổng Arch tại thành phố St.Louis của Mỹ có hình dạng là một parabol. Biết khoảng cách giữa hai chân cổng bằng $162$m. Trên thành cổng, tại vị trí có độ cao $43$m so với mặt đất, người ta thả một sợi dây chạm đất. Vị trí chạm đất của đầu sợi dây này cách chân cổng $A$ một đoạn $10$m. Giả sử các số liệu trên là chính xá Hãy tính độ cao của cổng Arch.

Question 39. Cô Tình có $60$m lưới muốn rào một mảng vườn hình chữ nhật để trồng rau, biết rằng một cạnh là tường, cô Tình chỉ cần rào $3$ cạnh còn lại của hình chữ nhật để làm vườn. Em hãy tính hộ diện tích lớn nhất mà cô Tình có thể rào được?

Question 40. Một quả bóng được ném vào không trung có chiều cao tính từ lúc bắt đầu ném ra được cho bởi công thức $h(t) = -t^2 + 2t+3$ (tính bằng mét), $t$ là thời gian tính bằng giây ($t\ge0$). Tính chiều cao lớn nhất quả bóng đạt được?