LỚP TOÁN THẦY BÌNH

📘 BÀI 1

Môn Toán - Lớp 12

📘 BÀI TẬP ĐÚNG SAI

Question 1. Cho hàm số bậc ba $y = f(x)$ có đồ thị là đường cong trong hình dưới đây.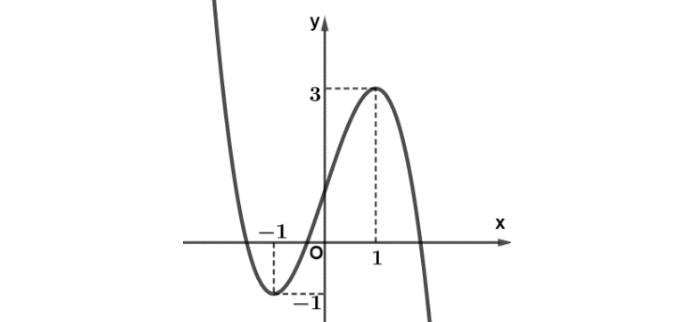

a) Hàm số nghịch biến trên các khoảng $(-\infty;-1)$ và $(1;+\infty)$ True False

b) Đồ thị hàm số có điểm cực tiểu là $(-1;-1)$ True False

c) Gọi a và b lần lượt là tung độ của điểm cực tiểu và điểm cực đại của hàm số ta có $a^2 + b^2 = 10$ True False

d) Phương trình đường thẳng đi qua hai điểm cực trị là $x - y + 2 = 0$ True False

Question 2. Cho hàm số $y=f(x)$ liên tục trên $\mathbb{R}$ và có đạo hàm $f'(x)=(x+1)(x-3)x^2$.

a) Hàm số đạt cực trị tại $x = -1; x=3; x=0$ True False

b) Hàm số $y=f(x)$ nghịch biến trên $(-1;3)$ True False

c) Hàm số $y=f(x)$ đồng biến trên $(-\infty;-1] \cup [3;+\infty)$ True False

d) Hàm số $y=f(3x)$ nghịch biến trên $(-\dfrac{1}{3};1)$ True False

Question 3. Cho hàm số $f(x)$ có bảng biến thiên như sau: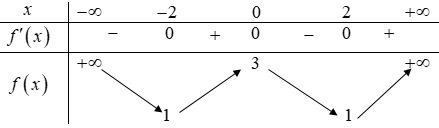

a) Giá trị cực đại của hàm số $f(x)$ bằng 3 True False

b) Hàm số $f(x)$ đồng biến trên khoảng $(1;3)$ True False

c) $f(-10)>f(-3)$ True False

d) Đồ thị hàm số $f(x)$ có ba điểm cực trị là ba đỉnh tam giác có diện tích bằng 4 True False

Question 4. Cho hàm số $y=f(x)$ có bảng biến thiên như sau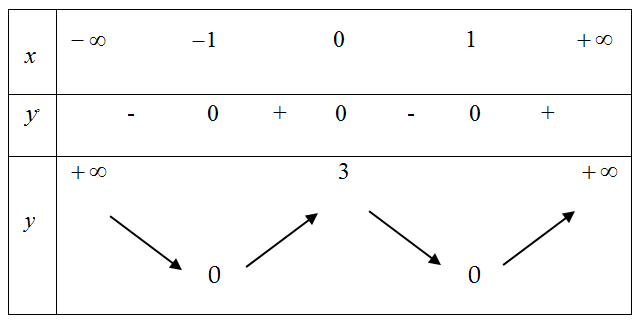

a) Hàm số đồng biến trên các khoảng $(0;3)$ và $(0;+\infty)$ True False

b) Hàm số đồng biến trên khoảng $(2;+\infty)$ True False

c) Đường thẳng đi qua hai điểm cực trị của đồ thị hàm số với hoành độ không âm là $\dfrac{x}{1}+\dfrac{y}{3}=1$ True False

d) Ba điểm cực trị của đồ thị hàm số tạo thành một tam giác có diện tích bằng 3 True False

Question 5. Đồ thị hàm số $y=f(x)=x^3-3x$.

a) Hàm số $f(x)$ luôn đồng biến trên $\mathbb{R}$ True False

b) Hàm số $f(x)$ nghịch biến trên khoảng $(-1;1)$ True False

c) Hàm số $f(x)$ đạt cực tiểu tại điểm $x_0=-1$ True False

d) Đồ thị hàm số $f(x)$ có hai cực trị A và B. Điểm $M(0;-1)$ thuộc đường thẳng AB True False

Question 6. Cho hàm số $y=f(x)$ xác định trên $\mathbb{R}$ và có bảng biến thiên như hình bên dưới. 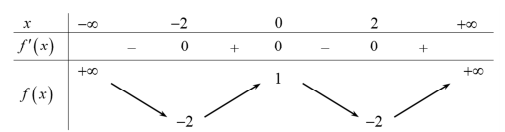Các khẳng định sau đây đúng hay sai?

a) $f(x)$ đồng biến trên khoảng $(-2;0)$ True False

b) $f(x)$ nghịch biến trên khoảng $(0;+\infty)$ True False

c) $\forall x_1,x_2 \in (2;+\infty), x_1 < x_2 \Rightarrow f(x_1) < f(x_2)$ True False

d) $\forall x_1,x_2 \in (-\infty;+\infty), f(x_1) = f(x_2) \Rightarrow x_1 = x_2$ True False

Question 7. Cho hàm số $y=f(x)$ xác định trên $\mathbb{R}$ và có đạo hàm $f'(x)$. Đồ thị của hàm số $f'(x)$ như hình dưới đây. 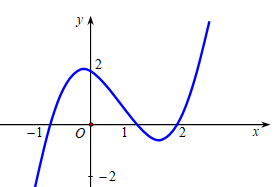Các mệnh đề sau đúng hay sai?

a) Hàm số $y=f(x)$ đồng biến trên khoảng $(-\infty;0)$ True False

b) Hàm số $y=f(x)$ đồng biến trên khoảng $(-1;1)$ True False

c) Hàm số $y=f(x)$ có ba điểm 3 điểm cực trị True False

d) Hàm số $y=f(3-x^2)$ có 6 điểm cực trị True False

Question 8. Cho hàm số $f(x) = \ln x, \forall x \in (0;+\infty)$. Các mệnh đề sau đúng hay sai?

a) Hàm số trên luôn đồng biến trên tập xác định True False

b) Hàm số $y = f(x^2 - 2x)$ có tập xác định là $D=(-\infty;0) \cup (2;+\infty)$ True False

c) Hàm số $y = f(x^2-2x)$ có một điểm cực trị True False

d) Có 6 giá trị nguyên dương của tham số $m$ để hàm số $y=f(x^2-mx)$ luôn đồng biến trên khoảng $(3;+\infty)$ True False

Question 9. Cho hàm số $y=f(x) = \dfrac{-x^2+2x+2}{x+1}$. Các khẳng định sau đây đúng hay sai?

a) Hàm số nghịch biến trên khoảng $(-\infty;-5)$ True False

b) Hàm số đồng biến trên khoảng $(-2;0)$ True False

c) Với mọi $a,b \in (1;+\infty)$ và $a True False

d) Gọi A, B là 2 điểm cực trị của đồ thị hàm số $y=f(x)$. Đường thẳng AB cắt trục hoành tại điểm có hoành độ bằng 1 True False

Question 10. Cho hàm số $y=f(x)$ có bảng biến thiên như hình vẽ. 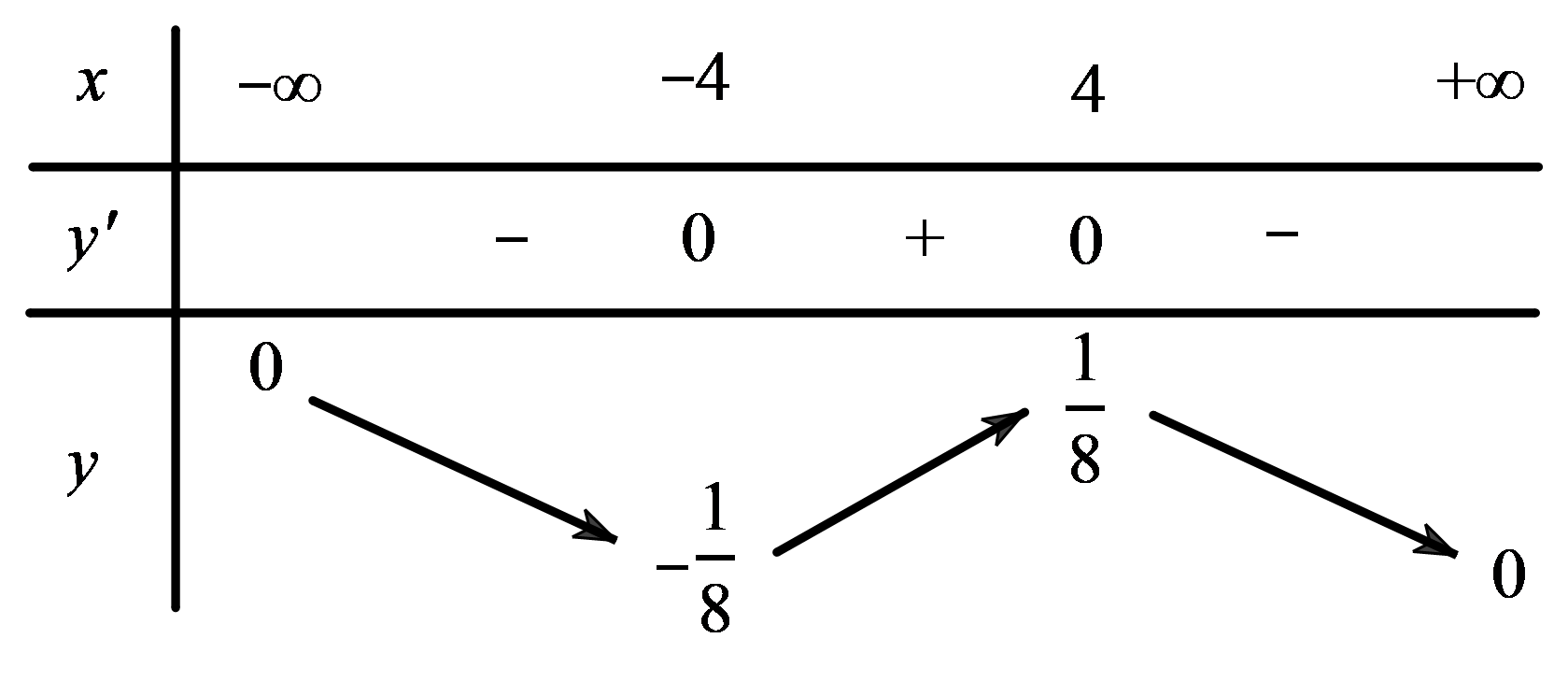Các khẳng định sau đúng hay sai?

a) Trên khoảng $(4;+\infty)$ thì $y'<0$ True False

b) Trên khoảng $(-4;+\infty)$ thì $y'>0$ True False

c) Hàm số đồng biến trên khoảng $(-4;4)$ True False

d) Hàm số nghịch biến trên khoảng $(4;+\infty)$ True False

Question 11. Cho hàm số $y=f(x)$ có đồ thị như hình vẽ 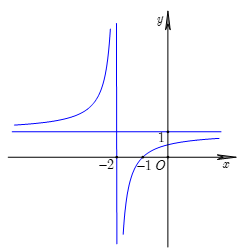Các khẳng định sau đúng hay sai?

a) Hàm số đồng biến trên khoảng $(-\infty;-2)$ True False

b) Hàm số nghịch biến trên khoảng $(-2;+\infty)$ True False

c) Hàm số đồng biến trên khoảng $(-2;+\infty)$ True False

d) Hàm số đồng biến trên khoảng $(0;+\infty)$ True False

Question 12. Đồ thị của đạo hàm bậc nhất $y=f'(x)$ của hàm số $f(x)$ được cho trong hình dưới đây. 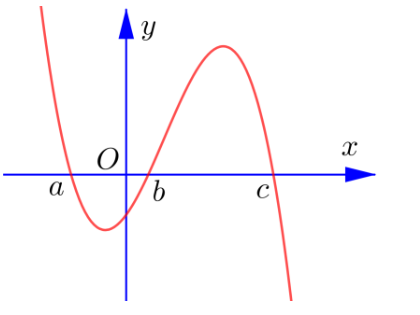Trong mỗi ý ở câu sau, hãy chọn đúng hay sai.

a) Với $\forall x \in (-\infty;a)$ thì $f'(x)>0$ True False

b) Với $\forall x \in (a;c)$ thì $f'(x)<0$ True False

c) Hàm số $y=f(x)$ đồng biến trên khoảng $(b;c)$ True False

d) Hàm số $y=f(x)$ nghịch biến trên khoảng $(c;+\infty)$ True False

Question 13. Cho hàm số bậc bốn $y=f(x)$. Hàm số $y=f'(x)$ có đồ thị như hình dưới đây

a) Hàm số $y=f(x)$ đồng biến trên khoảng $(-\infty;0)$, True False

b) Hàm số $y=f(x)$ đồng biến trên khoảng $(-1;1)$ True False

c) Hàm số $y=f(x)$ nghịch biến trên khoảng $(-\infty;0)$ True False

d) Hàm số $y=f(x)$ nghịch biến trên khoảng $(1;2)$ True False

Question 14. Cho hàm số $y=f(x)=\dfrac{x^2+3x}{x-1}$.

a) Hàm số $f(x)$ đồng biến trên khoảng $(-\infty;1)$ True False

b) Cực đại của hàm số $f(x)$ là 1 True False

c) Hàm số $f(x)$ có ba điểm cực trị True False

d) Hàm số $f(x)$ nghịch biến trên khoảng $(-1;3)$ True False

Question 15. Cho hàm số $y=2^{x^2-3x+\frac{13}{4}}$.

a) Hàm số nghịch biến trên khoảng $(-1;0)$ True False

b) Hàm số đồng biến trên khoảng $(0;1)$ True False

c) Hàm số có giá trị cực tiểu $y_{CT}=2$ True False

d) Hàm số có 2 điểm cực trị True False

Question 16. Cho hàm số $y=\log_2(x^2-4x+5)$ có đồ thị là (C).

a) Hàm số có tập xác định là $D=\mathbb{R}$ True False

b) Hàm số đồng biến trên $\mathbb{R}$ True False

c) Hàm số đạt cực tiểu tại $x=2$ True False

d) Giả sử đồ thị hàm số (C) cắt đường thẳng $(d):y=1$ tại hai điểm A, B và có điểm cực trị là M. Bán kính đường tròn ngoại tiếp tam giác MAB bằng 2 True False

Question 17. Cho hàm số $y = \dfrac{x-1}{x+m}$. Xét tính đúng sai của các mệnh đề sau

a) Hàm số đồng biến trên từng khoảng xác định khi $m \ge -1$ True False

b) Hàm số đồng biến trên khoảng $(-1;+\infty)$ khi $m \ge 1$ True False

c) Hàm số đồng biến trên khoảng $(-\infty;-5)$ khi $m \le 5$ True False

d) Hàm số đồng biến trên khoảng $(-2;7)$ khi $m \ge 2$ True False

Question 18. Cho hàm số $y=f(x)$ có bảng biến thiên như sau:

a) Hàm số $y=f(x)$ đồng biến trên khoảng $(-\infty;2)$ True False

b) Hàm số $y=f(x)$ nghịch biến trên khoảng $(0;3)$ True False

c) Hàm số $y=f(x)$ đạt cực đại tại $x=2$ True False

d) Giá trị cực tiểu của hàm số $y=f(x)$ là $y=-4$ True False

Question 19. Cho hàm số bậc ba $y=f(x)$ có đồ thị là đường cong như hình vẽ sau

a) Hàm số $y=f(x)$ đồng biến trên khoảng $(-\infty;3)$ True False

b) Tổng giá trị cực đại và giá trị cực tiểu của hàm số $y=f(x)$ là 2 True False

c) Hàm số $y=f(x)$ có hai cực trị trái dấu True False

d) Phương trình đường thẳng qua 2 điểm cực trị của đồ thị hàm số $y=f(x)$ là $d:y=-3x$ True False

Question 20. Cho hàm số bậc bốn trùng phương $f(x)$ có bảng biến thiên như sau:

a) Hàm số đồng biến trên $(-1;1)$ True False

b) Độ dài đoạn thẳng nối hai điểm cực tiểu là 2 True False

c) Hàm số $f(2x)$ nghịch biến trên $(0;1)$ True False

d) Số điểm cực trị của hàm số $y=\dfrac{1}{x}[f(x)-1]^4$ là 5 True False

Question 21. Cho hàm số $y=f(x)$ có đạo hàm $f'(x)=(x+1)e^x$.

a) Hàm số nghịch biến trên $(-\infty;-1)$ True False

b) Giá trị cực tiểu của hàm số là 0 True False

c) Hàm số $f(x^2)$ đồng biến trên $(-1;+\infty)$ True False

d) Có 2025 giá trị nguyên của tham số $m$ trong $[-2024;2025]$ để hàm số: $g(x)=f(\ln x)-mx^2+4mx-2$ nghịch biến trên $(e;e^{2024})$ True False

Question 22. Cho hàm số $y=2x^3-3(2m+1)x^2+6m(m+1)x+1$. Xét tính đúng sai của các mệnh đề sau

a) Không tồn tại $m$ để hàm số đã cho nghịch biến trên $\mathbb{R}$ True False

b) Khi $m>1$ thì hàm số đã cho đồng biến trên $\mathbb{R}$ True False

c) Khi $m=\dfrac{5}{6}$ thì hàm số đã cho nghịch biến trên đoạn có độ dài bằng 2 True False

d) Khi $m \le 1$ thì hàm số đã cho đồng biến trên khoảng $(2;+\infty)$ True False

Question 23. Cho một tấm tôn hình chữ nhật có kích thước $80(cm) \times 50(cm)$, người ta cắt đi ở bốn góc của tấm tôn bốn hình vuông bằng nhau để khi gập lại được một chiếc hộp (không nắp). Gọi cạnh hình vuông được cắt đi là $x(cm)$. Xét tính đúng sai của các mệnh đề sau

a) Điều kiện của x là $0 True False

b) Thể tích V của hộp là: $V = x(80-x)(50-x)$ True False

c) Thể tích của hình hộp khi $x=10(cm)$ là $28000(cm^3)$ True False

d) Thể tích của hình hộp lớn nhất là $18000(cm^3)$ True False

Question 24. Cho hàm số $y=x^3-3mx^2+3(2m-1)x+5m-4$. Xét tính đúng sai của các mệnh đề sau

a) Khi $m=1$ thì hàm số đã cho đồng biến trên $\mathbb{R}$ True False

b) Hàm số đã cho nghịch biến trên $\mathbb{R}$ với mọi $m \in \mathbb{R} \setminus \{1\}$ True False

c) Khi $m \le \dfrac{3}{2}$ thì hàm số đã cho đồng biến trên khoảng $(2;3)$ True False

d) Khi $m \le 1$ thì hàm số đã cho đồng biến trên khoảng $(-\infty;5)$ True False

Question 25. Cho hàm số $y=f(x)$ có bảng biến thiên như sau: 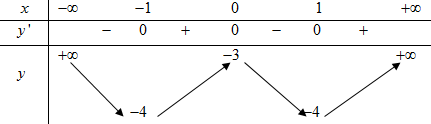Xét tính đúng sai của các mệnh đề sau

a) Điểm cực đại của hàm số là $x=0$ True False

b) Giá trị cực tiểu của hàm số bằng 1 True False

c) Hàm số $y=|f(x)|$ có 3 cực trị True False

d) Hàm số $y=f(|x|)$ có 5 cực trị True False

Question 26. Cho hàm số $f(x)$ liên tục trên $\mathbb{R}$ và có bảng xét dấu của $f'(x)$ như sau: 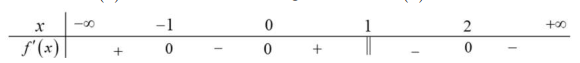Xét tính đúng sai của các mệnh đề sau

a) Hàm số đạt cực tiểu tại $x=-1$ True False

b) Hàm số đã cho có 3 cực trị True False

c) Hàm số $y=f(|x|)$ có 3 cực trị True False

d) Hàm số $y=f(-2x+1)$ có 5 cực trị True False

Question 27. Cho hàm số bậc ba $y=f(x)$ có đồ thị như hình vẽ. 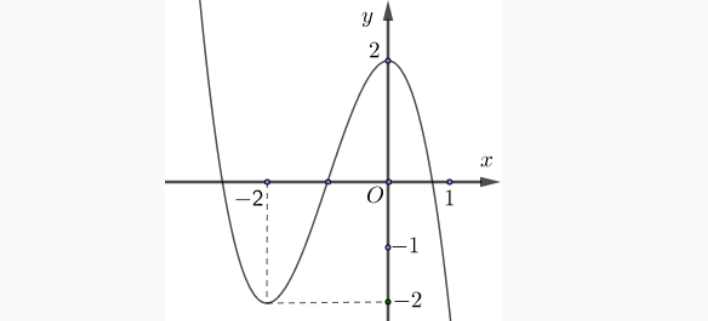Xét tính đúng sai của các mệnh đề sau

a) Hàm số đạt cực đại tại $x=2$ True False

b) Hàm số đã cho có 2 cực trị True False

c) Hàm số $y=|f(x)|$ có 5 cực trị True False

d) Hàm số $y=f(-x^2+x)$ có 3 cực tiểu True False

Question 28. Cho hàm đa thức bậc năm $y=f(x)$ và đồ thị hàm số $y=f'(x)$ trên $\mathbb{R}$ như hình vẽ. 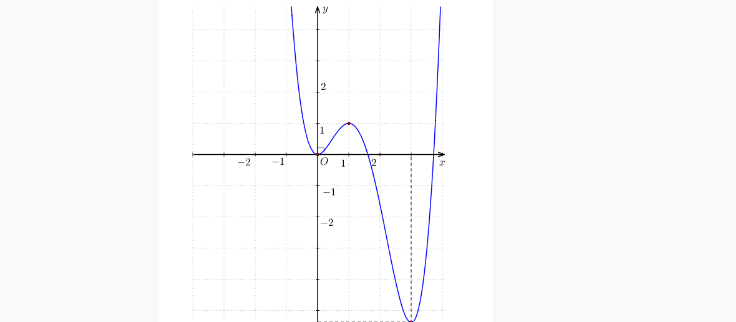Xét tính đúng sai của các mệnh đề sau

a) Hàm số đạt cực đại tại $x=3$ True False

b) Hàm số đã cho có 3 cực trị True False

c) Hàm số $y=f(3x-2024)$ có 2 cực trị True False

d) Hàm số $g(x)=f(x)+2x$ có 3 cực trị True False

Question 29. Cho hàm số $y=f(x)$ có bảng biến thiên như sau 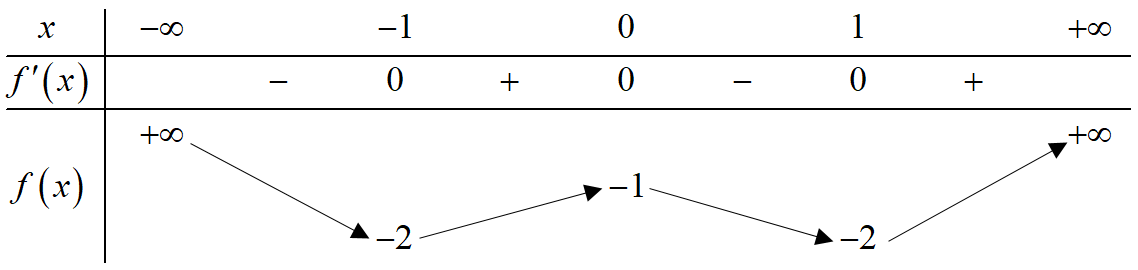Xét tính đúng sai của các mệnh đề sau:

a) Hàm số $y=f(x)$ có 3 điểm cực trị True False

b) Giá trị cực đại của hàm số $y=f(x)$ là 0 True False

c) Hàm số $y=|f(x)|$ có 3 điểm cực tiểu True False

d) Hàm số $g(x)=f^3(x)+3f^2(x)+2020$ có 7 điểm cực trị True False

Question 30. Cho hàm số $f(x) = ax^3 + bx^2 + cx + d$ $(a,b,c,d \in \mathbb{R})$ có bảng biến thiên như sau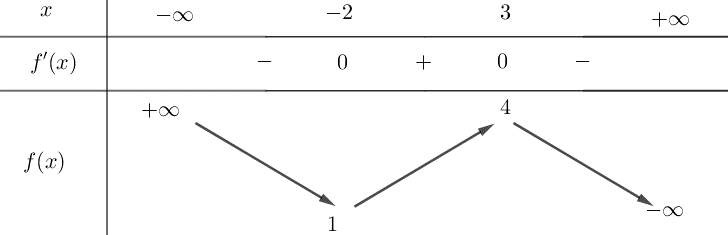

a) Hàm số đạt cực đại tại điểm $x=4$ True False

b) Giá trị cực tiểu của hàm số là $y=1$ True False

c) Hàm số $y = f(x)$ đồng biến trên khoảng $(-1;1)$ True False

d) Hàm số $y=f(x)$ có 3 số dương trong các hệ số $a,b,c,d$ True False

Question 31. Cho hàm số $y=f(x)=x^3-3mx^2+3(2m-1)x+1$, $m$ là tham số.

a) Với $m=0$, hàm số có dạng $y=x^3-3x+1$ True False

b) Với $m=0$, điểm cực đại của đồ thị hàm số là $(-1;2)$ True False

c) Hàm số $y=f(x)=x^3-3mx^2+3(2m-1)x+1$, đạt cực đại tại $x=0$, khi $m=\dfrac{1}{2}$ True False

d) Hàm số đồng biến trên $(-\infty;+\infty)$ khi và chỉ khi $m=1$ True False

Question 32. Cho hàm số $y=f(x)=-\dfrac{1}{3}x^3+(m-1)x^2+(m-3)x+2$, trong đó $m$ là tham số. Xét tính đúng sai của các mệnh đề sau?

a) $y'=-x^2+2(m-1)x+m-3$ True False

b) Khi $m=0$, hàm số nghịch biến trên $\mathbb{R}$ True False

c) Có ít nhất một giá trị của tham số $m$ để hàm số đồng biến trên $\mathbb{R}$ True False

d) Có tất cả 3 giá trị nguyên của tham số $m$ để hàm số nghịch biến trên $\mathbb{R}$ True False

Question 33. Cho hàm số $y=\dfrac{1}{3}mx^3-(m-1)x^2+3(m-2)x+\dfrac{1}{3}$. Xét tính đúng sai của các mệnh đề sau?

a) Tập xác định của hàm số là $D=\mathbb{R} \setminus \{3\}$ True False

b) Hàm số có đạo hàm là $y'=mx^2-2(m-1)x+3(m-2)$ True False

c) Đồ thị hàm số đi qua điểm $M(1;1)$ khi $m=\dfrac{17}{7}$ True False

d) Với $m \ge \dfrac{2}{3}$ thì hàm số đã cho đồng biến trên khoảng $[2;+\infty)$ True False

Question 34. Cho hàm số $y=\dfrac{x+4}{x+m}$ với $m$ là tham số. Xét tính đúng, sai của các khẳng định sau:

a) Tập xác định của hàm số là $\mathbb{R} \setminus \{-m\}$ True False

b) Khi $m=1$, hàm số nghịch biến trên các khoảng $(-\infty;-1)$ và $(-1;+\infty)$ True False

c) Hàm số nghịch biến trên từng khoảng xác định $\Leftrightarrow m < 4$ True False

d) Hàm số nghịch biến trên khoảng $(6;+\infty) \Leftrightarrow -6 True False

Question 35. Cho hàm số $y=\dfrac{mx+3m-4}{x-m}$ với $m$ là tham số. Xét tính đúng, sai của các khẳng định sau:

a) Hàm số có hai điểm cực trị True False

b) Khi $m=-1$, hàm số đồng biến trên $\mathbb{R} \setminus \{-1\}$ True False

c) Hàm số đồng biến trên từng khoảng xác định $\Leftrightarrow -4 True False

d) Gọi S là tập hợp tất cả các giá trị nguyên của $m$ để hàm số đồng biến trên khoảng $(-\infty;-2)$. Số phần tử của S là 3 True False

Question 36. Cho hàm số $y=\dfrac{-x+1}{x+m}$ với $m$ là tham số, $x \ne -m$. Xét tính đúng, sai của các khẳng định sau:

a) $y' = \dfrac{-m-1}{(x+m)^2}, \forall x \ne -m$ True False

b) Khi $m=-2$, hàm số đồng biến trên các khoảng $(-\infty;2)$ và $(2;+\infty)$ True False

c) Hàm số đồng biến trên từng khoảng xác định khi $m<-1$ True False

d) Gọi S là tổng các giá trị nguyên của tham số $m$ để hàm số nghịch biến trên $(-\infty;-3)$. Khi đó $S=9$ True False

Question 37. Cho hàm số $y=\dfrac{mx+4m}{x+m}$ với $m$ là tham số, $x \ne -m$. Xét tính đúng, sai của các khẳng định sau:

a) Khi $m=-1$, hàm số đồng biến trên các khoảng $(-\infty;1)$ và $(1;+\infty)$ True False

b) Hàm số luôn có hai đường tiệm cận True False

c) Gọi S là tập hợp tất cả các giá trị nguyên của $m$ để hàm số nghịch biến trên các khoảng xác định. Số phần tử của S là 3 True False

d) Gọi T là tập hợp tất cả các giá trị nguyên của $m$ để hàm số nghịch biến trên $(5;+\infty)$. Khi đó $T=32$ True False

Question 38. Cho hàm số $y=\dfrac{(m+1)x^2-2mx+6m}{x-1}$, ($m$ là tham số). Các mệnh đề sau đúng hay sai?

a) Tập xác định của hàm số đã cho là $D=\mathbb{R} \setminus \{1\}$ True False

b) Với $m=0$ thì hàm số có dạng $y=\dfrac{x^2}{x-1}$ True False

c) Hàm số $y=\dfrac{x^2}{x-1}$ nghịch biến trên $(1;+\infty)$ True False

d) Hàm số đồng biến trên mỗi khoảng xác định khi và chỉ khi $m$ thuộc $[a;b]$. Khi đó $a+5b=0$ True False

Question 39. Cho hàm số $y=\dfrac{x^2-3x+2}{x+2}$ (C). Các mệnh đề sau đúng hay sai?

a) Ta luôn có $y=\dfrac{x^2-3x+2}{x+2}=x-5+\dfrac{12}{x+2}$ True False

b) Đồ thị hàm số (C) có 2 điểm cực trị True False

c) Điểm $M(0;-1)$ là giao điểm của trục tung với tiệm cận xiên của (C) True False

d) Đồ thị hàm số (C) có 2 cực trị và đường thẳng đi qua 2 điểm cực trị có phương trình $y=2x-3$ True False

Question 40. Cho hàm số $y=\dfrac{x^2-x+1}{x}$ có đồ thị là (C).

a) Đạo hàm $y'$ của hàm số là $y'=1-\dfrac{1}{x^2}, \forall x \ne 0$ True False

b) Hàm số đã cho đồng biến trên khoảng $(-\infty;-1)$ True False

c) Giá trị cực đại của hàm số đã cho lớn hơn giá trị cực tiểu của hàm số True False

d) Gọi A, B là hai điểm cực trị của đồ thị (C), diện tích tam giác OAB bằng 2 True False

Question 41. Cho hàm số $y=f(x)=\dfrac{x^2+x+2}{x-1}$ có đồ thị là (C).

a) Tập xác định của hàm số là $D=\mathbb{R} \setminus \{1\}$ True False

b) Hàm số đã cho nghịch biến trên khoảng $(1;4)$ True False

c) Hai điểm cực trị của đồ thị (C) đối xứng nhau qua điểm $I(1;3)$ True False

d) Hàm số $g(x)=f(f'(x))$ có 2 điểm cực đại và 1 điểm cực tiểu True False

Question 42. Cho hàm số $y=\dfrac{x^2+mx+m}{x+m}$. Xét tính đúng, sai của các khẳng định sau:

a) Với $m=1$ đồ thị hàm số cắt trục tung tại điểm $A(0;1)$ True False

b) Với $m=1$ hàm số nghịch biến trên khoảng $(-2;0)$ True False

c) Với $m=1$ đồ thị hàm số nhận $x=-2; x=0$ làm hai điểm cực trị True False

d) Có hai giá trị nguyên của tham số $m$ để hàm số đạt cực đại tại $x=2$ True False

Question 43. Cho hàm số $y=\dfrac{x^2+mx-1}{x-1}$ xét tính đúng sai của các mệnh đề sau

a) Với $m=1$ đồ thị hàm số nhận đường thẳng $x=1$ làm tiệm cận đứng True False

b) Với $m=1$ hàm số đồng biến trên khoảng $(-\infty,1)$ True False

c) Với $m=1$ hàm số nhận $x=0;x=2$ làm hai điểm cực trị True False

d) Có 2024 giá trị nguyên dương của tham số $m \in (-2024;2024)$ để hàm số có cực đại và cực tiểu True False

Question 44. Cho hàm số $y=x^4-2mx^2+m$, với $m$ là tham số. Xét tính đúng, sai của các khẳng định sau:

a) Khi $m=1$ thì hàm số là $y=x^4-2x^2+1$ True False

b) Khi $m=1$ thì hàm số có $y'=4x^3-4$ True False

c) Khi $m=1$ thì hàm số có 3 cực trị True False

d) Đồ thị của hàm số cắt trục hoành tại bốn điểm phân biệt khi $m>1$ True False

Question 45. Cho hàm số $y=x^4-(m-1)x^2+m-2$, với $m$ là tham số. Xét tính đúng, sai của các khẳng định sau:

a) Hàm số $y=f(x)$ có tập xác định là $\mathbb{R}$ True False

b) Khi $m=0$ hàm số $y=f(x)$ có ba cực trị True False

c) Khi $m=0$ hàm số $y=f(x)$ đồng biến trên $(-\infty;0)$ True False

d) Để đồ thị hàm số cắt trục hoành tại 4 điểm phân biệt thì $m \in (2;+\infty) \setminus \{3\}$ True False

Question 46. Cho hàm số $y=f(x)$ có đạo hàm $f'(x)=(x^2-1)(x-4)$ với mọi $x \in \mathbb{R}$?

a) Hàm số có 3 điểm cực trị True False

b) Hàm số đồng biến trong khoảng $(-1;1)$ True False

c) Tiếp tuyến của đồ thị hàm số luôn có hệ số góc dương khi hoành độ tiếp điểm lớn hơn 1 True False

d) Hàm số $g(x)=f(3-x)$ đạt cực đại tại $x=1$ True False

Question 47. Cho hàm số $y=f(x)$ có đạo hàm $f'(x)$ trên khoảng $(-\infty;+\infty)$. Biết đồ thị (C) của hàm số $y=f(x)$ như hình vẽ dưới đây.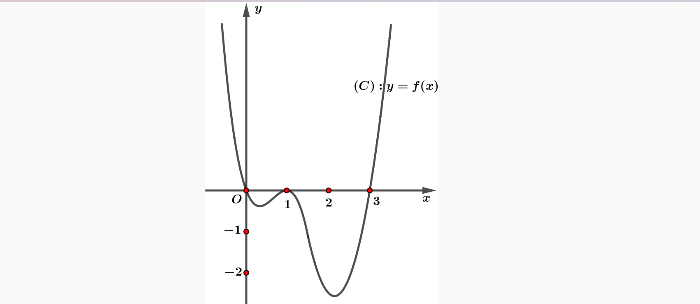

a) Điểm cực đại của đồ thị (C) là $x=1$ True False

b) Hàm số $y=f(x)$ đồng biến trong khoảng $(2;+\infty)$ True False

c) Đồ thị (C'): $y=f'(x)$ luôn cắt trục hoành tại 3 điểm phân biệt True False

d) Đồ thị của hàm số $y=[f(x)]^2$ có bao ba điểm cực tiểu? True False

Question 48. Cho hàm số $y=f(x)$ có bảng biến thiên như hình vẽ bên. Xét tính đúng, sai của các khẳng định sau: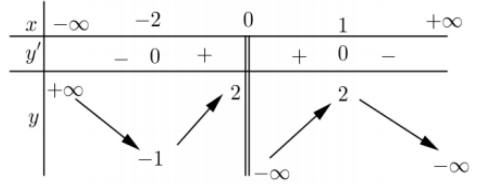

a) Hàm số $f(x)$ đạt cực tiểu tại $x=-2$ True False

b) Điểm cực tiểu của đồ thị hàm số $y=f(x)$ là $(-2;-1)$ True False

c) Đường thẳng $y=x+1$ đi qua hai điểm cực trị của đồ thị hàm số đã cho True False

d) Hàm số $y=g(x)=f(2x-3)$ đạt cực tiểu tại điểm $x=\dfrac{5}{2}$ True False

Question 49. Cho hàm số $y=f(x)$ có bảng biến thiên như sau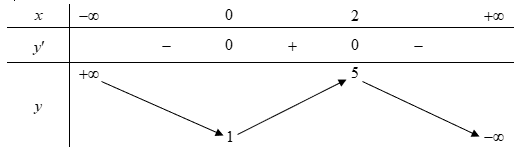

a) Hàm số $f(x)$ đạt cực tiểu tại $x=0$ True False

b) Hàm số có hai cực trị True False

c) Khoảng cách giữa hai điểm cực trị là 3 True False

d) Đường thẳng $y=2x+1$ đi qua hai điểm cực trị True False

Question 50. Cho hàm số $y=|x+1|(x-2)$. Khi đó:

a) Hàm số có 2 điểm cực trị True False

b) Hàm số nghịch biến trên khoảng $(-\infty;-1)$ True False

c) Hàm số đồng biến trên các khoảng $(-\infty;-1)$ và $(\dfrac{1}{2};+\infty)$ True False

d) Hàm số nghịch biến trên khoảng $(-1;\dfrac{1}{2})$ và $(\dfrac{1}{2};+\infty)$ True False

Question 51. Cho hàm số $y=f(x)$. Đồ thị hàm số $y=f'(x)$ như hình bên 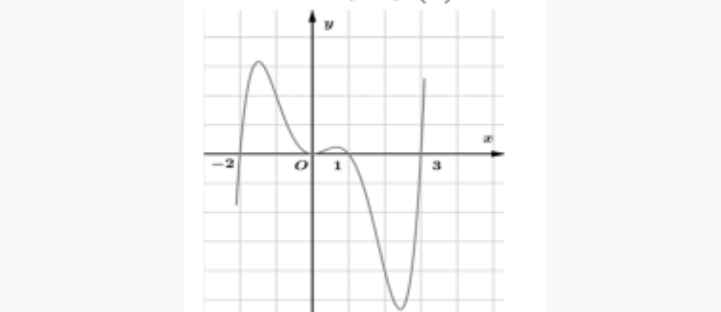Khi đó:

a) Hàm số $y=f(x)$ có 4 điểm cực trị True False

b) Hàm số $y=f(x)$ đồng biến trên khoảng $(-\infty;-2)$ True False

c) Hàm số $y=f(x^2)$ đồng biến trên khoảng $(\sqrt{3};+\infty)$ True False

d) Hàm số $y=f(x^2)$ có 5 điểm cực trị True False

Question 52. Cho hàm số bậc bốn $y=f(x)$ có đồ thị hàm số $y=f'(x)$ như hình vẽ bên. 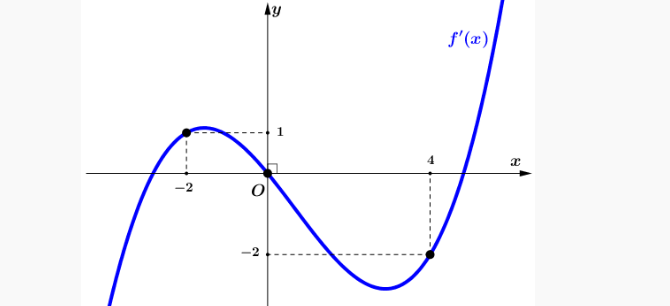Xét tính đúng sai của các mệnh đề sau:

a) Hàm số $y=f(x)$ có hai điểm cực trị True False

b) Hàm số $y=f(x)$ đạt cực đại tại $x=0$ True False

c) Hàm số $h(x)=5f(|2-x|)+2024$ có 5 điểm cực trị True False

d) Hàm số $g(x)=4f(x^2-4)+x^4-8x^2$ có 4 điểm cực tiểu True False

Question 53. Cho hàm số bậc ba $y=f(x)$ có đồ thị như hình vẽ. 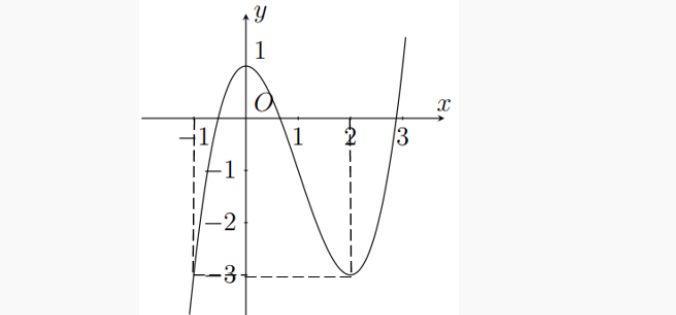Xét tính đúng sai của các mệnh đề sau:

a) Hàm số $y=f(x)$ có hai điểm cực trị True False

b) Điểm cực tiểu của đồ thị hàm số là $x=2$ True False

c) Hàm số $y=f(f(x))$ có tất cả 5 điểm cực trị True False

d) Cho hàm số $h(x)$ có đạo hàm $h'(x)=f(x^3-3x^2+m)+3$. Khi đó có tất cả 10 giá trị nguyên của tham số $m$ để hàm số $h(x)$ có hoành độ cực trị thuộc đoạn $[-1;2]$ True False

Question 54. Cho hàm số đa thức bậc bốn $y=f(x)$ thỏa mãn $f(0)=\dfrac{1}{2}$, hàm số $f'(x)$ có đồ thị như hình vẽ. 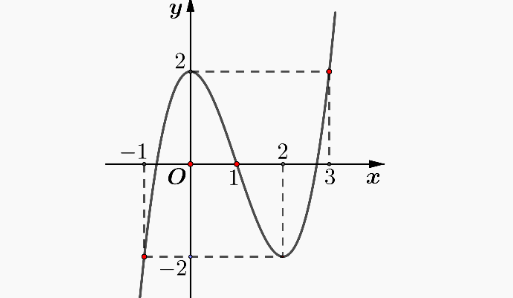Xét tính đúng sai của các mệnh đề sau:

a) Hàm số $y=f'(x)$ đạt cực đại tiểu tại $x=2$ True False

b) Hàm số $y=f(x)$ đạt cực đại tại $x=2$ True False

c) Hàm số $y=f(x^2)$ có 4 điểm cực trị True False

d) Hàm số $g(x)=|18f(1-\dfrac{x}{3})-x^2|$ có 7 điểm cực trị True False

📘 BÀI 1

📘 BÀI TẬP ĐÚNG SAI

📋 Danh sách slide