CHUYÊN ĐỀ: ỨNG DỤNG ĐẠO HÀM
Môn Toán - Lớp 12
TÓM TẮT KIẾN THỨC
Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
Định Nghĩa
Cho hàm số \( y = f(x) \) xác định trên tập hợp \( D \).
- Số \( M \) được gọi là giá trị lớn nhất của hàm số \( y = f(x) \) trên \( D \) nếu \( f(x) \le M, \forall x \in D \) và \( \exists x_0 \in D, f(x_0) = M \).
Ký hiệu: \( M = \max_{D} f(x) \). - Số \( m \) được gọi là giá trị nhỏ nhất của hàm số \( y = f(x) \) trên \( D \) nếu \( f(x) \ge m, \forall x \in D \) và \( \exists x_0 \in D, f(x_0) = m \).
Ký hiệu: \( m = \min_{D} f(x) \).
- Khi nói đến giá trị lớn nhất, giá trị nhỏ nhất của một hàm số thì ta hiểu đó là giá trị lớn nhất, giá trị nhỏ nhất của hàm số đó trên tập xác định của nó.
- Ta có thể tìm giá trị lớn nhất, giá trị nhỏ nhất của một hàm số bằng cách dựa vào đồ thị hoặc dựa vào bảng biến thiên của nó.
Phương pháp tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số
Bài toán: Tìm giá trị lớn nhất – giá trị nhỏ nhất của hàm số \( y = f(x) \) trên \( [a;b] \).
- Bước 1: Tính \( y' = f'(x) \). Tìm các nghiệm \( x_i \in (a;b), i = 1, 2, 3, ... \) mà tại đó đạo hàm bằng 0 hoặc không tồn tại.
- Bước 2: Tính các giá trị \( f(a), f(b) \) và \( f(x_i) \) (nếu có).
- Bước 3: So sánh tất cả giá trị trong bước 2 để kết luận về giá trị lớn nhất, nhỏ nhất của hàm số trên đoạn \( [a;b] \).
- Mọi hàm số liên tục trên đoạn \( [a;b] \) thì chúng đều có giá trị lớn nhất, giá trị nhỏ nhất trên đoạn \( [a;b] \).
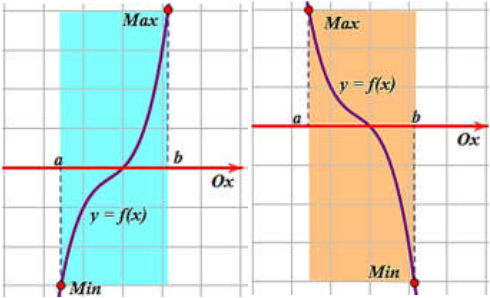
- Nếu hàm số \( y = f(x) \) đồng biến trên đoạn \( [a;b] \) thì \( f(a) \le f(x) \le f(b) \) hay \( \max_{[a;b]}f(x) = f(b) \), \( \min_{[a;b]}f(x) = f(a) \).
- Nếu hàm số \( f(x) \) nghịch biến trên đoạn \( [a;b] \) thì \( f(a) \ge f(x) \ge f(b) \) hay \( \max_{[a;b]}f(x) = f(a) \), \( \min_{[a;b]}f(x) = f(b) \).
- Bước 1: Tính \( y' = f'(x) \). Tìm các nghiệm \( x_i \) mà tại đó đạo hàm bằng 0 hoặc không tồn tại.
- Bước 2: Lập bảng biến thiên của hàm số trên khoảng hoặc nửa khoảng đã cho.
- Bước 3: Dựa vào bảng biến thiên để kết luận về giá trị lớn nhất, giá trị nhỏ nhất của hàm số trên khoảng nửa khoảng cho trước.
CÁC DẠNG TOÁN VÀ PHƯƠNG PHÁP GIẢI
Dạng 1: Tìm GTLN-GTNN của hàm số trên đoạn [a ; b]
Phương pháp giải:
- Bước 0: Tìm tập xác định hàm số (nếu đề bài chưa cho trước đoạn cần tìm max-min).
- Bước 1: Tính đạo hàm \( f'(x) \) và cho \( f'(x) = 0 \) để tìm nghiệm \( x_i \in [a;b], i = 1,2,... \)
- Bước 2: Tính các giá trị \( f(a), f(b), f(x_i) \).
- Bước 3: So sánh các giá trị trong bước 2, kết luận về Max-Min của hàm số trên đoạn \( [a; b] \).
VÍ DỤ MINH HỌA
Ví dụ 1: Tìm GTLN-GTNN của hàm số trên đoạn [0;3]
Dạng 1Giá trị lớn nhất và giá trị nhỏ nhất của hàm số \( y = f(x) = x^3 + 3x^2 - 9x + 1 \) trên đoạn \( [0;3] \) lần lượt bằng bao nhiêu?
Lời giải:
Nhận xét: Hàm số đã cho liên tục trên \( [0;3] \).
Đạo hàm: \( y' = 3x^2 + 6x - 9 \); \( y' = 0 \Leftrightarrow \begin{cases} x = 1 \text{ (nhận)} \\ x = -3 \text{ (loại)} \end{cases} \).
Ta có: \( f(0) = 1, f(1) = -4, f(3) = 28 \). Vậy \( \max_{x \in [0;3]} f(x) = f(3) = 28 \), \( \min_{x \in [0;3]} f(x) = f(1) = -4 \).
Kết luận: Giá trị lớn nhất là 28, giá trị nhỏ nhất là -4.
Ví dụ 2: Tìm GTLN của hàm số trên đoạn [1;2]
Dạng 1Tìm giá trị lớn nhất của hàm số \( y = \frac{2x-1}{x+1} \) trên đoạn \( [1;2] \).
Lời giải:
Nhận xét: Hàm số đã cho liên tục \( \forall x \neq -1 \) nên cũng liên tục trên \( [1;2] \).
Đạo hàm \( y' = \frac{3}{(x+1)^2} > 0, \forall x \in [1;2] \).
Ta có \( y(1) = \frac{1}{2} \), \( y(2) = 1 \). Vậy \( \max_{[1;2]} y = y(2) = 1 \).
Kết luận: Giá trị lớn nhất là 1.
Ví dụ 3: Tìm GTNN của hàm số trên đoạn [0;2]
Dạng 1Tìm giá trị nhỏ nhất của hàm số \( y = \frac{x^2-5}{x+3} \) trên đoạn \( [0;2] \).
Lời giải:
Nhận xét: Hàm số đã cho liên tục \( \forall x \neq -3 \) nên cũng liên tục trên \( [0;2] \).
Đạo hàm: \( y' = \frac{x^2 + 6x + 5}{(x+3)^2} \); \( y' = 0 \Leftrightarrow \begin{cases} x = -1 \text{ (loại)} \\ x = -5 \text{ (loại)} \end{cases} \).
Ta có: \( y(0) = -\frac{5}{3} \), \( y(2) = -\frac{1}{3} \). Vậy \( \min_{[0;2]} y = y(0) = -\frac{5}{3} \).
Kết luận: Giá trị nhỏ nhất là \( -\frac{5}{3} \).
Ví dụ 4: Tìm GTLN-GTNN của hàm số trên tập xác định
Dạng 1Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số \( f(x) = \sqrt{2-x^2} + x \).
Lời giải:
Điều kiện xác định: \( 2 - x^2 \ge 0 \Leftrightarrow -\sqrt{2} \le x \le \sqrt{2} \). Tập xác định: \( D = [-\sqrt{2}; \sqrt{2}] \).
Đạo hàm: \( y' = \frac{-x}{\sqrt{2-x^2}} + 1 \).
\( y' = 0 \Leftrightarrow \sqrt{2-x^2} = x \Leftrightarrow \begin{cases} x \ge 0 \\ 2 - x^2 = x^2 \end{cases} \Leftrightarrow x = 1 \in D \).
Ta có: \( y(-\sqrt{2}) = -\sqrt{2} \), \( y(1) = 2 \), \( y(\sqrt{2}) = \sqrt{2} \).
Vậy \( \min_D y = -\sqrt{2} \), \( \max_D y = 2 \).
Kết luận: Giá trị lớn nhất là 2, giá trị nhỏ nhất là \( -\sqrt{2} \).
Dạng 2: Tìm Max-Min của hàm số trên một khoảng, nửa khoảng
Phương pháp giải:
- Bước 0: Tìm tập xác định (nếu đề bài chưa cho trước khoảng, nửa khoảng cần tìm max-min).
- Bước 1: Tìm đạo hàm của hàm số và tìm nghiệm (nếu có) của đạo hàm đó.
- Bước 2: Lập bảng biến thiên và kết luận về Max-Min hàm số.
Ví dụ 5: Tìm GTNN của hàm số trên khoảng (1;+\infty)
Dạng 2Gọi \( m \) là giá trị nhỏ nhất của hàm số \( y = x - 1 + \frac{4}{x-1} \) trên khoảng \( (1; +\infty) \). Tìm \( m \).
Lời giải:
Tập xác định \( D = \mathbb{R} \setminus \{1\} \).
Ta có \( y' = \frac{x^2 - 2x - 3}{(x-1)^2} \).
\( y' = 0 \Leftrightarrow \begin{cases} x = -1 \\ x = 3 \end{cases} \).
Ta có: \( m = \min_{(1; +\infty)} y = 4 \) khi \( x = 3 \).
Kết luận: Giá trị nhỏ nhất là 4.
Ví dụ 6: Tìm GTLN-GTNN của hàm số trên tập xác định
Dạng 2Mệnh đề nào sau đây là đúng về hàm số \( y = \frac{x+1}{\sqrt{x^2+5}} \) trên tập xác định của nó.
Lời giải:
Tập xác định \( D = \mathbb{R} \).
\( y' = \frac{5 - x}{\sqrt{x^2 + 5}(x^2 + 5)} \).
\( y' = 0 \Leftrightarrow x = 5 \).
Từ bảng biến thiên có \( \max_{\mathbb{R}} y = y(5) = \frac{\sqrt{30}}{5} \) khi \( x = 5 \). Hàm số không có giá trị nhỏ nhất.
Kết luận: Hàm số có giá trị lớn nhất là \( \frac{\sqrt{30}}{5} \) và không có giá trị nhỏ nhất.
Dạng 3: Tìm GTLN-GTNN của hàm số lượng giác, hàm số mũ, hàm số lôgarit
Ví dụ 7: Tìm GTLN-GTNN của hàm số lượng giác trên đoạn [0;π]
Dạng 3Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số \( f(x) = \sin^2 x + \cos x \) trên đoạn \( [0;\pi] \).
Lời giải:
Ta có: \( f'(x) = 2\sin x \cos x - \sin x = \sin x(2\cos x - 1) \).
\( f'(x) = 0 \Leftrightarrow \begin{cases} \sin x = 0 \\ \cos x = \frac{1}{2} \end{cases} \Leftrightarrow x = \frac{\pi}{3} \in (0;\pi) \).
Ta có: \( f(0) = 1 \); \( f\left(\frac{\pi}{3}\right) = \frac{5}{4} \); \( f(\pi) = -1 \).
Vậy \( \max_{[0;\pi]} f(x) = \frac{5}{4} \) và \( \min_{[0;\pi]} f(x) = -1 \).
Kết luận: Giá trị lớn nhất là \( \frac{5}{4} \), giá trị nhỏ nhất là -1.
Ví dụ 8: Tìm GTLN-GTNN của hàm số mũ và lôgarit
Dạng 3Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số:
a) \( y = (x-1)e^{-x} \) trên đoạn \( [-1;1] \).
b) \( y = x \ln x + 1 \) trên đoạn \( \left[\frac{1}{e^2}; e\right] \).
Lời giải:
a) Ta có: \( y' = (2-x)e^{-x} \); \( y' = 0 \Leftrightarrow x = 2 \notin (-1;1) \).
\( y(-1) = -2e \); \( y(1) = 0 \). Vậy \( \max_{[-1;1]} y = 0 \) và \( \min_{[-1;1]} y = -2e \).
b) Ta có: \( y' = \ln x + 1 \); \( y' = 0 \Leftrightarrow x = \frac{1}{e} \in \left(\frac{1}{e^2}; e\right) \).
\( y\left(\frac{1}{e^2}\right) = 1 - \frac{2}{e^2} \); \( y\left(\frac{1}{e}\right) = 1 - \frac{1}{e} \); \( y(e) = e + 1 \).
Vậy \( \max_{\left[\frac{1}{e^2}; e\right]} y = e + 1 \) và \( \min_{\left[\frac{1}{e^2}; e\right]} y = 1 - \frac{1}{e} \).
Kết luận: a) Giá trị lớn nhất là 0, giá trị nhỏ nhất là \( -2e \). b) Giá trị lớn nhất là \( e + 1 \), giá trị nhỏ nhất là \( 1 - \frac{1}{e} \).
Dạng 4: Tìm tham số thỏa mãn điều kiện Max-Min cho trước
Phương pháp giải:
- Bước 0: Tìm tập xác định hàm số (nếu đề bài chưa cho trước đoạn cần tìm max-min).
- Bước 1: Tính đạo hàm \( f'(x) \) và cho \( f'(x) = 0 \) để tìm nghiệm \( x_i \in [a;b], i = 1,2,... \). Nếu \( x_i \) chứa tham số và chưa biết có thuộc \( [a;b] \) hay không thì ta cần xét các trường hợp.
- Bước 2: Tính các giá trị \( f(a), f(b), f(x_i) \).
- Bước 3: So sánh các giá trị trong bước 2 để tìm Max-Min hàm số (theo tham số) rồi cho chúng thỏa mãn đề bài để suy ra tham số cần tìm.
Ví dụ 9: Tìm tham số m để GTNN bằng 0
Dạng 4Tìm giá trị của \( m \) để hàm số \( y = -x^3 - 3x^2 + m \) có giá trị nhỏ nhất trên \( [-1;1] \) bằng 0.
Lời giải:
Đạo hàm: \( y' = -3x^2 - 6x = -3x(x+2) \); \( y' = 0 \Leftrightarrow \begin{cases} x = 0 \text{ (nhận)} \\ x = -2 \text{ (loại)} \end{cases} \).
Ta có: \( y(-1) = m - 2 \), \( y(0) = m \), \( y(1) = m - 4 \).
Dễ thấy \( \min_{[-1;1]} y = y(1) = m - 4 \). Theo đề: \( m - 4 = 0 \Leftrightarrow m = 4 \).
Kết luận: Giá trị của \( m \) là 4.
Ví dụ 10: Tìm tham số m để GTNN bằng -1
Dạng 4Hàm số \( y = \frac{x - m^2}{x + 1} \) có giá trị nhỏ nhất trên đoạn \( [0;1] \) bằng -1 khi:
Lời giải:
Hàm số đã cho xác định với mọi \( x \neq -1 \) nên cũng xác định trên \( [0;1] \).
Đạo hàm: \( y' = \frac{1 + m^2}{(x+1)^2} > 0, \forall x \in [0;1] \Rightarrow \) Hàm số đã cho đồng biến trên \( [0;1] \).
Ta có: \( \min_{[0;1]} f(x) = f(0) = -m^2 \); theo đề: \( -m^2 = -1 \Leftrightarrow m = \pm 1 \).
Kết luận: Giá trị của \( m \) là \( \pm 1 \).
Ví dụ 11: Tìm tham số m để GTNN bằng 3
Dạng 4Cho hàm số \( y = \frac{x + m}{x - 1} \) (\( m \) là tham số thực) thỏa mãn \( \min_{[2;4]} y = 3 \). Mệnh đề nào dưới đây là đúng?
Lời giải:
Hàm số liên tục trên đoạn \( [2;4] \).
Ta có: \( y' = \frac{-1 - m}{(x-1)^2} \). Nếu \( m = -1 \) thì hàm số đã cho là hàm hằng \( y = 1, \forall x \neq 1 \), không tồn tại \( \min_{[2;4]} y = 3 \).
Trường hợp 1: \( y(2) > y(4) \Rightarrow \min_{[2;4]} y = y(4) = 3 \Leftrightarrow \frac{4 + m}{4 - 1} = 3 \Rightarrow m = 5 \).
Trường hợp 2: \( y(2) < y(4) \Rightarrow \min_{[2;4]} y = y(2) = 3 \Leftrightarrow \frac{2 + m}{2 - 1} = 3 \Rightarrow m = 1 \).
Kết luận: Giá trị của \( m \) là 1 hoặc 5.
Ví dụ 12: Tìm tham số m để GTLN bằng \( 3\sqrt{2} \)
Dạng 4Biết rằng giá trị lớn nhất của hàm số \( y = x + \sqrt{4 - x^2} + m \) là \( 3\sqrt{2} \). Giá trị của \( m \) là:
Lời giải:
Hàm số xác định \( \Leftrightarrow 4 - x^2 \ge 0 \Leftrightarrow x \in [-2;2] \).
Đạo hàm: \( y' = 1 - \frac{x}{\sqrt{4 - x^2}} = \frac{\sqrt{4 - x^2} - x}{\sqrt{4 - x^2}} \); \( y' = 0 \Leftrightarrow \sqrt{4 - x^2} = x \Leftrightarrow x = \sqrt{2} \).
Ta có: \( y(-2) = m - 2 \), \( y(\sqrt{2}) = m + 2\sqrt{2} \), \( y(2) = m + 2 \).
Do đó \( \max_D y = m + 2\sqrt{2} = 3\sqrt{2} \Leftrightarrow m = \sqrt{2} \).
Kết luận: Giá trị của \( m \) là \( \sqrt{2} \).
Ví dụ 13: Tìm tham số m để GTNN bé hơn 3
Dạng 4Tìm tất cả các giá trị của \( m > 0 \) để giá trị nhỏ nhất của hàm số \( y = x^3 - 3x + 1 \) trên đoạn \( [m+1; m+2] \) luôn bé hơn 3.
Lời giải:
Ta có \( y' = 3x^2 - 3 \), \( y' = 0 \Leftrightarrow x = \pm 1 \). \( y_{CT} = y(1) = -1 \) và \( y_{CĐ} = y(-1) = 3 \).
Ta có \( m > 0 \Rightarrow m + 1 > 1 \); do đó trên đoạn \( [m+1; m+2] \) hàm số luôn đồng biến.
Khi đó GTNN: \( \min_{[m+1; m+2]} y = y(m+1) = (m+1)^3 - 3(m+1) + 1 \).
GTNN luôn bé hơn 3 \( \Leftrightarrow (m+1)^3 - 3(m+1) - 2 < 0 \Leftrightarrow \begin{cases} m + 1 < 2 \\ m + 1 \neq -1 \end{cases} \Leftrightarrow \begin{cases} m < 1 \\ m \neq -2 \end{cases} \).
Kết hợp điều kiện \( m > 0 \) ta được \( m \in (0;1) \).
Kết luận: Giá trị của \( m \) thuộc \( (0;1) \).
Dạng 5: Tìm Max-Min cho bài toán thực tế
Phương pháp giải:
- Bước 1: Lập ra hàm số \( y = f(x) \) là hàm đặc trưng cho chi phí, lợi nhuận, quãng đường, diện tích, thể tích v.v...
- Bước 2: Khảo sát và tìm giá trị lớn nhất (hay nhỏ nhất) của hàm số này tùy vào yêu cầu bài toán.
Công thức cho Bài toán Chuyển động:
- Một vật chuyển động với quãng đường được tính theo công thức \( S(t) \) (với \( t \) là thời gian), vật đó có vận tốc: \( v(t) = S'(t) \).
- Một vật chuyển động với vận tốc \( v(t) \) sẽ có gia tốc là \( a(t) = v'(t) \).
Ví dụ 14: Tối ưu thể tích hộp không nắp
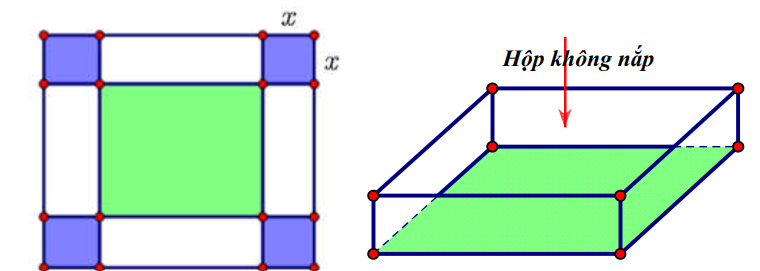
Dạng 5Cho một tấm nhôm hình vuông cạnh 12 cm. Người ta cắt ở bốn góc của tấm nhôm đó bốn hình vuông bằng nhau, mỗi hình vuông có cạnh bằng \( x \) (cm), rồi gập tấm nhôm lại để được một cái hộp không nắp. Tìm \( x \) để hộp nhận được có thể tích lớn nhất.
Lời giải:
Ta nhận thấy cạnh hình vuông nhỏ là \( x \) (cm), \( 0 < x < 6 \) chính là chiều cao của hình hộp chữ nhật được tạo thành.
Sau khi cắt bỏ đi các hình vuông nhỏ cạnh \( x \) thì đáy khối hộp không nắp là một hình vuông có cạnh \( 12 - 2x \) (cm).
Thể tích khối hộp là hàm số: \( V(x) = (12 - 2x)^2 \cdot x = 4x^3 - 48x^2 + 144x \) với \( 0 < x < 6 \).
\( V'(x) = 12x^2 - 96x + 144 = 0 \Leftrightarrow \begin{cases} x = 6 \text{ (loại)} \\ x = 2 \text{ (nhận)} \end{cases} \).
Thể tích khối hộp lớn nhất là \( \max_{(0;6)} V = V(2) = 128 (\text{cm}^3) \); khi đó cạnh hình vuông nhỏ là \( x = 2 (\text{cm}) \).
Kết luận: Giá trị \( x = 2 \) cm để thể tích lớn nhất là 128 cm³.
Ví dụ 15: Tối ưu chi phí xây bể chứa nước
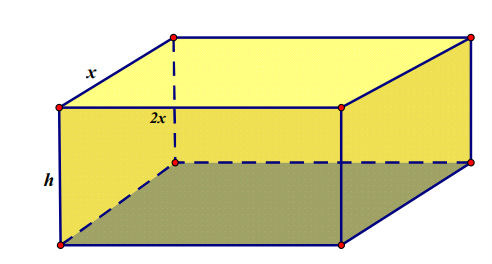
Dạng 5Một người muốn xây một cái bể chứa nước, dạng một khối hộp chữ nhật không nắp có thể tích bằng 288 dm³. Đáy bể là hình chữ nhật có chiều dài gấp đôi chiều rộng, giá thuê nhân công để xây bể là 500000 đồng/m². Nếu người đó biết xác định các kích thước của bể hợp lí thì chi phí thuê nhân công sẽ thấp nhất. Hỏi người đó trả chi phí thấp nhất để thuê nhân công xây dựng bể đó là bao nhiêu?
Lời giải:
Gọi \( x \) là chiều rộng của đáy bể (\( x > 0 \)). Khi đó chiều dài đáy bể là \( 2x \).
Thể tích của bể: \( V = 288 \text{ dm}^3 = 0.288 \text{ m}^3 \).
Mà \( V = x \cdot 2x \cdot h \Rightarrow h = \frac{V}{2x^2} = \frac{0.288}{2x^2} = \frac{0.144}{x^2} \).
Phần xây dựng của bể (trừ mặt trên của bể) có diện tích:
\( S = 2 \cdot h \cdot x + 2 \cdot h \cdot 2x + x \cdot 2x = 6hx + 2x^2 = 6 \cdot \frac{0.144}{x^2} \cdot x + 2x^2 = \frac{0.864}{x} + 2x^2, x > 0 \).
Xét hàm số \( S(x) = \frac{0.864}{x} + 2x^2 \); \( S'(x) = -\frac{0.864}{x^2} + 4x = \frac{4x^3 - 0.864}{x^2} \).
\( S'(x) = 0 \Leftrightarrow 4x^3 - 0.864 = 0 \Leftrightarrow x = \sqrt[3]{\frac{0.864}{4}} = 0.6 \).
Ta có: \( \min_{(0; +\infty)} S(x) = \frac{54}{25} \text{ m}^2 \), nên chi phí thấp nhất phải trả: \( \frac{54}{25} \cdot 500000 = 1080000 \) đồng.
Kết luận: Chi phí thấp nhất là 1080000 đồng.
Ví dụ 16: Tìm vận tốc lớn nhất
Dạng 5Một vật chuyển động dọc theo trục Ox mà vị trí của nó là \( s \) (mét) được cho bởi công thức \( s = -\frac{1}{2}t^3 + 9t^2 \), với \( t \) (giây) là khoảng thời gian tính từ lúc vật bắt đầu chuyển động. Hỏi trong khoảng thời gian 10 giây kể từ lúc bắt đầu chuyển động, vận tốc lớn nhất mà vật đạt được bằng bao nhiêu?
Lời giải:
Vận tốc chuyển động của vật: \( v(t) = s'(t) = -\frac{3}{2}t^2 + 18t \).
Xét hàm \( v(t) = -\frac{3}{2}t^2 + 18t \) với \( t \in (0;10) \); \( v'(t) = -3t + 18 \); \( v'(t) = 0 \Leftrightarrow t = 6 \).
Dựa vào bảng biến thiên, ta thấy vận tốc lớn nhất của vật trong khoảng 10 giây đầu là 54 m/s.
Kết luận: Vận tốc lớn nhất là 54 m/s.
Ví dụ 17: Tối ưu quãng đường qua cầu
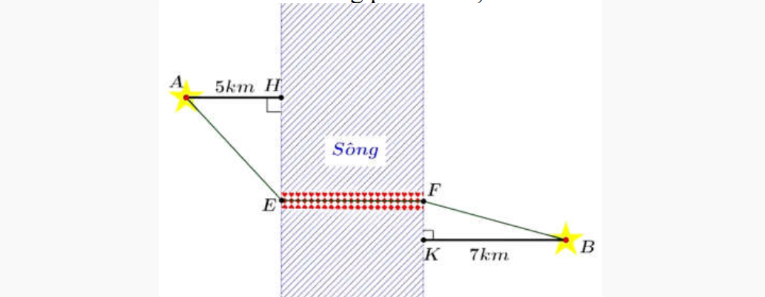
Dạng 5Hai thành phố cách nhau một con sông. Lấy \( A \) và \( B \) lần lượt là hai điểm mốc của hai thành phố trong việc đo đạc, đơn vị là km. Người ta xây dựng một cây cầu \( EF \) bắc qua sông biết rằng vị trí \( A \) cách con sông một khoảng là 5 km và vị trí \( B \) cách con sông một khoảng là 7 km, biết \( HE + KF = 24 \) km và độ dài \( EF \) không đổi. Hỏi người ta cần xây cây cầu cách vị trí \( B \) là bao nhiêu km để đường đi từ vị trí \( A \) đến vị trí \( B \) là ngắn nhất (đi theo đường gấp khúc \( AEFB \))? (Kết quả gần đúng được làm tròn đến hàng phần trăm).
Lời giải:
Đặt \( HE = x \Rightarrow FK = 24 - x \) (\( 0 < x < 24 \)). Ta có:
\( AE = \sqrt{25 + x^2} \)
\( BF = \sqrt{49 + (24 - x)^2} \)
Ta cần tổng quãng đường \( AE + EF + FB \) ngắn nhất, mà \( EF \) không đổi nên \( AE + FB \) bé nhất.
Xét hàm số \( f(x) = \sqrt{x^2 + 25} + \sqrt{x^2 - 48x + 625} \);
\( f'(x) = \frac{x}{\sqrt{x^2 + 25}} + \frac{x - 24}{\sqrt{x^2 - 48x + 625}} \), \( \forall x \in (0;24) \); \( f'(x) = 0 \Rightarrow x = 10 \).
Ta có: \( \min_{(0;24)} f(x) = 12\sqrt{5} \); khi đó \( x = 10 \) km và \( BF = 7\sqrt{5} \text{ km} \approx 15.65 \text{ km} \).
Kết luận: Cây cầu cần xây cách vị trí \( B \) là 15.65 km.
Ví dụ 18: Tối ưu chiều dài thang
Dạng 5Một bức tường cao 2m nằm song song với bức tường của một tòa nhà và cách tòa nhà đó 2m. Người ta muốn làm ra một chiếc thang bắc từ mặt đất bên ngoài bức tường, gác qua bức tường và chạm vào tòa nhà. Hỏi chiều dài tối thiểu của thang bằng bao nhiêu mét?
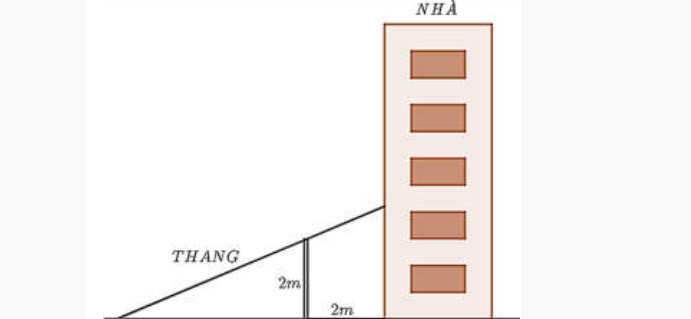
Lời giải:
Xét hệ điểm \( A, B, C, D, E \) như hình vẽ.
Gọi \( BC = x (x > 0) \). Ta cần tìm \( x \) để độ dài \( CD \) đạt giá trị nhỏ nhất.
Dễ thấy hai tam giác \( CAB, CDE \) đồng dạng, suy ra: \( \frac{BC}{CE} = \frac{AC}{CD} \Rightarrow CD = AC \cdot \frac{x + 2}{x} \).
Đặt \( f(x) = \sqrt{x^2 + 4} \cdot \frac{x + 2}{x} \) với \( x > 0 \).
\( f'(x) = \frac{x}{\sqrt{x^2 + 4}} \cdot \frac{x + 2}{x} - \sqrt{x^2 + 4} \cdot \frac{2}{x^2} = \frac{x^2(x + 2) - 2(x^2 + 4)}{x^2 \sqrt{x^2 + 4}} = 0 \)
\( \Leftrightarrow x^3(x + 2) = 2(x^2 + 4) \Leftrightarrow x^3 = 8 \Leftrightarrow x = 2 \).
Bảng biến thiên của \( f(x) \):
Vậy chiều dài tối thiểu của thang bằng \( 4\sqrt{2} \).
Kết luận: Chiều dài tối thiểu của thang là \( 4\sqrt{2} \) mét.
Ví dụ 19: Tối ưu thể tích khối trụ nội tiếp elip
Dạng 5Một quả trứng khủng long đồ chơi bằng nhựa có thiết diện qua trục lớn là một đường elip. Biết độ dài mỗi trục là 12 cm và 8 cm. Bên trong quả trứng người ta cần thiết kế một chiếc hộp hình trụ để đựng các đồ chơi trẻ con như bóng đèn xanh đỏ, kẹo v.v... Hỏi khối trụ như thế có thể tích tối đa bao nhiêu cm³ (làm tròn đến hàng đơn vị).
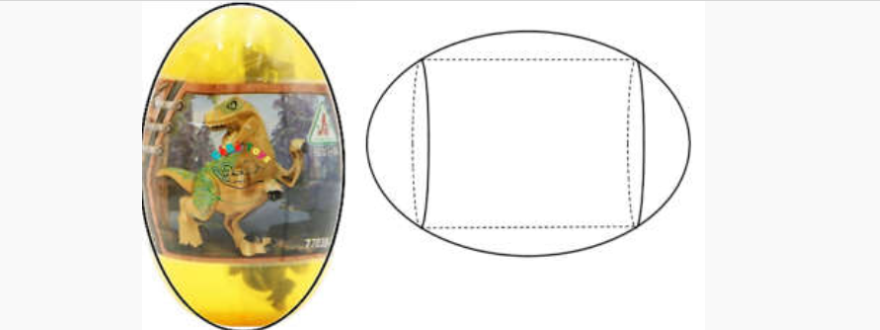
Lời giải:
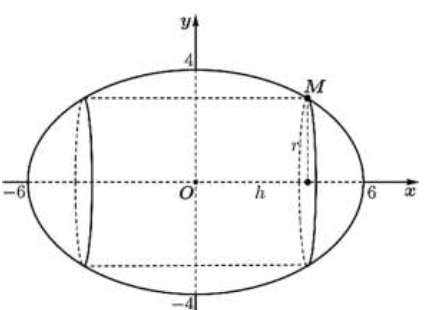
Gắn elip lên hệ trục tọa độ Oxy như hình vẽ, elip có \( 2a = 12 \Rightarrow a = 6 \); \( 2b = 8 \Rightarrow b = 4 \).
Phương trình chính tắc elip (E): \( \frac{x^2}{36} + \frac{y^2}{16} = 1 \).
Đặt chiều cao và bán kính đáy hình trụ nội tiếp elip là \( h, r \) thì điểm tiếp xúc \( M\left(\frac{h}{2}; r\right) \) với \( 0 < h < 12 \); \( 0 < r < 4 \).
Điểm \( M \) thuộc (E): \( \frac{(h/2)^2}{36} + \frac{r^2}{16} = 1 \Rightarrow \frac{h^2}{144} + \frac{r^2}{16} = 1 \Rightarrow r^2 = 16\left(1 - \frac{h^2}{144}\right) \).
Thể tích khối trụ là \( V = \pi r^2 h = \pi 16 \left(1 - \frac{h^2}{144}\right) h = \pi \left(16h - \frac{h^3}{9}\right) \).
Ta có \( V' = \pi \left(16 - \frac{h^2}{3}\right) \); \( V' = 0 \Rightarrow 16 - \frac{h^2}{3} = 0 \Rightarrow h^2 = 48 \Rightarrow h = 4\sqrt{3} \in (0;12) \).
Giá trị lớn nhất của thể tích khối trụ là \( V_{\max} = V(4\sqrt{3}) = \pi \left(16 \cdot 4\sqrt{3} - \frac{(4\sqrt{3})^3}{9}\right) \approx 232 \text{ cm}^3 \).
Kết luận: Thể tích tối đa của khối trụ là 232 cm³.
