TÓM TẮT LÍ THUYẾT
ĐƯỜNG TIỆM CẬN ĐỨNG
Định Nghĩa
Đường thẳng \( x = x_0 \) (\( x_0 \) là hằng số) được gọi là một đường tiệm cận đứng (hay tiệm cận đứng) của đồ thị hàm số \( y = f(x) \) nếu một trong bốn điều kiện sau được thỏa mãn:
- \( \lim_{x \to x_0^+} f(x) = +\infty \);
- \( \lim_{x \to x_0^+} f(x) = -\infty \);
- \( \lim_{x \to x_0^-} f(x) = +\infty \);
- \( \lim_{x \to x_0^-} f(x) = -\infty \).
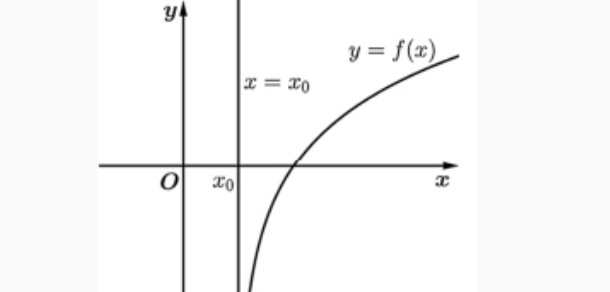
Mỗi đồ thị hàm số có thể không có tiệm cận đứng, cũng có thể có một hoặc nhiều tiệm cận đứng.
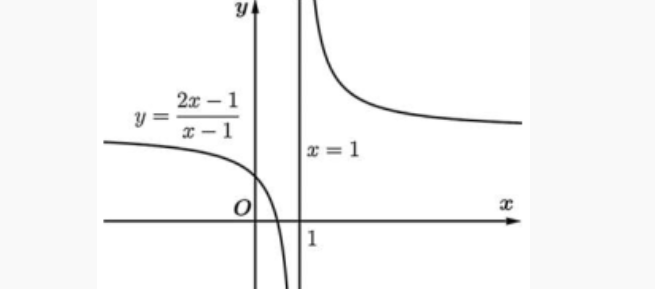
Hình vẽ dưới đây biểu diễn đường tiệm cận đứng \( x=1 \) của đồ thị hàm số \( y=\frac{2x-1}{x-1} \).
ĐƯỜNG TIỆM CẬN NGANG
Định Nghĩa
Đường thẳng \( y = y_0 \) (\( y_0 \) là hằng số) được gọi là đường tiệm cận ngang (hay tiệm cận ngang) của đồ thị hàm số \( y=f(x) \) nếu một trong hai điều kiện sau được thỏa mãn:
- \( \lim_{x \to +\infty} f(x) = y_0 \);
- \( \lim_{x \to -\infty} f(x) = y_0 \).
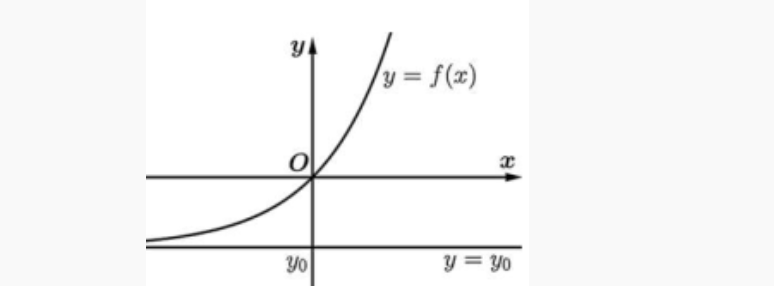
Mỗi đồ thị hàm số có tối đa hai đường tiệm cận ngang.
Khi tìm tiệm cận ngang của một đồ thị hàm số dạng phân thức \( y=\frac{P(x)}{Q(x)} \), ta cần tính giới hạn hàm số khi \( x \) dần về vô cùng, kết quả thu được sẽ rơi vào ba trường hợp sau:
- Trường hợp 1: Nếu bậc \( P(x) \) < bậc \( Q(x) \) thì \( \lim_{x \to \pm\infty} y = \lim_{x \to \pm\infty} \frac{P(x)}{Q(x)} = 0 \). Tiệm cận ngang của đồ thị hàm số là đường thẳng \( y=0 \) (trục Ox).
- Trường hợp 2: Nếu bậc \( P(x) \) = bậc \( Q(x) \) thì \( \lim_{x \to \pm\infty} y = \lim_{x \to \pm\infty} \frac{P(x)}{Q(x)} = \frac{a}{b} \), trong đó a là hệ số của bậc cao nhất tử số, b là hệ số của bậc cao nhất mẫu số. Tiệm cận ngang của đồ thị hàm số là đường thẳng \( y = \frac{a}{b} \).
- Trường hợp 3: Nếu bậc \( P(x) \) > bậc \( Q(x) \) thì \( \lim_{x \to \pm\infty} y = \lim_{x \to \pm\infty} \frac{P(x)}{Q(x)} = \infty \) (tùy dấu \( +\infty \) hay \( -\infty \)). Đồ thị hàm số không có tiệm cận ngang.
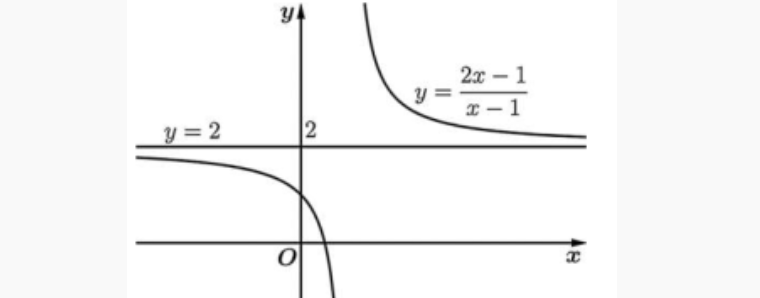
Hình vẽ dưới đây biểu diễn đường tiệm cận ngang \( y=2 \) của đồ thị hàm số \( y=\frac{2x-1}{x-1} \).
ĐƯỜNG TIỆM CẬN XIÊN
Định Nghĩa
Đường thẳng \( y=ax+b \) (\( a \ne 0 \)) được gọi là đường tiệm cận xiên (hay tiệm cận xiên) của đồ thị hàm số \( y=f(x) \) nếu một trong hai điều kiện sau được thỏa mãn:
- \( \lim_{x \to +\infty} [f(x)-(ax+b)] = 0 \);
- \( \lim_{x \to -\infty} [f(x)-(ax+b)] = 0 \).
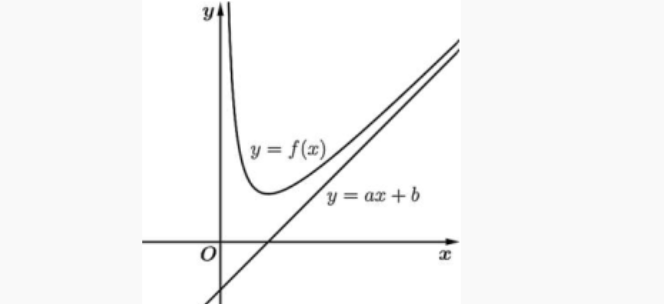
Trong trường hợp tổng quát, ta có thể tìm phương trình đường tiệm cận xiên \( y=ax+b \) của đồ thị hàm số \( y=f(x) \) theo công thức sau:
\( a = \lim_{x \to +\infty} \frac{f(x)}{x} \), \( b = \lim_{x \to +\infty} [f(x)-ax] \)
hoặc \( a = \lim_{x \to -\infty} \frac{f(x)}{x} \), \( b = \lim_{x \to -\infty} [f(x)-ax] \).
Nếu \( a=0 \) thì đồ thị hàm số không có tiệm cận xiên mà có tiệm cận ngang là \( y=b \).
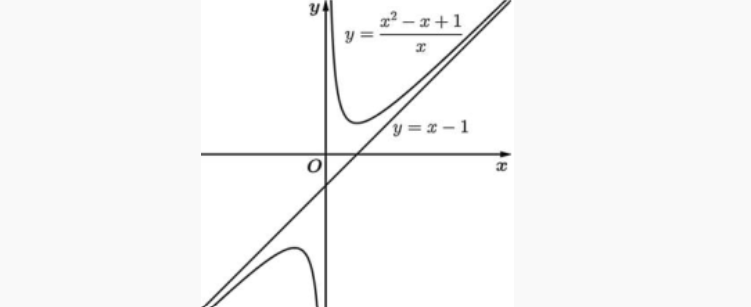
Hình vẽ dưới đây biểu diễn đường tiệm cận xiên \( y=x-1 \) của đồ thị hàm số \( y = \frac{x^2-x+1}{x} \).
- Đồ thị hàm số \( y=\frac{ax+b}{cx+d} \) có tiệm cận khi và chỉ khi \( \begin{cases} c \ne 0 \\ ad-bc \ne 0 \end{cases} \).
- Nếu đồ thị hàm số \( y=\frac{ax+b}{cx+d} \) có tiệm cận thì phương trình tiệm cận đứng là \( x=-\frac{d}{c} \) và phương trình tiệm cận ngang là \( y=\frac{a}{c} \).
- Nếu hàm số có dạng \( y=ax+b+\frac{c}{dx+e} \) (\( acd \ne 0 \)) thì đường thẳng \( y=ax+b \) là tiệm cận xiên của đồ thị hàm số.
VÍ DỤ MINH HỌA
Ví dụ 1: Tìm tiệm cận đứng
Tiệm cận đứngTìm tiệm cận đứng của các đồ thị hàm số sau:
a) \( y=\frac{1}{x(x-1)} \);
b) \( y=\frac{x+3}{\sqrt{x-2}} \)
Lời giải:
a) Tập xác định: \( D = \mathbb{R} \setminus \{0; 1\} \).
Ta có: \( \lim_{x \to 0^+} y = -\infty \) (tương tự: \( \lim_{x \to 0^-} y = +\infty \)). Suy ra đường thẳng \( x=0 \) là một tiệm cận đứng của đồ thị hàm số.
Ta có: \( \lim_{x \to 1^+} y = +\infty \) (tương tự: \( \lim_{x \to 1^-} y = -\infty \)). Suy ra đường thẳng \( x=1 \) là một tiệm cận đứng của đồ thị hàm số.
b) Tập xác định: \( D = (2; +\infty) \).
Ta có: \( \lim_{x \to 2^+} y = +\infty \) nên \( x=2 \) là một đường tiệm cận đứng của đồ thị hàm số.
Lưu ý: Khi tìm tiệm cận đứng của đồ thị hàm số, nếu giới hạn một bên của hàm số cho ta kết quả vô cùng (\( +\infty \) hoặc \( -\infty \)) thì ta không cần tính giới hạn bên còn lại mà vẫn kết luận về đường tiệm cận đứng của đồ thị hàm số.
Kết luận: Đường tiệm cận đứng là \( x=0 \) và \( x=1 \) (đối với a); \( x=2 \) (đối với b).
Ví dụ 2: Tìm tiệm cận đứng
Tiệm cận đứngTìm tiệm cận đứng của các đồ thị hàm số sau:
a) \( y=\frac{x^2-4}{x^2-3x+2} \);
b) \( y=\frac{\sqrt{2-x}}{x^2-2x-3} \)
Lời giải:
a) Tập xác định: \( D = \mathbb{R} \setminus \{1; 2\} \).
Vì \( y = \frac{(x+2)(x-2)}{(x-1)(x-2)} = \frac{x+2}{x-1} \) và \( \lim_{x \to 1^+} y = +\infty \) (tương tự: \( \lim_{x \to 1^-} y = -\infty \)) nên đường thẳng \( x=1 \) là một tiệm cận đứng của đồ thị hàm số.
b) Hàm số xác định khi và chỉ khi \( \begin{cases} 2-x \ge 0 \\ x^2-2x-3 \ne 0 \end{cases} \Leftrightarrow \begin{cases} x \le 2 \\ x \ne -1 \end{cases} \).
Vì \( \lim_{x \to -1^+} y = -\infty \) (tương tự: \( \lim_{x \to -1^-} y = +\infty \)) nên đường thẳng \( x=-1 \) là một tiệm cận đứng của đồ thị hàm số.
Kết luận: Đường tiệm cận đứng là \( x=1 \) (đối với a); \( x=-1 \) (đối với b).
PHÂN DẠNG BÀI TẬP
TÌM TIỆM CẬN CỦA ĐỒ THỊ HÀM PHÂN THỨC ĐẠI SỐ
Phương pháp tìm tiệm cận ngang:
- Cách giải 1:
- Nếu bậc tử < bậc mẫu thì \( \lim_{x \to \pm\infty} y = 0 \) nên đồ thị có tiệm cận ngang \( y=0 \).
- Nếu bậc tử = bậc mẫu thì \( \lim_{x \to \pm\infty} y = \frac{\text{Hệ số lũy thừa cao nhất của tử}}{\text{Hệ số lũy thừa cao nhất của mẫu}} = y_0 \) nên đồ thị có đường tiệm cận ngang là \( y=y_0 \).
- Nếu bậc tử > bậc mẫu thì \( \lim_{x \to \pm\infty} y = \infty \) nên đồ thị không có tiệm cận ngang.
- Cách giải 2:
- Tính các giới hạn hàm số tại âm, dương vô cực và kết luận về tiệm cận ngang của đồ thị hàm số.
- Có thể tham khảo thêm việc sử dụng máy tính cầm tay để tìm các \( \lim_{x \to \pm\infty} y \) như sau: Nhập hàm số và máy và nhấn CALC \( \to 10^{10} \to = \) (ứng với \( \lim_{x \to +\infty} y \)) và nhấn tiếp CALC \( \to -10^{10} \to = \) (ứng với \( \lim_{x \to -\infty} y \)).
So sánh bậc tử và bậc mẫu của hàm phân thức hữu tỉ, ta làm như sau:
Phương pháp tìm tiệm cận đứng:
- Bước 1: Rút gọn phân thức đại số (nếu có thể).
- Bước 2: Tìm tiệm cận đứng của đồ thị bằng cách cho mẫu số bằng 0 và tìm nghiệm (không cần thử lại).
Lưu ý:
- Đồ thị hàm số \( y=\frac{ax+b}{cx+d} \) có tiệm cận khi và chỉ khi \( \begin{cases} c \ne 0 \\ ad-bc \ne 0 \end{cases} \).
- Khi hàm số \( y=\frac{ax+b}{cx+d} \) đã thỏa mãn (*) thì đồ thị hàm số có tiệm cận ngang \( y=\frac{a}{c} \) và tiệm cận đứng \( x=-\frac{d}{c} \). Tâm đối xứng của đồ thị là \( I(-\frac{d}{c}; \frac{a}{c}) \).
Ví dụ 1: Tìm tiệm cận đứng và ngang
Tiệm cậnĐồ thị hàm số \( y=\frac{1-3x}{x+2} \) có các đường tiệm cận đứng và tiệm cận ngang lần lượt là:
A. \( x=-2 \) và \( y=-3 \). B. \( x=-2 \) và \( y=1 \). C. \( x=-2 \) và \( y=3 \). D. \( x=2 \) và \( y=1 \).
Lời giải:
Tiệm cận đứng đồ thị hàm số: \( x = -\frac{d}{c} = \frac{-2}{1} = -2 \).
Tiệm cận ngang đồ thị hàm số: \( y = \frac{a}{c} = \frac{-3}{1} = -3 \).
Kết luận: Đáp án A.
Ví dụ 2: Tìm tiệm cận và tính biểu thức
Tiệm cậnCho hàm số \( y=\frac{-3x+5}{-2x+1} \) có đồ thị (C). Biết rằng (C) có các đường tiệm cận đứng là \( x=m \) và tiệm cận ngang là \( y=n \). Tính biểu thức \( T=m^2+n^2 \).
A. \( \frac{13}{4} \). B. \( \frac{5}{4} \). C. \( \frac{17}{4} \). D. \( \frac{5}{2} \).
Lời giải:
Vậy tiệm cận đứng của đồ thị: \( x = -\frac{d}{c} = \frac{1}{2} \), tiệm cận ngang của đồ thị: \( y = \frac{a}{c} = \frac{3}{2} \).
Do đó \( T = m^2+n^2 = (\frac{1}{2})^2 + (\frac{3}{2})^2 = \frac{5}{2} \).
Kết luận: Đáp án D.
Ví dụ 3: Số đường tiệm cận
Tiệm cậnSố đường tiệm cận của đồ thị hàm số \( y=\frac{2x-1}{x^2-3x+2} \) là
A. 2. B. 3. C. 1. D. 0.
Lời giải:
Nhận xét:
- Hàm số phân thức trên đã được rút gọn (chuẩn thức) nên ta chỉ cần cho mẫu số bằng 0 để tìm các nghiệm \( x_i \) (nếu có), các nghiệm này chính là các đường tiệm cận đứng của đồ thị.
- Mặt khác vì bậc tử (bậc I) bé hơn bậc mẫu (bậc II) nên đồ thị luôn có tiệm cận ngang \( y=0 \).
Xét mẫu bằng 0, ta có: \( x^2-3x+2=0 \Leftrightarrow \begin{cases} x=1 \\ x=2 \end{cases} \). Tiệm cận đứng đồ thị: \( x=1, x=2 \).
Mặt khác: \( \lim_{x \to \pm\infty} y = \lim_{x \to \pm\infty} \frac{2x-1}{x^2-3x+2} = \lim_{x \to \pm\infty} \frac{x^2(\frac{2}{x}-\frac{1}{x^2})}{x^2(1-\frac{3}{x}+\frac{2}{x^2})} = \frac{0}{1} = 0 \). Tiệm cận ngang đồ thị: \( y=0 \).
Kết luận: Đáp án B (3 tiệm cận).
Ví dụ 4: Chọn mệnh đề đúng
Tiệm cậnCho hàm số \( y=\frac{2x^2-x-6}{x^2-4} \) (1). Chọn mệnh đề đúng trong các mệnh đề sau:
A. Đồ thị hàm số (1) có hai tiệm cận đứng và không có tiệm cận ngang.
B. Đồ thị hàm số (1) có hai tiệm cận đứng là \( x=2, x=-2 \).
C. Đồ thị hàm số (1) có tất cả ba tiệm cận.
D. Đồ thị hàm số (1) có một tiệm cận đứng và một tiệm cận ngang.
Lời giải:
Nhận xét:
- Ta thấy nghiệm của mẫu \( \{\pm 2\} \) và nghiệm của tử \( \{2; -\frac{3}{2}\} \) có số 2 là phần tử chung nên hàm số đã cho chưa được chuẩn thức. Ta cần rút gọn trước khi tìm tiệm cận đứng.
- Bậc tử và bậc mẫu của phân thức là bằng nhau (cùng bậc II) nên tiệm cận ngang của đồ thị là \( y=\frac{2}{1}=2 \).
Ta có: \( y = \frac{2x^2-x-6}{x^2-4} = \frac{(x-2)(2x+3)}{(x-2)(x+2)} = \frac{2x+3}{x+2} \) nên đồ thị hàm số có tiệm cận đứng và tiệm cận ngang lần lượt là \( x=-2, y=2 \).
Kết luận: Đáp án D.
Ví dụ 5: Số tiệm cận
Tiệm cậnĐồ thị hàm số \( y=\frac{x^2+2x-3}{(x+3)(x^3-x^2+x-1)} \) có tất cả bao nhiêu tiệm cận đứng và ngang?
A. 2. B. 3. C. 4. D. 1.
Lời giải:
Ta có: \( y=\frac{x^2+2x-3}{(x+3)(x^3-x^2+x-1)} = \frac{(x-1)(x+3)}{(x+3)(x-1)(x^2+1)} = \frac{1}{x^2+1} \).
Xét mẫu số bằng 0 thì \( x^2+1=0 \) (vô nghiệm). Vậy đồ thị hàm số không có tiệm cận đứng.
Vì bậc tử bé hơn bậc mẫu nên \( \lim_{x \to \pm\infty} y = 0 \); suy ra tiệm cận ngang của đồ thị là \( y=0 \).
Kết luận: Đáp án D (1 tiệm cận).
TÌM TIỆM CẬN CỦA ĐỒ THỊ HÀM SỐ CÓ CHỨA CĂN
Phương pháp tìm tiệm cận ngang:
- Tính các giới hạn \( \lim_{x \to +\infty} y \) và \( \lim_{x \to -\infty} y \) để tìm tiệm cận ngang của đồ thị hàm số (nếu có).
Phương pháp tìm tiệm cận đứng:
- Bước 1: Cho mẫu bằng 0 và giải tìm nghiệm \( x_i \) của mẫu (nếu có).
- Bước 2: Kiểm tra xem có nghiệm \( x_i \) nào của mẫu có trùng với nghiệm tử hay không bằng cách thay lần lượt các nghiệm \( x_i \) vào tử số xem tử có bằng 0 hay không.
- Trường hợp 1: Không có nghiệm \( x_i \) nào làm cho tử bằng 0.
- Nếu thay \( x_i \) vào làm cho tử khác 0 thì kết luận \( x=x_i \) là một đường tiệm cận đứng.
- Nếu thay \( x_i \) vào mà tử xuất hiện MATH ERROR thì loại \( x=x_i \).
- Trường hợp 2: Có một nghiệm \( x_i \) nào đó làm cho tử bằng 0.
- Nhân lượng liên hợp cho phân thức hoặc áp dụng \( a-b = \frac{a^2-b^2}{a+b} \); \( a+b = \frac{a^2-b^2}{a-b} \).
- Đưa thừa số vào căn theo công thức \( a\sqrt{b} = \begin{cases} \sqrt{a^2b} & \text{khi } a \ge 0 \\ -\sqrt{a^2b} & \text{khi } a < 0 \end{cases} \).
- Kiểm tra lại phân thức sau khi rút gọn xem nghiệm nào trong số \( x_i \) đã bị loại, các nghiệm còn lại của \( x_i \) là các đường tiệm cận đứng của đồ thị.
Ví dụ 6: Tìm tiệm cận
Tiệm cậnTìm tất cả các đường tiệm cận của đồ thị hàm số \( y=\frac{x+3}{\sqrt{x^2+1}} \).
A. \( x=1 \). B. \( y=\pm 1 \). C. \( y=1 \). D. \( y=-1 \).
Lời giải:
Cách giải 1: Phương pháp tự luận.
Vì tập xác định của hàm số là \( \mathbb{R} \) nên đồ thị hàm số không có tiệm cận đứng.
Ta có: \( \lim_{x \to +\infty} \frac{x+3}{\sqrt{x^2+1}} = \lim_{x \to +\infty} \frac{x(1+\frac{3}{x})}{|x|\sqrt{1+\frac{1}{x^2}}} = \lim_{x \to +\infty} \frac{1+\frac{3}{x}}{\sqrt{1+\frac{1}{x^2}}} = 1 \);
\( \lim_{x \to -\infty} \frac{x+3}{\sqrt{x^2+1}} = \lim_{x \to -\infty} \frac{x(1+\frac{3}{x})}{|x|\sqrt{1+\frac{1}{x^2}}} = \lim_{x \to -\infty} \frac{1+\frac{3}{x}}{-\sqrt{1+\frac{1}{x^2}}} = -1 \).
Vậy đồ thị hàm số có hai đường tiệm cận ngang là \( y=\pm 1 \).
Cách giải 2 (tham khảo thêm): Phương pháp trắc nghiệm.
Nhập vào máy tính bỏ túi như sau: \( \frac{X+3}{\sqrt{X^2+1}} \) CALC \( 10^{10} \) (nghĩa là thay x bởi một số vô cùng lớn).
Kết quả hiển thị là [1], tức là \( \lim_{x \to +\infty} y = 1 \).
Tương tự, nhập: \( \frac{X+3}{\sqrt{X^2+1}} \) CALC \( -10^{10} \) (nghĩa là thay x bởi một số vô cùng bé).
Kết quả hiển thị -0.9999999998. Số này gần bằng -1. Ta hiểu \( \lim_{x \to -\infty} y = -1 \).
Kết luận: Đáp án B.
Ví dụ 7: Tìm tiệm cận đứng
Tiệm cận đứngTìm tất cả các tiệm cận đứng của đồ thị hàm số \( y=\frac{2x-1-\sqrt{x^2+x+3}}{x^2-5x+6} \).
A. \( x=-3 \) và \( x=-2 \). B. \( x=-3 \). C. \( x=3 \) và \( x=2 \). D. \( x=3 \).
Lời giải:
Nhận xét: Nghiệm của mẫu là \( x=2, x=3 \); trong đó \( x=2 \) cùng là nghiệm của tử số (thay vào làm cho tử số bằng 0), vì vậy ta cần nhân lượng liên hợp trước khi tìm tiệm cận đứng của đồ thị.
Ta có: \( y = \frac{(2x-1)^2-(x^2+x+3)}{(x^2-5x+6)(2x-1+\sqrt{x^2+x+3})} = \frac{3x^2-5x-2}{(x-2)(x-3)(2x-1+\sqrt{x^2+x+3})} = \frac{(x-2)(3x+1)}{(x-2)(x-3)(2x-1+\sqrt{x^2+x+3})} = \frac{3x+1}{(x-3)(2x-1+\sqrt{x^2+x+3})} \).
Ta thấy trong hai nghiệm ban đầu \( x=2, x=3 \) thì nghiệm \( x=2 \) bị loại (đã bị rút gọn-không là tiệm cận đứng đồ thị), nên đồ thị chỉ còn tiệm cận đứng \( x=3 \).
Kết luận: Đáp án D.
Ví dụ 8: Tổng số tiệm cận
Tiệm cậnTổng số tiệm cận của đồ thị hàm số \( y=\frac{\sqrt{2x+1}-2}{x^2+x} \) là
A. 3. B. 0. C. 1. D. 2.
Lời giải:
Nhận xét: Trong hầu hết bài toán, ta nên tìm tiệm cận ngang của đồ thị trước tiệm cận đứng vì việc tìm tiệm cận ngang đơn giản hơn.
- Tìm tiệm cận ngang:
- Tìm tiệm cận đứng:
- Thay \( x=0 \) vào tử, ta có \( (\sqrt{2x+1}-2)|_{x=0} = -1 \ne 0 \) nên \( x=0 \) là tiệm cận đứng của đồ thị.
- Thay \( x=-1 \) vào tử, ta được MATH ERROR nên \( x=-1 \) không là tiệm cận đứng của đồ thị.
Bậc của tử là bậc của \( \sqrt{x} \), tức là bậc \( \frac{1}{2} \); bậc của mẫu là bậc 2. Vì bậc tử nhỏ hơn bậc mẫu và hàm số tồn tại giới hạn dương vô cực nên đồ thị luôn có tiệm cận ngang \( y=0 \).
Xét mẫu bằng 0 \( \Rightarrow x^2+x=0 \Rightarrow \begin{cases} x=0 \\ x=-1 \end{cases} \).
Nhận xét: Không có nghiệm nào trùng nghiệm tử (thay vào tử để biết) nên ta không nhân lượng liên hợp.
Kết luận: Đáp án D (2 tiệm cận).
Ví dụ 9: Số đường tiệm cận
Tiệm cậnĐồ thị hàm số \( y=\frac{5x+1-\sqrt{x+1}}{x^2-2x} \) có tất cả bao nhiêu đường tiệm cận?
A. 0. B. 1. C. 2. D. 3.
Lời giải:
Bậc tử là bậc 1 (bậc của 5x), bé hơn bậc mẫu (bậc 2) nên đồ thị hàm số có tiệm cận ngang \( y=0 \).
Vì nghiệm của mẫu là \( \{0;2\} \) trong đó \( x=0 \) cũng là nghiệm của tử nên ta cần nhân liên hợp cho hàm số. Ta được: \( y = \frac{(5x+1)^2-(x+1)}{(x^2-2x)(5x+1+\sqrt{x+1})} = \frac{25x^2+9x}{x(x-2)(5x+1+\sqrt{x+1})} = \frac{25x+9}{(x-2)(5x+1+\sqrt{x+1})} \).
Ta thấy chỉ còn \( x=2 \) thỏa mãn là tiệm cận đứng của đồ thị hàm số.
Kết luận: Đáp án C (2 tiệm cận).
Ví dụ 10: Số đường tiệm cận
Tiệm cậnTìm số đường tiệm cận của đồ thị hàm số \( y=\frac{x-1}{4\sqrt{3x+1}-3x-5} \).
A. 2. B. 3. C. 1. D. 0.
Lời giải:
Ta có: \( \lim_{x \to +\infty} \frac{x-1}{4\sqrt{3x+1}-3x-5} = \lim_{x \to +\infty} \frac{1-\frac{1}{x}}{4\sqrt{\frac{3}{x}+\frac{1}{x^2}}-3-\frac{5}{x}} = -\frac{1}{3} \); do đó \( y=-\frac{1}{3} \) là tiệm cận ngang của đồ thị hàm số.
Xét mẫu bằng 0 thì \( 4\sqrt{3x+1}=3x+5 \Rightarrow \begin{cases} 3x+5 \ge 0 \\ 16(3x+1)=9x^2+30x+25 \end{cases} \Rightarrow x=1 \) (trùng nghiệm tử).
Ta cần nhân liên hợp cho hàm số: \( y=\frac{(x-1)(4\sqrt{3x+1}+3x+5)}{16(3x+1)-(3x+5)^2} = \frac{(x-1)(4\sqrt{3x+1}+3x+5)}{-9x^2+18x-9} = \frac{4\sqrt{3x+1}+3x+5}{-9(x-1)} \).
Dễ thấy \( x=1 \) là tiệm cận đứng duy nhất của đồ thị hàm số. Vậy đồ thị hàm số có 2 đường tiệm cận.
Kết luận: Đáp án A.
TÌM TIỆM CẬN CỦA ĐỒ THỊ SỐ DỰA VÀO BẢNG BIẾN THIÊN
- Theo bảng biến thiên, nếu có \( \begin{cases} x \to \text{hằng số} \\ y \to \infty \end{cases} \) (*) thì đồ thị có tiệm cận đứng \( x=\text{hằng số} \).
- Theo bảng biến thiên, nếu có \( \begin{cases} x \to \infty \\ y \to \text{hằng số} \end{cases} \) thì đồ thị có tiệm cận ngang \( y=\text{hằng số} \).
(Lưu ý nếu giới hạn một bên tại \( x_0 \) thỏa (*) thì ta không cần xét giới hạn bên còn lại).
(Lưu ý khi tìm tiệm cận ngang của đồ thị, ta luôn xét đủ cả hai giới hạn khi x tiến về âm, dương vô cực).
Ví dụ 11: Tổng số tiệm cận
Tiệm cậnCho hàm số có bảng biến thiên như hình sau
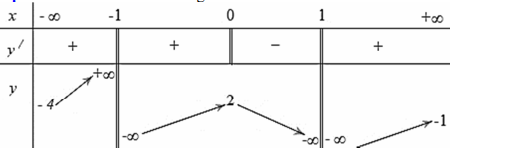
Tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số \( y=f(x) \) là
A. 3. B. 2. C. 4. D. 1.
Lời giải:
Ta có: \( \begin{cases} x \to -\infty \\ y \to -4 \end{cases} \) và \( \begin{cases} x \to +\infty \\ y \to -1 \end{cases} \) nên đồ thị có hai đường tiệm cận ngang \( y=-4; y=-1 \).
\( \begin{cases} x \to -1^+ \\ y \to +\infty \end{cases} \) nên đồ thị có tiệm cận đứng \( x=-1 \) (lúc này không cần xét giới hạn khi \( x \to -1^- \) nữa);
\( \begin{cases} x \to 1^- \\ y \to -\infty \end{cases} \) nên đồ thị có tiệm cận đứng \( x=1 \) (lúc này không cần xét giới hạn khi \( x \to 1^+ \) nữa). Do đó đồ thị hàm số có hai đường tiệm cận đứng \( x=1; x=-1 \).
Kết luận: Đáp án C (4 tiệm cận).
Ví dụ 12: Tổng số tiệm cận
Tiệm cậnCho hàm số \( y=f(x) \) có bảng biến thiên như sau
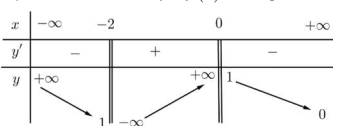
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho bằng
A. 2. B. 1. C. 0. D. 3.
Lời giải:
Ta có: \( \begin{cases} x \to -\infty \\ y \to +\infty \end{cases} \) (not) và \( \begin{cases} x \to +\infty \\ y \to 0 \end{cases} \) nên đồ thị có một đường tiệm cận ngang \( y=0 \).
Mặt khác: \( \begin{cases} x \to -2^+ \\ y \to -\infty \end{cases} \) và \( \begin{cases} x \to 0^- \\ y \to +\infty \end{cases} \) nên \( x=-2; x=0 \) là hai đường tiệm cận đứng của đồ thị.
Kết luận: Đáp án D (3 tiệm cận).
Ví dụ 13: Tổng số tiệm cận
Tiệm cậnCho hàm số \( y=f(x) \) xác định, liên tục trên \( \mathbb{R} \) và có bảng biến thiên như hình bên dưới:
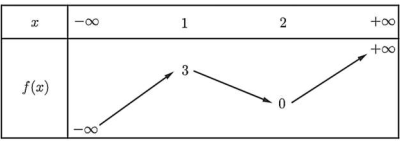
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số \( y=\frac{1}{2f(x)-1} \) là:
A. 4. B. 3. C. 1. D. 2.
Lời giải:
Khi \( x \to +\infty \) thì \( f(x) \to +\infty \); suy ra \( y=\frac{1}{2f(x)-1} \to 0 \) (do mẫu tiến về vô cùng), hay \( \lim_{x \to +\infty} y=0 \) nên đồ thị hàm số có tiệm cận ngang \( y=0 \).
Khi \( x \to -\infty \) thì \( f(x) \to -\infty \); suy ra \( y=\frac{1}{2f(x)-1} \to 0 \) (do mẫu tiến về vô cùng), hay \( \lim_{x \to -\infty} y=0 \) (đã kết luận).
Xét mẫu bằng 0 thì \( 2f(x)-1=0 \Rightarrow f(x)=\frac{1}{2} \Rightarrow x=a \lor x=b \lor x=c \) (a, b, c phân biệt).
Vậy đồ thị hàm số có ba đường tiệm cận đứng và một đường tiệm cận ngang.
Kết luận: Đáp án A (4 tiệm cận).
TIỆM CẬN CỦA ĐỒ THỊ HÀM CÓ CHỨA THAM SỐ
Ví dụ 14: Tìm tham số m
Tiệm cậnCho hàm số \( y=\frac{(m^2+m-3)x+m-3}{mx+1} \) biết đồ thị hàm số này có tiệm cận ngang đi qua điểm A(2025;-1). Tìm tất cả tham số m nguyên thỏa mãn điều kiện trên.
A. \( m=1 \). B. \( \begin{cases} m=2 \\ m=3 \end{cases} \). C. \( \begin{cases} m=1 \\ m=-3 \end{cases} \). D. \( m=2 \).
Lời giải:
Cần nhớ, điều kiện để đồ thị hàm số \( y=\frac{ax+b}{cx+d} \) có tiệm cận là \( \begin{cases} c \ne 0 \\ ad \ne bc \end{cases} \).
Áp dụng vào hàm số trên, ta có điều kiện: \( \begin{cases} m \ne 0 \\ m^2+m-3 \ne m(m-3) \end{cases} \Leftrightarrow \begin{cases} m \ne 0 \\ 4m \ne 3 \end{cases} \Leftrightarrow \begin{cases} m \ne 0 \\ m \ne \frac{3}{4} \end{cases} \).
Phương trình tiệm cận ngang của đồ thị: \( y=\frac{a}{c}=\frac{m^2+m-3}{m} \). Đường thẳng này đi qua A(2025,-1) nên \( \frac{m^2+m-3}{m}=-1 \Leftrightarrow m^2+2m-3=0 \Leftrightarrow \begin{cases} m=1 \\ m=-3 \end{cases} \).
Kết luận: Đáp án C.
Ví dụ 15: Tìm giá trị m
Tiệm cậnVới giá trị nào của m thì đồ thị (C): \( y=\frac{mx-1}{2x+m} \) có tiệm cận đứng qua điểm \( M(-1;\sqrt{2}) \)?
A. \( m=0 \). B. \( m=2 \). C. \( m=\frac{1}{2} \). D. \( m=\frac{\sqrt{2}}{2} \).
Lời giải:
Đ đồ thị hàm số đã cho có tiệm cận khi và chỉ khi \( \begin{cases} c=2 \ne 0 \\ ad-bc=m^2+2 > 0 \end{cases} \) (đúng \( \forall m \in \mathbb{R} \)).
Tiệm cận đứng của đồ thị: \( x = -\frac{m}{2} \). Đường thẳng này qua \( M(-1;\sqrt{2}) \) suy ra \( -\frac{m}{2}=-1 \Leftrightarrow m=2 \).
Kết luận: Đáp án B.
Ví dụ 16: Tìm giá trị m
Tiệm cậnTìm tất cả giá trị của m để đồ thị hàm số \( y=\frac{x-m}{mx-1} \) không có tiệm cận đứng.
A. \( m=1 \). B. \( m=-1 \). C. \( m=\pm 1 \). D. \( m=0; m=\pm 1 \).
Lời giải:
Xét \( m=0 \). Hàm số trở thành \( y=-x \) nên đồ thị không có đường tiệm cận đứng.
Xét \( m \ne 0 \). Khi đó đồ thị hàm số không có đường tiệm cận đứng \( \Leftrightarrow ad-bc=0 \Leftrightarrow -1+m^2=0 \Leftrightarrow m=\pm 1 \).
Vậy giá trị của m cần tìm là \( m=0; m=\pm 1 \).
Kết luận: Đáp án D.
Ví dụ 17: Tìm giá trị m
Tiệm cậnCho hàm số \( y=\frac{x-1}{x^2-mx-2} \). Giá trị của m để đồ thị hàm số có 2 đường tiệm cận đứng là:
A. \( m \ne -1 \). B. \( m=-1 \). C. \( m \in \mathbb{R} \). D. \( m \ne 1 \).
Lời giải:
Để đồ thị hàm số \( y=\frac{x-1}{x^2-mx-2} \) có 2 đường tiệm cận đứng thì \( g(x)=x^2-mx-2=0 \) có hai nghiệm phân biệt khác 1 \( \Leftrightarrow \begin{cases} \Delta_g=m^2+8 > 0 \\ g(1)=1-m-2 \ne 0 \end{cases} \Leftrightarrow m \ne -1 \).
Kết luận: Đáp án A.
Ví dụ 18: Tìm giá trị m
Tiệm cậnCho hàm số \( y=\frac{mx-1}{x^2-3x} \) (1). Tìm tất cả giá trị của m để đồ thị hàm số (1) có hai tiệm cận đứng.
A. \( m \in \mathbb{R} \). B. \( m \ne 3 \). C. \( m \ne \frac{1}{3} \). D. \( m=3 \).
Lời giải:
Xét mẫu bằng 0 thì \( x^2-3x=0 \Rightarrow x=0 \lor x=3 \).
Để đồ thị hàm số \( y=\frac{mx-1}{x^2-3x} \) có hai đường tiệm cận đứng thì phương trình: \( mx-1=0 \) không nhận \( x=0 \) và \( x=3 \) là nghiệm \( \Leftrightarrow \begin{cases} m.0-1 \ne 0 \\ m.3-1 \ne 0 \end{cases} \Leftrightarrow m \ne \frac{1}{3} \).
Kết luận: Đáp án C.
Ví dụ 19: Số giá trị m
Tiệm cậnCho hàm số \( y=\frac{x-2}{mx^2-2x+4} \). Có tất cả bao nhiêu giá trị của tham số m để đồ thị hàm số có đúng hai đường tiệm cận (tiệm cận đứng và tiệm cận ngang)?
A. 0. B. 2. C. 3. D. 1.
Lời giải:
Với \( m=0 \) thì hàm số trở thành \( y=\frac{x-2}{-2x+4}=-\frac{1}{2} \) (không thỏa mãn).
Với \( m \ne 0 \) thì \( \lim_{x \to \pm\infty} \frac{x-2}{mx^2-2x+4} = 0 \Rightarrow y=0 \) là tiệm cận ngang của đồ thị hàm số.
Do đó ta cần tìm m để đồ thị hàm số có đúng một tiệm cận đứng. Khi đó \( mx^2-2x+4=0 \) có nghiệm duy nhất hoặc \( mx^2-2x+4=0 \) có hai nghiệm phân biệt trong đó có một nghiệm \( x=2 \).
- \( mx^2-2x+4=0 \) có nghiệm duy nhất \( \Leftrightarrow \Delta'=0 \Leftrightarrow 1-4m=0 \Leftrightarrow m=\frac{1}{4} \).
- \( mx^2-2x+4=0 \) có hai nghiệm phân biệt trong đó có một nghiệm \( x=2 \).
\( \begin{cases} \Delta' > 0 \\ m.2^2-2.2+4=0 \end{cases} \Leftrightarrow \begin{cases} m < \frac{1}{4} \\ m=0 \end{cases} \Rightarrow m=0 \). Vậy có hai giá trị của m thỏa mãn đề bài.
Kết luận: Đáp án B.
Ví dụ 20: Tìm tham số m
Tiệm cậnTìm tất cả tham số m để đồ thị hàm số \( y=\frac{x+1}{\sqrt{mx^2+1}} \) có hai tiệm cận ngang.
A. Không có m thỏa mãn. B. \( m < 0 \). C. \( m=0 \). D. \( m>0 \).
Lời giải:
Điều kiện xác định: \( mx^2+1 \ge 0 \). (*)
Nếu \( m=0 \) thì hàm số trở thành \( y=x+1 \), đồ thị hàm này không có tiệm cận ngang.
Nếu \( m<0 \) thì
Nếu \( m<0 \) thì \( \lim_{x \to \pm\infty} y \) không tồn tại (do điều kiện (*) không được thỏa mãn). Nếu \( m>0 \) thì: \( \lim_{x \to +\infty} y = \lim_{x \to +\infty} \frac{x(1+\frac{1}{x})}{x\sqrt{m+\frac{1}{x^2}}} = \frac{1}{\sqrt{m}} \); \( \lim_{x \to -\infty} y = \lim_{x \to -\infty} \frac{x(1+\frac{1}{x})}{-x\sqrt{m+\frac{1}{x^2}}} = -\frac{1}{\sqrt{m}} \). Điều này đồng nghĩa việc đồ thị hàm số có hai đường tiệm cận ngang là \( y=\pm\frac{1}{\sqrt{m}} \). Kết luận: Đáp án D.
TIỆM CẬN ĐỒ THỊ VÀ CÁC YẾU TỐ HÌNH HỌC
Ví dụ 21: Tính khoảng cách và diện tích
Tiệm cậnCho hàm số \( y=\frac{2x^2-x}{x-1} \) có đồ thị (C).
a) Tính khoảng cách từ M(2;1) đến đường tiệm cận đứng của đồ thị hàm số (C).
b) Đường tiệm cận xiên của đồ thị hàm số (C) cắt hai trục tọa độ lần lượt tại hai điểm A, B. Tính diện tích của tam giác OAB đó.
Lời giải:
a) Đồ thị (C) có đường tiệm cận đứng: \( d_1: x-1=0 \).
Ta có: \( d(M, d_1) = \frac{|2-1|}{\sqrt{1^2}} = 1 \).
b) Ta có \( y = \frac{2x^2-x}{x-1} = 2x+1+\frac{1}{x-1} \) và \( \lim_{x \to \pm\infty} [y-(2x+1)] = \lim_{x \to \pm\infty} \frac{1}{x-1} = 0 \) nên đồ thị hàm số (C) có tiệm cận xiên là \( y=2x+1 \) (\( d_2 \)).
Tiệm cận xiên cắt Ox tại \( A(-\frac{1}{2};0) \), cắt trục Oy tại \( B(0;1) \) nên \( S_{OAB} = \frac{1}{2}OA.OB = \frac{1}{2}|-\frac{1}{2}|.|1|=\frac{1}{4} \).
Ví dụ 22: Số điểm thỏa mãn
Tiệm cậnCho hàm số \( y=\frac{2x+2}{2x-3} \) có đồ thị (C). Có bao nhiêu điểm M thuộc (C) sao cho khoảng cách từ điểm M đến đường tiệm cận ngang bằng 10 lần khoảng cách từ điểm M đến đường tiệm cận đứng.
A. 1. B. 2. C. 3. D. 4.
Lời giải:
Ta có các đường thẳng \( x=\frac{3}{2} \) và \( y=1 \) lần lượt là đường tiệm cận đứng và đường tiệm cận ngang của đồ thị hàm số.
Gọi \( M(x; \frac{2x+2}{2x-3}) \in (C) \) với \( x \ne \frac{3}{2} \).
Khoảng cách từ điểm M đến đường tiệm cận đứng bằng \( |x-\frac{3}{2}|=\frac{|2x-3|}{2} \).
Khoảng cách từ điểm M đến đường tiệm cận ngang bằng \( |\frac{2x+2}{2x-3}-1|=\frac{5}{|2x-3|} \).
Khi đó: \( \frac{5}{|2x-3|}=10.\frac{|2x-3|}{2} \Leftrightarrow (2x-3)^2=1 \Leftrightarrow 4x^2-12x+8=0 \Leftrightarrow \begin{cases} x=2 \Rightarrow M(2;6) \\ x=1 \Rightarrow M(1;-4) \end{cases} \).
Kết luận: Đáp án B (2 điểm).
Ví dụ 23: Tìm giá trị a
Tiệm cậnCho đồ thị hai hàm số \( f(x)=\frac{x+1}{x-1} \) và \( g(x)=\frac{ax+1}{x-2}, a \ne -\frac{1}{2} \). Tìm tất cả các giá trị thực dương của a để các tiệm cận của hai đồ thị hàm số tạo thành một hình chữ nhật có diện tích là 4.
A. \( a=2 \). B. \( a=4 \). C. \( a=3 \). D. \( a=5 \).
Lời giải:
Đồ thị hàm số \( f(x)=\frac{x+1}{x-1} \) có hai đường tiệm cận là \( x=1 \) và \( y=1 \).
Đồ thị hàm số \( g(x)=\frac{ax+1}{x-2} \) có hai đường tiệm cận là \( x=2 \) và \( y=a \).
Hình chữ nhật được tạo thành từ bốn đường tiệm cận của hai đồ thị trên có hai kích thước lần lượt là 1 và \( |a-1| \). Theo giả thiết: \( |a-1|.1=4 \Leftrightarrow \begin{cases} a=5 \\ a=-3 \end{cases} \). Vì \( a>0 \) nên chọn \( a=5 \).
Kết luận: Đáp án D.
Ví dụ 24: Tìm tổng a+2b
Tiệm cậnCho hàm số \( y=\frac{2x-1}{x-1} \) có đồ thị (C). Gọi M(a;b) là điểm thuộc đồ thị hàm số có hoành độ dương sao cho tổng khoảng cách từ M đến hai tiệm cận của (C) nhỏ nhất. Khi đó tổng a+2b bằng
A. 8. B. 5. C. 2. D. 7.
Lời giải:
Hàm số \( y=\frac{2x-1}{x-1} \) có đường tiệm cận ngang \( d_1: y=2 \) và đường tiệm cận đứng \( d_2: x=1 \). Khi đó:
\( d(M,d_1)=|b-2|=|\frac{2a-1}{a-1}-2|=\frac{1}{|a-1|} \); \( d(M,d_2)=|a-1| \).
Khi đó \( d(M,d_1)+d(M,d_2)=|a-1|+\frac{1}{|a-1|} \ge 2\sqrt{|a-1|.\frac{1}{|a-1|}}=2 \) (bất đẳng thức Cau-chy).
Vậy tổng khoảng cách nhỏ nhất là 2 khi \( |a-1|=\frac{1}{|a-1|} \Leftrightarrow (a-1)^2=1 \Leftrightarrow a^2-2a=0 \Leftrightarrow \begin{cases} a=0 \\ a=2 \end{cases} \).
So điều kiện ta thấy \( a=2 \) thỏa mãn. Suy ra \( b=\frac{2.2-1}{2-1}=3 \Rightarrow a+2b=8 \).
Kết luận: Đáp án A.
BÀI TOÁN THỰC TẾ VỀ TIỆM CẬN ĐỒ THỊ HÀM SỐ
Ví dụ 25: Ứng dụng thực tế
Tiệm cậnSố lượng sản phẩm X bán được của một công ty trong x tháng được cho bởi công thức \( T(x) = 150(6 - \frac{5}{x+2}) \) trong đó \( x \ge 1 \).
a) Tìm tiệm cận ngang của đồ thị hàm số trên.
b) Nếu x đủ lớn thì số lượng sản phẩm X bán được của công ty trong x tháng là bao nhiêu?
Lời giải:
a) Ta có: \( \lim_{x \to +\infty} T(x) = 150 \lim_{x \to +\infty} (6-\frac{5}{x+2}) = 150 \cdot 6 = 900 \). Vậy đường thẳng \( y=900 \) là tiệm cận ngang của đồ thị hàm số.
b) Nếu số tháng sản xuất (x) là đủ lớn thì số lượng sản phẩm X bán ra trong x tháng của công ty là 900 sản phẩm.
Ví dụ 26: Ứng dụng trong vật lý
Tiệm cậnTrong thuyết tương đối của Einstein, khối lượng của vật chuyển động với vận tốc v được cho bởi công thức \( m(v) = \frac{m_0}{\sqrt{1-\frac{v^2}{c^2}}} \), trong đó \( m_0 \) là khối lượng của vật khi đứng yên, c là vận tốc ánh sáng, m(v) là hàm theo biến v.
a) Tìm đường tiệm cận của đồ thị hàm số đã cho.
b) Khi vận tốc của vật càng gần với vận tốc ánh sáng thì khối lượng của vật thay đổi thế nào?
Lời giải:
a) Ta có: \( \lim_{v \to c^-} m(v) = \lim_{v \to c^-} \frac{m_0}{\sqrt{1-\frac{v^2}{c^2}}} = +\infty \) (vì \( \sqrt{1-\frac{v^2}{c^2}} \to 0 \) và \( 1-\frac{v^2}{c^2}>0 \) khi \( v
Do vậy đường thẳng \( v=c \) là một tiệm cận đứng của đồ thị hàm số \( y=m(v) \).
b) Ta thấy khối lượng của vật sẽ vô cùng lớn (dần về vô cực) khi vận tốc của vật tiến dần về vận tốc ánh sáng.
Ví dụ 27: Ứng dụng thực tế
Tiệm cậnĐể loại bỏ x% chất gây ô nhiễm không khí từ khí thải của một nhà máy, người ta ước tính chi phí cần bỏ ra là \( C(x) = \frac{300x}{100-x} \) (triệu đồng), \( 0 \le x < 100 \).
Hãy cho biết:
a) Chi phí cần bỏ ra sẽ thay đổi như thế nào khi x tăng?
b) Có thể loại bỏ được 100% chất gây ô nhiễm không khí không? Vì sao?
Lời giải:
Tập xác định: \( D=[0;100) \).
Xét hàm số \( y=C(x)=\frac{300x}{100-x}, 0 \le x < 100 \). Ta có: \( y' = \frac{30000}{(100-x)^2} > 0 \), với mọi \( x \in [0;100) \).
Do đó hàm số luôn đồng biến trên nửa khoảng \( [0;100) \).
\( \lim_{x \to 100^-} C(x) = \lim_{x \to 100^-} \frac{300x}{100-x} = +\infty \), nên đồ thị hàm số có tiệm cận đứng là \( x=100 \).
a) Chi phí cần bỏ ra \( C(x) \) sẽ luôn tăng khi x tăng.
b) Vì \( \lim_{x \to 100^-} C(x) = +\infty \) (hàm số \( C(x) \) không xác định khi \( x=100 \)).
Nên nhà máy không thể loại bỏ 100% chất gây ô nhiễm không khí (dù bỏ ra chi phí là bao nhiêu đi chăng nữa).
Ví dụ 28: Ứng dụng thực tế
Tiệm cậnSố lượng sản phẩm bán được của một công ty trong x (tháng) được tính theo công thức \( S(x) = 200(5-\frac{9}{2+x}) \), trong đó \( x \ge 1 \).
a) Xem \( y=S(x) \) là một hàm số xác định trên nửa khoảng \( [1;+\infty) \), hãy tìm tiệm cận ngang của đồ thị hàm số đó.
b) Nêu nhận xét về số lượng sản phẩm bán được của công ty đó trong x (tháng) khi x đủ lớn.
Lời giải:
a) Ta có \( \lim_{x \to +\infty} y = \lim_{x \to +\infty} 200(5-\frac{9}{2+x}) = 1000 \).
Vậy đường thẳng \( y=1000 \) là tiệm cận ngang của đồ thị hàm số đã cho.
b) Khi x đủ lớn thì số lượng sản phẩm bán được của công ty sẽ tiến gần đến 1000.
Ví dụ 29: Ứng dụng thực tế
Tiệm cậnMột bể chứa 5000 lít nước tinh khiết. Người ta bơm vào bể đó nước muối có nồng độ 30 gam muối cho mỗi lít nước với tốc độ 25 lít/phút.
a) Chứng tỏ nồng độ muối trong bể sau t phút (tính bằng tỉ số của khối lượng muối trong bể và thể tích nước trong bể, đơn vị: gam/lít) là \( f(t) = \frac{30t}{200+t} \).
b) Xem \( y=f(t) \) là một hàm số xác định trên nửa khoảng \( [0;+\infty) \), hãy tìm tiệm cận ngang của đồ thị hàm số đó.
c) Nêu nhận xét về nồng độ muối trong bể sau thời gian t ngày càng lớn.
Lời giải:
a) Sau t phút, ta có khối lượng muối trong bể là \( 25 \cdot 30t = 750t \) (gam).
Thể tích của lượng nước trong bể là \( 5000+25t \) (lít).
Vậy nồng độ muối sau t phút là \( f(t) = \frac{750t}{5000+25t} = \frac{30t}{200+t} \) (gam/lít).
b) Ta có: \( \lim_{t \to +\infty} f(t) = \lim_{t \to +\infty} \frac{30t}{200+t} = \lim_{t \to +\infty} \frac{30}{\frac{200}{t}+1} = 30 \).
Vậy đường thẳng \( y=30 \) là tiệm cận ngang của đồ thị hàm số \( f(t) \).
c) Ta có đồ thị hàm số \( y=f(t) \) nhận đường thẳng \( y=30 \) làm tiệm cận ngang, tức là khi t càng lớn thì nồng độ muối trong bể sẽ tiến gần đến mức 30 (gam/lít). Lúc đó, nồng độ muối trong bể sẽ gần như bằng nồng độ muối trong nước muối được bơm vào bể.
Ví dụ 30: Tiệm cận xiên
Tiệm cậnMột ống khói của nhà máy điện hạt nhân có mặt cắt là một hypebol (H) có phương trình chính tắc là \( \frac{x^2}{27^2}-\frac{y^2}{40^2}=1 \). Xét hai nhánh bên trên Ox của (H) là đồ thị (C) của hàm số \( y=\frac{40}{27}\sqrt{x^2-27^2} \) (phần nét liền đậm). Chứng minh rằng đường thẳng \( y=\frac{40}{27}x \) là một đường tiệm cận xiên của (C). Hãy chỉ ra thêm một đường tiệm cận xiên khác của (C).
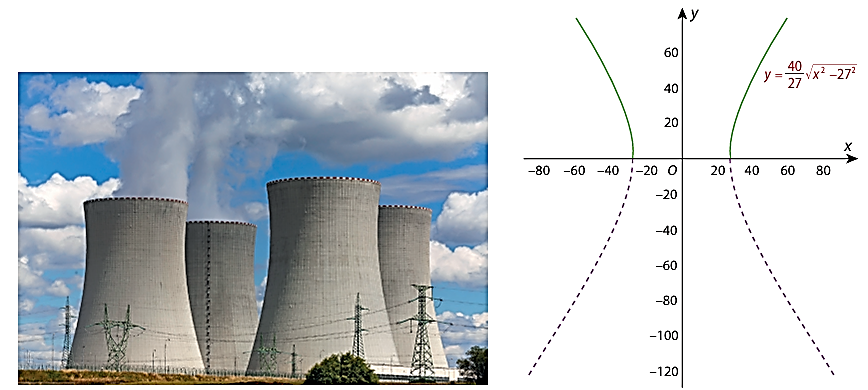
Lời giải:
Xét \( \lim_{x \to +\infty} (\frac{40}{27}\sqrt{x^2-27^2} - \frac{40}{27}x) = \lim_{x \to +\infty} \frac{40}{27} \frac{(x^2-27^2)-x^2}{\sqrt{x^2-27^2}+x} = \lim_{x \to +\infty} \frac{40}{27} \frac{-27^2}{\sqrt{x^2-27^2}+x} = 0 \).
Vậy đường thẳng \( y=\frac{40}{27}x \) là một đường tiệm cận xiên của (C).
Xét nhánh còn lại, ta có \( \lim_{x \to -\infty} (\frac{40}{27}\sqrt{x^2-27^2} - (-\frac{40}{27}x)) = \lim_{x \to -\infty} \frac{40}{27} (\sqrt{x^2-27^2} + x) = \lim_{x \to -\infty} \frac{40}{27} \frac{x^2-27^2-x^2}{\sqrt{x^2-27^2}-x} = \lim_{x \to -\infty} \frac{40}{27} \frac{-27^2}{\sqrt{x^2-27^2}-x} = 0 \).
Vậy đường thẳng \( y=-\frac{40}{27}x \) là một đường tiệm cận xiên khác của (C).
Ví dụ 31: Ứng dụng thực tế
Tiệm cậnTại một công ty sản xuất đồ chơi A, công ty phải chi 50000 USD để thiết lập dây chuyền sản xuất ban đầu. Sau đó, cứ sản xuất được một sản phẩm đồ chơi A, công ty phải trả 5 USD cho nguyên liệu thô và nhân công. Gọi x (\( x \ge 1 \)) là số đồ chơi A mà công ty đã sản xuất và T(x) (đơn vị USD) là tổng số tiền bao gồm cả chi phí ban đầu mà công ty phải chi trả khi sản xuất x đồ chơi A. Người ta xác định chi phí trung bình cho mỗi sản phẩm đồ chơi A là \( M(x) = \frac{T(x)}{x} \).

a) Xem M(x) là hàm số theo x xác định trên nửa khoảng \( [1;+\infty) \), tìm tiệm cận ngang của đồ thị hàm số này.
b) Nêu nhận xét về chi phí trung bình cho mỗi sản phẩm đồ chơi A khi x đủ lớn.
Lời giải:
a) Tổng chi phí: \( T(x)=50000+5x \). Chi phí trung bình: \( M(x)=\frac{50000}{x}+5 \).
Khi \( x \to +\infty \), \( \frac{50000}{x} \to 0 \) nên \( M(x) \to 5 \). Tiệm cận ngang: \( y=5 \).
b) Nhận xét khi x đủ lớn: Chi phí trung bình \( M(x) \) tiến gần đến 5 USD, là chi phí biến đổi mỗi sản phẩm. Chi phí cố định ban đầu không ảnh hưởng đáng kể khi sản xuất quy mô lớn.
Ví dụ 32: Tiệm cận xiên và ứng dụng
Tiệm cậnTrong hình bên, đường viền bóng của đèn ngủ lên tường là đồ thị của hàm số \( y=55-\frac{1}{2}\sqrt{x^2+144} \) với x và y tính bằng đơn vị centimet.
a) Chứng minh rằng \( y=55-\frac{1}{2}x \) là một tiệm cận xiên của đồ thị hàm số này.
b) Nếu trong một ngày, một xưởng sản xuất được x kilôgam sản phẩm thì chi phí trung bình (tính bằng nghìn đồng) cho một sản phẩm được cho bởi công thức: \( C(x)=\frac{50x+2000}{x} \). Tìm các đường tiệm cận của hàm số \( C(x) \).

Lời giải:
a) Để chứng minh \( y=55-\frac{1}{2}x \) là tiệm cận xiên, ta xét \( \lim_{x \to +\infty} [(55-\frac{1}{2}\sqrt{x^2+144}) - (55-\frac{1}{2}x)] = \lim_{x \to +\infty} \frac{1}{2}(x-\sqrt{x^2+144}) = \lim_{x \to +\infty} \frac{1}{2}\frac{x^2-(x^2+144)}{x+\sqrt{x^2+144}} = \lim_{x \to +\infty} \frac{-72}{x+\sqrt{x^2+144}}=0 \).
Vậy \( y=55-\frac{1}{2}x \) là đường tiệm cận xiên của đồ thị hàm số \( y=55-\frac{1}{2}\sqrt{x^2+144} \).
b) Tìm các đường tiệm cận của đồ thị hàm chi phí trung bình \( C(x) \).
- \( \lim_{x \to +\infty} C(x) = \lim_{x \to +\infty} (50+\frac{2000}{x}) = 50 \). Vậy \( y=50 \) là tiệm cận ngang của \( C(x) \).
- \( \lim_{x \to 0^+} C(x) = \lim_{x \to 0^+} (50+\frac{2000}{x}) = +\infty \). Vậy \( x=0 \) (trục Oy) là tiệm cận đứng của \( C(x) \).
- Đồ thị hàm số \( C(x) \) có tiệm cận ngang nên không có tiệm cận xiên.
Ví dụ 33: Ứng dụng thực tế
Tiệm cậnNồng độ oxygen trong hồ theo thời gian t cho bởi công thức \( y(t)=5-\frac{15t}{9t^2+1} \) với y được tính theo mg/l và t được tính theo giờ, \( t \ge 0 \). Tìm các đường tiệm cận của đồ thị hàm số \( y(t) \). Từ đó, có nhận xét gì về nồng độ oxygen trong hồ khi thời gian t trở nên rất lớn?

Lời giải:
- Ta có \( \lim_{t \to +\infty} y(t) = 5 \) \( \Rightarrow y=5 \) là tiệm cận ngang của đồ thị hàm số.
- Đồ thị không có tiệm cận đứng vì mẫu số \( 9t^2+1 \ne 0, \forall t \ge 0 \).
Nhận xét: Khi t rất lớn, nồng độ oxygen tiến đến 5mg/l và ổn định.
