LỚP TOÁN THẦY BÌNH

Question 1. Cho hàm số $f(x) = \frac{x^2-3x-4}{x^2-16}$.

a) Tập xác định của hàm số $f(x)$ là $D = \mathbb{R} \setminus \{\pm 4\}$ True False

b) $x = \pm 4$ là hai tiệm cận đứng của đồ thị hàm số đã cho True False

c) $y = -1$ là tiệm cận ngang của đồ thị hàm số đã cho True False

d) Đồ thị hàm số đã cho không có tiệm cận xiên True False

Question 2. Cho hàm số $y=f(x)$ xác định trên $\mathbb{R}\setminus\{-2\}$, liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình dưới đây.

a) Đồ thị hàm số không có tiệm cận ngang True False

b) Tiệm cận đứng của đồ thị hàm số có phương trình: $x = -2$ True False

c) Đồ thị hàm số có hai đường tiệm cận ngang có phương trình: $x=3$ và $x=4$ True False

d) Đồ thị hàm số có ba đường tiệm cận True False

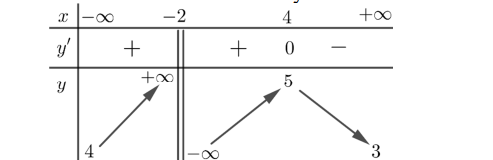
Question 3. Cho hàm số $y = \frac{\sqrt{4x^2-9}}{x-1}$. Khi đó:

a) Đường thẳng $y=2$ là tiệm cận ngang của đồ thị hàm số True False

b) Đồ thị hàm số có tiệm cận đứng là $x=1$ True False

c) Đường thẳng $y=-2$ là tiệm cận ngang của đồ thị hàm số True False

d) Đồ thị hàm số có đúng hai đường tiệm cận True False

Question 4. Cho hàm số $y = f(x)$ có bảng biến thiên như hình vẽ.

a) Hàm số đã cho có hai điểm cực trị True False

b) $\max_{(- \infty; 2)} f(x) = 5$ True False

c) Đồ thị hàm số đã cho có duy nhất một đường tiệm cận ngang True False

d) Đường thẳng $x=-2$ là tiệm cận đứng của đồ thị hàm số True False

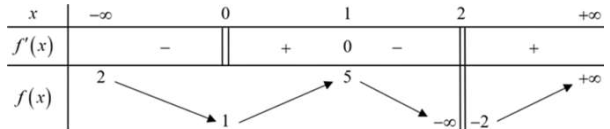
Question 5. Giả sử số dân của một thị trấn sau $t$ năm kể từ năm 2000 được mô tả bởi hàm số $N(t) = \frac{25t+10}{t+5}$, $t \ge 0$. Trong đó $N(t)$ được tính bằng nghìn người. Khi đó:

a) Dân số của thị trấn đó năm 2000 là 2000 người True False

b) Dân số của thị trấn đó năm 2015 là 19200 người True False

c) Hàm số $N'(t) = \frac{115}{(t+5)^2}$ True False

d) Dân số của thị trấn đó luôn tăng nhưng không vượt quá 25000 người True False

Question 6. Nồng độ oxygen trong hồ theo thời gian $t$ cho bởi công thức $y(t) = 5 - \frac{15t}{9t^2+1}$, với $y$ được tính theo mg/l và $t$ được tính theo giờ, $t \ge 0$.

a) Đồ thị hàm số $y(t)$ có một đường tiệm cận ngang và một đường tiệm cận xiên True False

b) Đồ thị hàm số có đường tiệm cận ngang là $y=5$ True False

c) Đồ thị hàm số có đường tiệm cận đứng là $x = \frac{1}{3}$ True False

d) Sau một thời gian đủ dài, nồng độ oxygen trong hồ sẽ bão hòa và đạt ngưỡng 5 mg/l True False

Question 7. Cho hàm số $y = \frac{x^2-2x+2}{x+2}$. Khi đó:

a) Hàm số có hai tiệm cận True False

b) Giao điểm của hai tiệm cận là $I(-2;-6)$ True False

c) Khoảng cách từ O đến tiệm cận xiên bằng $4\sqrt{2}$ True False

d) Tiệm cận xiên của hàm số đi qua điểm $M(0;-4)$ True False

Question 8. Để loại bỏ $x\%$ chất gây ô nhiễm không khí từ khí thải của một nhà máy, người ta ước tính chi phí cần loại bỏ là: $C(x) = \frac{300x}{100-x}$ (triệu đồng), $0 \le x < 100$. Khi đó:

a) $C'(x) = \frac{30000}{(100-x)^2}$ với mọi $x \in [0;100)$ True False

b) Để loại bỏ được 50\% chất gây ô nhiễm cần 300 triệu đồng True False

c) Chi phí bỏ ra luôn tăng khi $x$ tăng True False

d) Không thể loại bỏ 100\% chất gây ô nhiễm dù bỏ ra chi phí là bao nhiêu đi chăng nữa True False

Question 9. Giả sử một loại virus truyền nhiễm gây bệnh cho người. Số người bị nhiễm sau $t$ ngày được cho bởi công thức $N(t) = \frac{8000}{5+C \cdot e^{-t}}$. Ban đầu người ta phát hiện có 4 người nhiễm bệnh. Khi đó:

a) $C = 1995$ True False

b) Sau 3 ngày sẽ có khoảng 77 người nhiễm bệnh (làm tròn đến hàng đơn vị) True False

c) Kể từ ngày thứ 40 trở đi thì số lượng người nhiễm bệnh sẽ giảm dần True False

d) Số người nhiễm bệnh luôn tăng nhưng không vượt qua 1600 người True False

Question 10. Giả sử số lượng của một quần thể nấm men tại môi trường nuôi cấy trong phòng thí nghiệm được mô hình hóa bằng hàm số $P(t) = \frac{a}{b+e^{-0,75t}}$, trong đó thời gian $t$ được tính bằng giờ. Tại thời điểm ban đầu $t=0$, quần thể có 20 tế bào và tăng với tốc độ 12 tế bào/giờ. Khi đó:

a) $a=25$ True False

b) $b=\frac{1}{2}$ True False

c) Số lượng quần thể nấm men luôn tăng True False

d) Số lượng quần thể nấm men luôn tăng nhưng không vượt quá 50 tế bào True False

Question 11. Cho hàm số $y = \frac{x^2+mx-1}{x-1}$ ($C_m$) ($m$ là tham số). Các mệnh đề sau đúng hay sai?

a) Đồ thị hàm số ($C_m$) có tiệm cận xiên khi và chỉ khi $m \neq 0$ True False

b) Để tiệm cận xiên của ($C_m$) đi qua $M(2;-5)$ thì $m=-8$ True False

c) Để tiệm cận xiên của ($C_m$) tạo với hai trục toạ độ một tam giác có diện tích bằng 8 thì tổng tất cả các giá trị $m$ tìm được bằng 2 True False

d) Với $m=3$ thì giao điểm của hai đường tiệm cận của ($C_m$) nằm trên Parabol $y = x^2+3$ True False

Question 12. Cho hàm số $y = f(x)$ xác định trên $\mathbb{R} \setminus \{-1; 1\}$ liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:

a) Đồ thị hàm số $y = f(x)$ có đường tiệm cận đứng $x=1$ True False

b) Đồ thị hàm số $y = f(x)$ có đúng hai đường tiệm cận ngang True False

c) Đồ thị hàm số $y = f(x)$ không có đường tiệm cận xiên True False

d) Đồ thị hàm số $y = \frac{1}{f(x)+1}$ có tất cả bốn đường tiệm cận True False

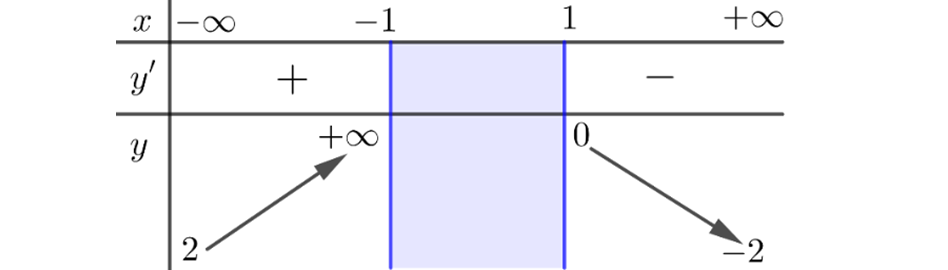
Question 13. Cho hàm số $y = f(x) = x+2+\frac{3}{2x+1}$ có đồ thị là (C).

a) (C) có đường tiệm cận đứng là $x=-\frac{1}{2}$ True False

b) $\lim_{x \to +\infty} [f(x)-(x+2)]=0$ True False

c) (C) có đường tiệm cận xiên là $y=2x+1$ True False

d) (C) có tâm đối xứng $(-\frac{1}{2}; 2)$ True False

Question 14. Cho hàm số $y = \frac{ax+1}{bx-2}$ (1) với $a, b$ là các tham số.

a) Với $a=1, b=2$ thì đồ thị hàm số (1) có hai đường tiệm cận True False

b) Điều kiện để đồ thị hàm số (1) có tiệm cận là $2a+b \neq 0$ True False

c) Khi đồ thị hàm số (1) có tiệm cận thì tiệm cận đứng của nó là $y=\frac{a}{b}$ và tiệm cận ngang của nó là $x=\frac{2}{b}$ True False

d) Nếu đồ thị hàm số (1) có tiệm cận đứng $x=2$ và tiệm cận ngang $y=3$ thì $a-2b=1$ True False

Question 15. Cho hàm số $y = \frac{(m+1)x^2+(2m+1)x+m+2}{x+1}$.

a) Với mọi số thực $m$ thì tiệm cận đứng của đồ thị hàm số là $x=-1$ True False

b) Tiệm cận xiên của đồ thị hàm số đi qua điểm $M(1;2)$ khi $m=\frac{1}{2}$ True False

c) Khi $m=1$ thì tiệm cận xiên của đồ thị hàm số vuông góc với đường thẳng $d: 3x+4y-5=0$ True False

d) Với $m \neq -1$ thì tâm đối xứng của đồ thị hàm số luôn thuộc Parabol $(P): y = -x^2$ True False

Question 16. Cho hàm số $y=f(x)$ xác định trên $\mathbb{R}\setminus\{-2\}$, liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình dưới đây.

a) Đồ thị hàm số không có tiệm cận ngang True False

b) Tiệm cận đứng của đồ thị hàm số có phương trình: $x=-2$ True False

c) Đồ thị hàm số có hai đường tiệm cận ngang có phương trình: $x=3$ và $x=4$ True False

d) Đồ thị hàm số có ba đường tiệm cận True False

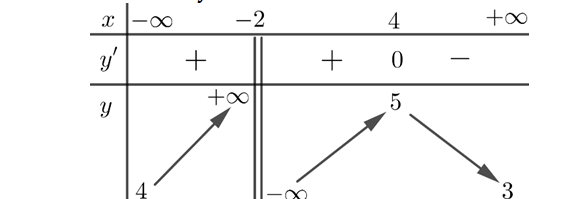
Question 17. Cho hàm số $y=\frac{\sqrt{4x^2-9}}{x-1}$.

a) Đường thẳng $y=2$ là tiệm cận ngang của đồ thị hàm số True False

b) Đồ thị hàm số có tiệm cận đứng là $x=1$ True False

c) Đường thẳng $y=-2$ là tiệm cận ngang của đồ thị hàm số True False

d) Đồ thị hàm số có đúng hai đường tiệm cận True False

Question 18. Cho hàm số $y=\frac{5x+1-\sqrt{x+1}}{x^2-2x}$.

a) Đường thẳng $x=0$ là đường tiệm cận đứng của đồ thị hàm số True False

b) Đường thẳng $y=0$ là đường tiệm cận ngang của đồ thị hàm số True False

c) Đường thẳng $x=2$ là đường tiệm cận đứng của đồ thị hàm số True False

d) Đồ thị hàm số có hai đường tiệm cận ngang True False

Question 19. Cho hàm số $y=\frac{ax+b}{cx+d}$ với $a,b,c \in \mathbb{R}$ có đồ thị là hình bên dưới

a) Hàm số nghịch biến trên khoảng $(1;+\infty)$ và đồng biến trên khoảng $(-\infty;1)$ True False

b) Đồ thị hàm số có đường tiệm cận đứng là $x=1$ True False

c) Đồ thị hàm số có đường tiệm cận ngang là $y=-1$ True False

d) Tổng $a+b+c=5$ True False

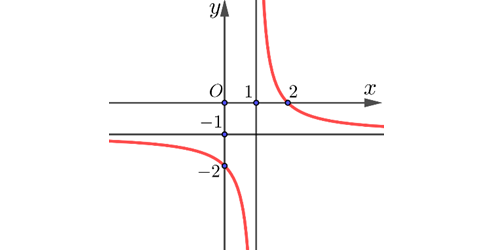
Question 20. Nồng độ oxygen trong hồ theo thời gian $t$ cho bởi công thức $y(t)=5-\frac{15t}{9t^2+1}$, với $y$ được tính theo mg/l và $t$ được tính theo giờ, $t \ge 0$.

a) Đồ thị hàm số $y(t)$ có một đường tiệm cận ngang và một đường tiệm cận xiên True False

b) Đồ thị hàm số có đường tiệm cận ngang là $y=5$ True False

c) Đồ thị hàm số có đường tiệm cận đứng là $x=\frac{1}{3}$ True False

d) Sau một thời gian đủ dài, nồng độ oxygen trong hồ sẽ bão hòa và đạt ngưỡng 5 mg/l True False

Question 21. Cho hàm số $y=\frac{x^2-2x+2}{x+2}$. Các mệnh đề sau đúng hay sai?

a) Hàm số có hai tiệm cận True False

b) Giao điểm của hai tiệm cận là $I(-2;-6)$ True False

c) Khoảng cách từ $O$ đến tiệm cận xiên bằng $4\sqrt{2}$ True False

d) Tiệm cận xiên của hàm số đi qua điểm $M(0;-4)$ True False

Question 22. Gọi (C) là đồ thị của hàm số $y=\frac{mx^2+(3-m)x+m^2-2}{x-1}$, $m$ là tham số. Khi (C) có tiệm cận xiên, gọi đường tiệm cận xiên này là $(d)$. Các mệnh đề sau đúng hay sai?

a) Khi $m=2$ thì $(d)$ có phương trình là $y=2x+3$ True False

b) Khi $m=1$ thì $(d)$ đi qua điểm $A(1;4)$ True False

c) Có 1 đường thẳng $(d)$ tạo với hai trục tọa độ một tam giác có diện tích bằng 6 True False

d) Khi $m=\pm\sqrt{3}$ thì khoảng cách từ gốc tọa độ $O$ đến $(d)$ bằng $\sqrt{3}$ True False

Question 23. Cho hàm số $y=\frac{x^2+mx-1}{x-1}$ ($C_m$) ($m$ là tham số). Các mệnh đề sau đúng hay sai?

a) Để đồ thị ($C_m$) của hàm số có tiệm cận xiên thì $m \neq 0$ True False

b) Để tiệm cận xiên của ($C_m$) đi qua $M(2;-5)$ thì $m=-8$ True False

c) Để tiệm cận xiên của ($C_m$) tạo với hai trục toạ độ một tam giác có diện tích bằng 8 (đvdt) thì tổng tất cả các giá trị $m$ tìm được bằng 2 True False

d) Với $m=3$ thì giao điểm của hai đường tiệm cận của ($C_m$) nằm trên Parabol $y=x^2+3$ True False

📋 Danh sách slide