Question 1. Cho hàm số $y = \frac{3x-2}{x+1}$. Giả sử đồ thị hàm số có đường tiệm cận đứng là $x=a$ và đường tiệm cận ngang là $y=b$. Tính giá trị $a+b$.

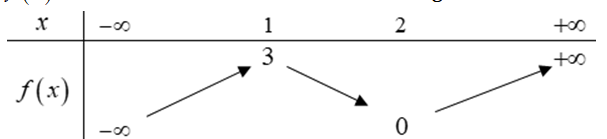
Question 2. Cho hàm số có bảng biến thiên bên dưới. Khi đó, đồ thị hàm số có số đường tiệm cận là bao nhiêu?

Question 3. Cho hàm số $y = f(x) = \frac{x^2-5x+7}{x-3}$ có đồ thị (C). Đường tiệm cận xiên của đồ thị (C) là đường thẳng $\Delta: y = ax+b$. Tính $a+b$.

Question 4. Đường tiệm cận xiên của đồ thị hàm số $y=\frac{2x^2-5x+1}{2x+1}$ cắt các trục tọa độ tại hai điểm $A$ và $B$. Diện tích tam giác $OAB$ bằng bao nhiêu? Kết quả được làm tròn đến hàng phần chục.

Question 5. Khoảng cách từ gốc tọa độ $O$ đến tiệm cận xiên của đồ thị hàm số $f(x) = \frac{2x^3-x^2}{x^2+1}$ bằng $d$. Tính $d^2$ theo dạng số thập phân.

Question 6. Đường tiệm cận đứng và tiệm cận xiên của đồ thị hàm số $y = \frac{-x^2+4x+3}{2x+1}$ tạo với nhau một góc bằng bao nhiêu độ (làm tròn đến hàng phần chục của độ)?

Question 7. Cho hàm số $y = \frac{x^2+3}{x-2}$ có đồ thị (C). Hai đường tiệm cận của đồ thị (C) cùng với hai trục tọa độ tạo thành một hình thang vuông có diện tích $S$. Tính $S$.

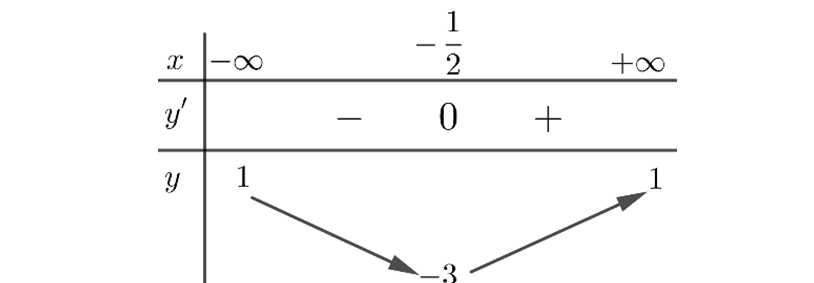
Question 8. Cho hàm số $y=f(x)$ có bảng biến thiên như hình dưới đây.
Tìm tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số $y = \frac{1}{2f(x)-1}$.

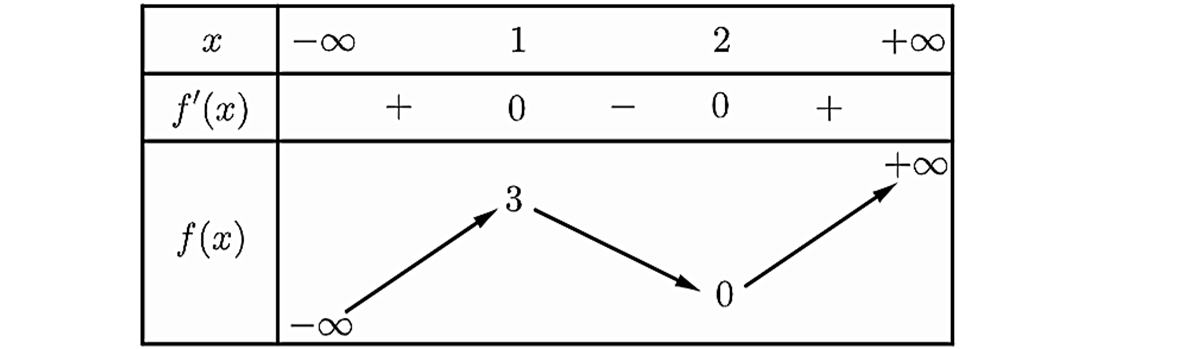
Question 9. Cho hàm số $y=f(x)$ xác định, liên tục trên $\mathbb{R}$ và có bảng biến thiên như hình bên dưới:
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số $y = \frac{1}{2f(x)-1}$ là?

Question 10. Cho hàm số $y = \frac{3x-3}{\sqrt{x^2-1}}$. Gọi $a$ là số đường tiệm cận đứng và $b$ là số đường tiệm cận ngang của đồ thị hàm số đã cho. Giá trị $20a+10b^2$ bằng bao nhiêu?

Question 11. Cho hàm số $y=\frac{x^2-2x+2}{x-1}$ có đồ thị là (C). Gọi $I$ là giao điểm của hai đường tiệm cận của đồ thị (C). Trên đồ thị (C) có một điểm $M(a;b)$ với $a>1$ sao cho khoảng cách $IM$ là nhỏ nhất. Tìm $a$ (làm tròn kết quả đến hàng phần trăm).

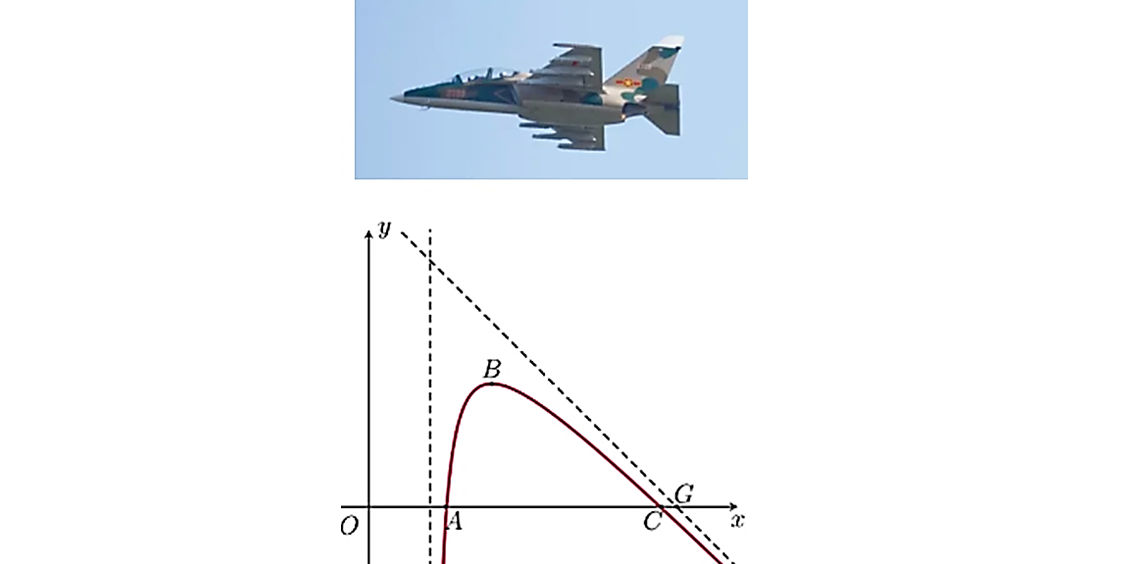
Question 12. Một máy bay trình diễn có đường bay gắn với hệ trục $Oxy$ được mô phỏng như hình vẽ, trục $Ox$ gắn với mặt đất.
Đường bay có dạng là một phần của đồ thị hàm phân thức bậc hai trên bậc nhất $y=f(x)$ có đường tiệm cận đứng là $x=2$. Điểm $G$ là giao điểm của đường tiệm cận xiên của đồ thị hàm số $y=f(x)$ và trục $Ox$ được gọi là điểm giới hạn. Biết máy bay bay từ vị trí $A$ cách tọa tọa độ $O$ một khoảng 2,5 đơn vị và máy bay khi ở vị trí cao nhất cách điểm xuất phát 1,5 đơn vị theo phương song song với trục $Ox$ và cách mặt đất 4,5 đơn vị. Vị trí máy bay tiếp đất cách điểm giới hạn một khoảng bằng bao nhiêu?

Question 13. Cho hàm số $y = \frac{3x-2}{x+1}$. Giả sử đồ thị hàm số có đường tiệm cận đứng là $x=a$ và đường tiệm cận ngang là $y=b$. Tính giá trị $a+b$.

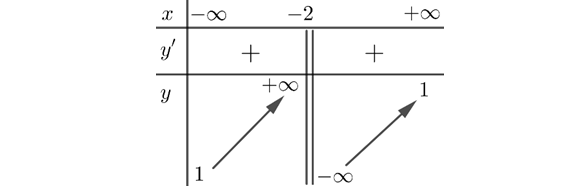
Question 14. Cho hàm số có bảng biến thiên bên dưới. Khi đó, đồ thị hàm số có số đường tiệm cận là bao nhiêu?

Question 15. Cho hàm số $y=f(x)=\frac{x^2-5x+7}{x-3}$ có đồ thị (C). Đường tiệm cận xiên của đồ thị (C) là đường thẳng $\Delta: y=ax+b$. Tính $a+b$.

Question 16. Cho hàm số $y=\frac{x^2+3}{x-2}$ có đồ thị (C). Hai đường tiệm cận của đồ thị (C) cùng với hai trục tọa độ tạo thành một hình thang vuông có diện tích $S$. Tính $S$.

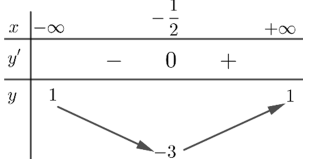
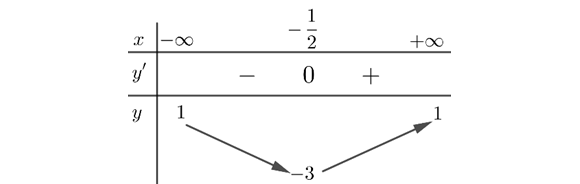
Question 17. Cho hàm số $y=f(x)$ có bảng biến thiên như hình dưới đây.
Tìm tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số $y=\frac{1}{2f(x)-1}$.

Question 18. Cho hàm số $y=\frac{12+\sqrt{4x-x^2}}{\sqrt{x^2-6x+2m}}$ có đồ thị ($C_m$). Tập $S$ tất cả các giá trị của tham số thực $m$ để ($C_m$) có đúng hai tiệm cận đứng có dạng $(a;b)$. Tính $a+2b$.

Question 19. Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số $y=\frac{\sqrt{4x^2-1}+3x^2+2}{x^2-x}$ là?

Question 20. Có bao nhiêu giá trị nguyên của tham số $m$ để đồ thị hàm số $y=\frac{mx^2+(3m+1)x-m+2}{x+1}$ có tiệm cận xiên là $(d)$ và $(d)$ tiếp xúc với đường tròn tâm $I(1;2)$, bán kính bằng $\sqrt{2}$.

Question 21. Tổng các giá trị của tham số $m$ để đồ thị của hàm số $y=\frac{x-1}{x^2+2(m-1)x+m^2-2}$ có đúng một tiệm cận đứng.

Question 22. Cho hàm số $y=f(x)$ xác định, liên tục trên $\mathbb{R}$ và có bảng biến thiên như hình bên dưới:
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số $y=\frac{1}{2f(x)-1}$ là?