LỚP TOÁN THẦY BÌNH

📘 BÀI TIỆM CẬN

Môn Toán - Lớp 12

📘 BÀI TẬP TRẮC NGHIỆM

Question 1. (THPT Đào Duy Từ - Thanh Hóa 2025) Cho hàm số $y=f(x)$ có đồ thị như hình vẽ. Đường thẳng nào sau đây là tiệm cận ngang của đồ thị hàm số đã cho

A.A. $x=1$ B.B. $x=-1$ C.C. $y=1$ D.D. $y=-1$

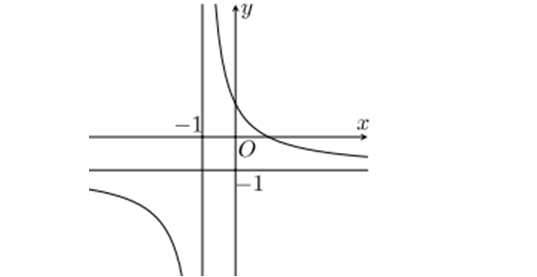
Question 2. (THPT Hàm Rồng - Thanh Hóa 2025) Đường tiệm cận ngang của đồ thị hàm số $y=1+\dfrac{2x+1}{x+2}$ có phương trình là:

A.A. $x=-2$ B.B. $y=3$ C.C. $x=-1$ D.D. $y=2$

Question 3. (Đề Tham Khảo 2025) Cho hàm số $y=\dfrac{ax+b}{cx+d}$ ($c \ne 0, ad-bc \ne 0$) có đồ thị như hình vẽ bên. Tiệm cận ngang của đồ thị hàm số là:

A.A. $x=-1$ B.B. $y=\dfrac{1}{2}$ C.C. $y=-1$ D.D. $x=\dfrac{1}{2}$

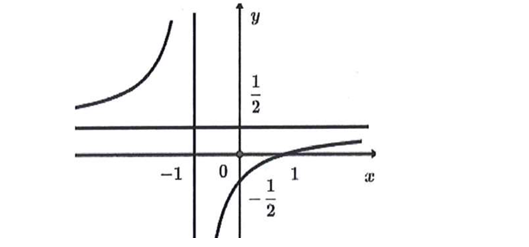
Question 4. (THPT Lương Tài 2 - Bắc Ninh 2025) Đường tiệm cận ngang của đồ thị hàm số $y=\dfrac{4x+1}{2x-2}$ là

A.A. $y=2$ B.B. $x=2$ C.C. $x=1$ D.D. $y=1$

Question 5. (THPT Văn Giang - Hưng Yên 2025) Đường tiệm cận đứng của đồ thị hàm số $y=\dfrac{x-1}{x+2}$ là

A.A. $x=1$ B.B. $x=-1$ C.C. $x=-2$ D.D. $x=2$

Question 6. (THPT Tiên Du - Bắc Ninh 2025) Cho đồ thị hàm số $y=\dfrac{2x^2+x-5}{x+3}$ có đường tiệm cận xiên là đường thẳng $\Delta: y=ax+b$ với $a,b \in \mathbb{R}, a \ne 0$. Giá trị của tổng $a+b$ bằng

A.A. -3 B.B. 7 C.C. 3 D.D. -5

Question 7. (THPT Lê Thánh Tông - HCM 2025) Tiệm cận ngang của đồ thị hàm số $y=\dfrac{2x-3}{x+1}$ là đường thẳng có phương trình

A.A. $y=-1$ B.B. $y=-1$ C.C. $y=2$ D.D. $x=2$

Question 8. (THPT Nguyễn Đăng Đạo - Bắc Ninh 2025) Đường tiệm cận xiên của đồ thị hàm số $y=2x-1+\dfrac{1}{x}$ có phương trình là:

A.A. $y=1-2x$ B.B. $y=2x$ C.C. $y=2x-1$ D.D. $y=-2x$

Question 9. (THPT Gia Bình - Bắc Ninh 2025) Hàm số $y=\dfrac{ax+b}{cx+d}$ ($c \ne 0, ad-bc \ne 0$) có đồ thị dưới đây. Đường tiệm cận đứng của đồ thị hàm số là:

A.A. $x=-1$ B.B. $x=1$ C.C. $x=2$ D.D. $y=-1$

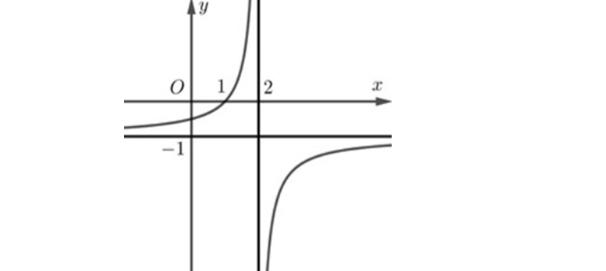
Question 10. (THPT Thạch Thành 1 - Thanh Hóa 2025) Cho hàm số $y=f(x)$ có đồ thị như hình vẽ
Đồ thị hàm số đã cho có bao nhiêu đường tiệm cận?

A.A. 4 B.B. 1 C.C. 3 D.D. 2

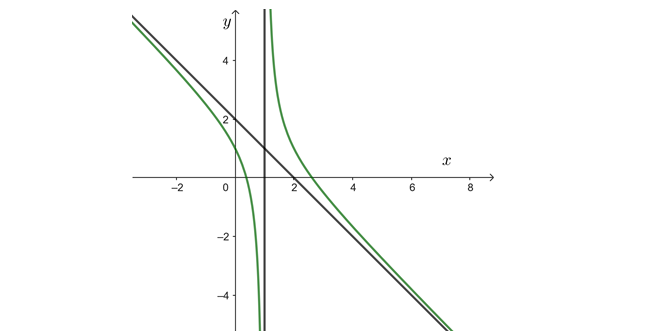
Question 11. (THPT Thạch Thành 1 - Thanh Hóa 2025) Tiệm cận ngang của đồ thị hàm số $y=\dfrac{x-2}{x+1}$ là

A.A. $y=-2$ B.B. $x=2$ C.C. $x=-1$ D.D. $y=1$

Question 12. (THPT Yên Lạc - Vĩnh Phúc 2025) Tiệm cận ngang của đồ thị hàm số $y=\dfrac{3x-2}{x+1}$ là đường thẳng

A.A. $x=-1$ B.B. $y=-2$ C.C. $y=3$ D.D. $x=3$

Question 13. (THPT Chuyên Vĩnh Phúc 2025) Đường tiệm cận ngang của đồ thị hàm số $y=\dfrac{2x+1}{x+1}$ là

A.A. $y=2$ B.B. $x=-1$ C.C. $y=-1$ D.D. $x=2$

Question 14. (Sở Ninh Bình 2025) Cho hàm số $y=\dfrac{ax^2+bx+c}{mx+n}$ (với $a \ne 0; m \ne 0$) có đồ thị như hình vẽ dưới đây.
Phương trình đường tiệm cận xiên của đồ thị hàm số đã cho là:

A.A. $y=2x+2$ B.B. $y=x-2$ C.C. $y=2x-2$ D.D. $y=x+2$

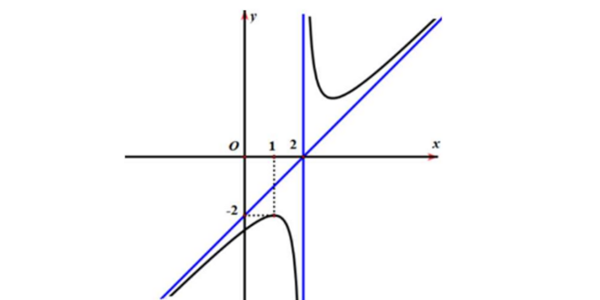
Question 15. (THPT Nguyễn Viết Xuân - Vĩnh Phúc 2025) Tiệm cận xiên của đồ thị hàm số $y=\dfrac{x^2-2x+4}{x-3}$ đi qua điểm nào sau đây?

A.A. $M(2024;2025)$ B.B. $Q(2027;2024)$ C.C. $N(2025;2022)$ D.D. $P(2024;2024)$

Question 16. (THPT Nguyễn Viết Xuân - Vĩnh Phúc 2025) Tiệm cận ngang của đồ thị hàm số $y=\dfrac{4x-5}{2x+1}$ là đường thẳng:

A.A. $y=4$ B.B. $y=-\dfrac{1}{2}$ C.C. $y=2$ D.D. $y=-5$

Question 17. (THPT Triệu Sơn 3 - Thanh Hóa 2025) Tiệm cận đứng của đồ thị hàm số $y=\dfrac{3x+2}{x-2}$ là đường thẳng có phương trình

A.A. $x=2$ B.B. $x=-1$ C.C. $x=3$ D.D. $x=-2$

Question 18. (Cụm trường THPT Hải Dương 2025) Cho hàm số $y=f(x)$ có bảng biến thiên như hình vẽ dưới đây.
Đồ thị hàm số $y=f(x)$ có bao nhiêu đường tiệm cận?

A.A. 3 B.B. 2 C.C. 1 D.D. 4

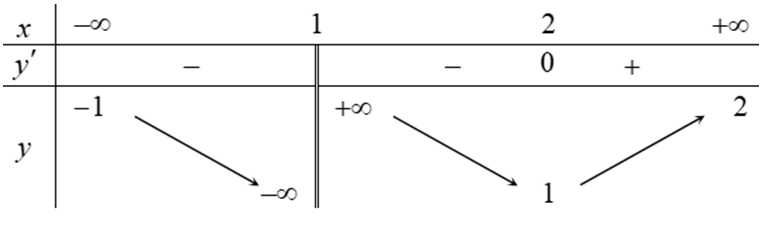
Question 19. (THPT Nguyễn Khuyến - Lê Thánh Tông 2025) Cho hàm số $f(x)$ xác định trên $(-\infty;0) \setminus \{-2\}$ và có bảng biến thiên bên dưới. Đồ thị hàm số đã cho có tổng số đường tiệm cận ngang và tiệm cận đứng là

A.A. 1 B.B. 3 C.C. 0 D.D. 2

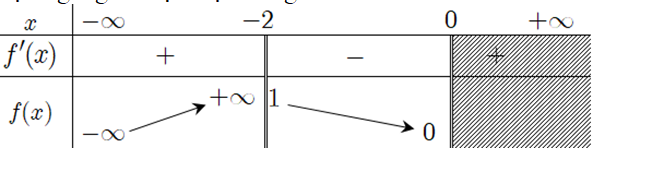
Question 20. (Chuyên Phan Bội Châu - Nghệ An 2025) Đường tiệm cận xiên của đồ thị hàm số $y=\dfrac{x^2+2x-3}{x-2}$ là

A.A. $y=x$ B.B. $x=2$ C.C. $y=2$ D.D. $y=x+4$

Question 21. (Chuyên Phan Bội Châu - Nghệ An 2025) Đường tiệm cận đứng của đồ thị hàm số $y=\dfrac{2x+3}{x-1}$ là

A.A. $x=1$ B.B. $x=2$ C.C. $y=1$ D.D. $y=2$

Question 22. (THPT Kinh Môn - Hải Dương 2025) Tìm phương trình đường tiệm cận ngang của đồ thị hàm số $y=\dfrac{x+2}{1-x}$.

A.A. $x=1$ B.B. $y=-1$ C.C. $y=1$ D.D. $x=-1$

Question 23. (HSG Vũng Tàu 2025) Cho hàm số $y=\sqrt{x^2+2x+2}$. Số đường tiệm cận xiên của đồ thị hàm số là

A.A. 0 B.B. 1 C.C. 2 D.D. 3

Question 24. (THPT Triệu Sơn 1-Thanh Hóa 2025) Cho hàm số $y=f(x)$ xác định trên $\mathbb{R} \setminus \{1\}$, liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình bên dưới. Hỏi đồ thị hàm số đã cho có tất cả bao nhiêu đường tiệm cận đứng và đường tiệm cận ngang?

A.A. 1 B.B. 2 C.C. 3 D.D. 4

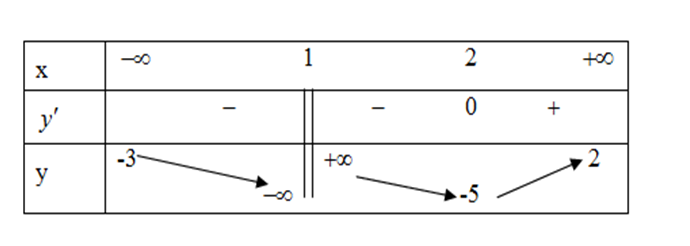
Question 25. (THPT Cụm trường Hải Dương 2025) Đồ thị hàm số $y=\dfrac{x^2+2x+2}{x+1}$ có tiệm cận xiên là đường thẳng

A.A. $y=x$ B.B. $y=2x-1$ C.C. $y=x-1$ D.D. $y=x+1$

Question 26. (THPT Lê Xoay - Vĩnh Phúc 2025) Cho hàm số $y=\dfrac{ax+b}{cx+d} (ad-bc \ne 0; c \ne 0)$ có bảng biến thiên như sau
Đồ thị hàm số có đường tiệm cận đứng là

A.A. $y=-1$ B.B. $y=2$ C.C. $x=2$ D.D. $x=-1$

Question 27. (THPT Diễn Châu 5 - Nghệ An 2025) Tiệm cận đứng và tiệm cận ngang của đồ thị hàm số $y=\dfrac{2x-1}{x+1}$ có phương trình lần lượt là:

A.A. $x=-1, y=2$ B.B. $x=\dfrac{1}{2}, y=-1$ C.C. $x=1, y=-2$ D.D. $x=-1, y=\dfrac{1}{2}$

Question 28. (THPT Lê Lợi - Thanh Hóa 2025) Đường tiệm cận đứng của đồ thị hàm số $y=\dfrac{x-1}{x+2}$ là

A.A. $x=1$ B.B. $x=-1$ C.C. $x=-2$ D.D. $x=2$

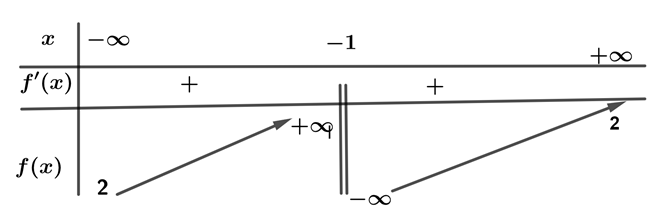
Question 29. (THPT Triệu Sơn 4 - Thanh Hóa 2025) Cho hàm số $y=f(x)$ có bảng biến thiên như sau:
Tiệm cận đứng của đồ thị hàm số đã cho là đường thẳng có phương trình:

A.A. $x=-1$ B.B. $x=-2$ C.C. $y=-1$ D.D. $y=-2$

Question 30. (THPT Triệu Sơn 4 - Thanh Hóa 2025) Cho hàm số $y=\dfrac{ax+b}{cx+d} (c \ne 0, ad-bc \ne 0)$ có đồ thị như hình vẽ bên. Tiệm cận đứng của đồ thị hàm số là:

A.A. $x=-1$ B.B. $y=-1$ C.C. $x=1$ D.D. $y=1$

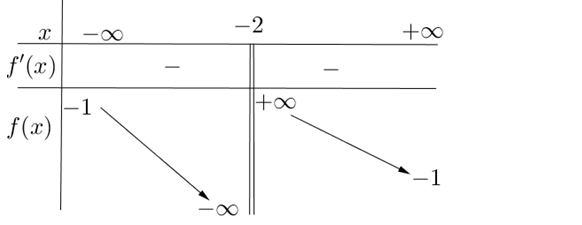
Question 31. (Cụm trường THPT Bắc Ninh 2025) Cho hàm số $y=f(x)$ xác định trên $\mathbb{R} \setminus \{1\}$, liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:
Hỏi đồ thị hàm số đã cho có tất cả bao nhiêu đường tiệm cận đứng:

A.A. 4 B.B. 2 C.C. 3 D.D. 1

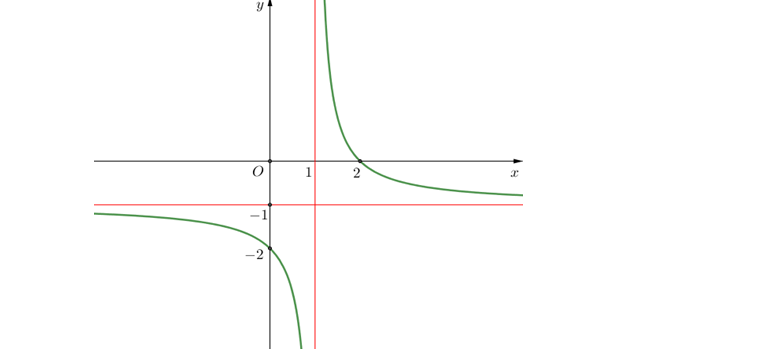
Question 32. (Sở Hà Tĩnh 2025) Cho hàm số $y=\dfrac{ax^2+bx+c}{x}, (ac \ne 0)$ có đồ thị như hình vẽ. Đường tiệm cận xiên của đồ thị hàm số đã cho là đường thẳng có phương trình

A.A. $y=x$ B.B. $y=-x$ C.C. $x=0$ D.D. $y=2x$

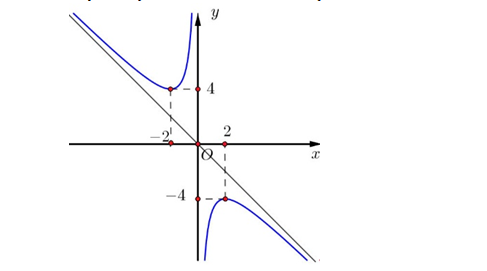
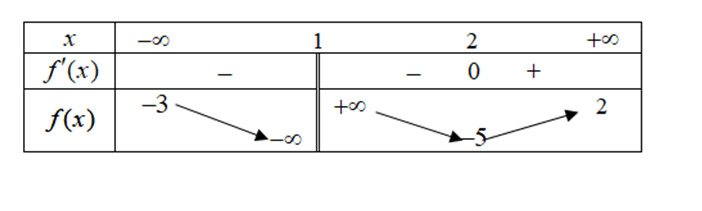
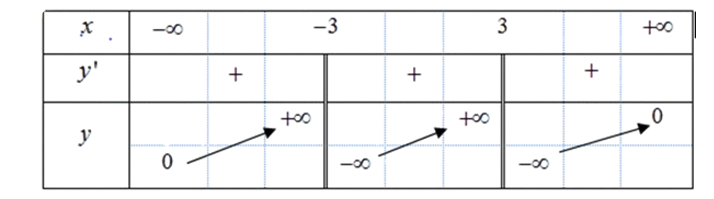
Question 33. (THPT Cẩm Xuyên - Hà Tĩnh 2025) Cho hàm số $y=f(x)$ có bảng biến như sau:
Số đường tiệm cận đứng của đồ thị hàm số là

A.A. 4 B.B. 3 C.C. 2 D.D. 1

Question 34. (Chuyên KHTN Hà Nội 2025) Đường tiệm cận xiên của đồ thị hàm số $y=\dfrac{x^2-2x}{x+1}$ có phương trình là

A.A. $y=x-1$ B.B. $y=x-3$ C.C. $y=x+1$ D.D. $y=x$

Question 35. (Chuyên Hạ Long 2025) Cho hàm số $y=\dfrac{ax+b}{cx+d}$ ($c \ne 0; ad-bc \ne 0$) có đồ thị như hình vẽ.
Tiệm cận ngang của đồ thị hàm số đã cho là

A.A. $x=2$ B.B. $y=1$ C.C. $y=2$ D.D. $x=2$

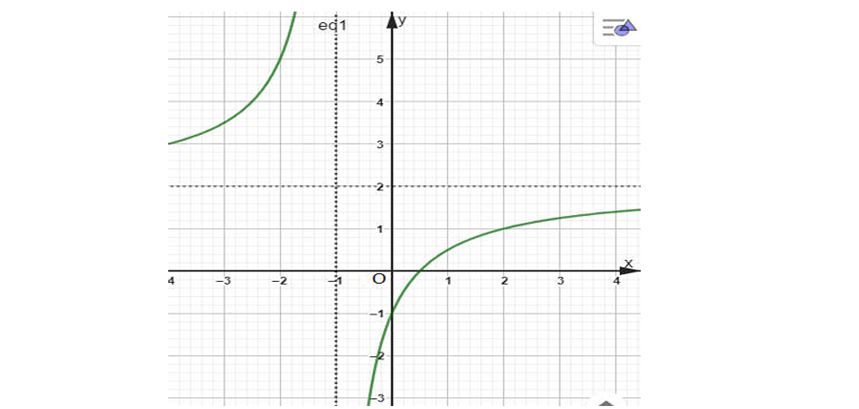
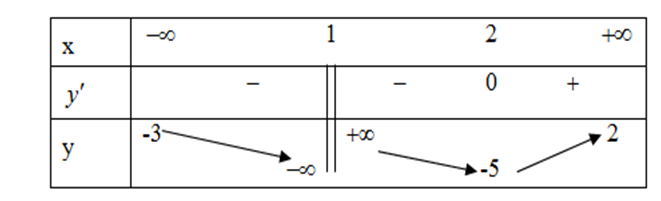
Question 36. (Chuyên Thái Bình 2025) Tiệm cận xiên của đồ thị hàm số $y=\dfrac{x^2-2x+4}{x-3}$ đi qua điểm nào sau đây?

A.A. $M(1;2)$ B.B. $Q(1;-3)$ C.C. $N(3;1)$ D.D. $P(2;2)$

Question 37. (Chuyên Thái Bình 2025) Cho hàm số $y=f(x)$ xác định trên $\mathbb{R} \setminus \{1\}$, liên tục trên mỗi khoảng xác định và có bảng biến thiên như hình bên dưới. Hỏi đồ thị hàm số đã cho có tất cả bao nhiêu đường tiệm cận đứng và đường tiệm cận ngang?

A.A. 1 B.B. 2 C.C. 3 D.D. 4

Question 38. (Chuyên Vinh 2025) Cho hàm số $y=\dfrac{ax^2+bx+c}{mx+n}$ có đồ thị như hình bên.
Tiệm cận xiên của đồ thị hàm số đã cho là

A.A. $y=-x+1$ B.B. $y=x-1$ C.C. $y=-x-1$ D.D. $y=x+1$

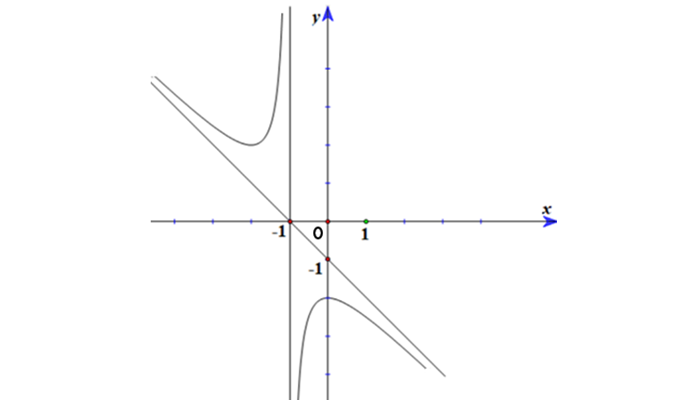
Question 39. (Sở Thanh Hóa 2025) Cho hàm số $y=\dfrac{ax+b}{cx+d}$ ($c \ne 0; ad-bc \ne 0$) có đồ thị như hình vẽ bên dưới.
Đồ thị hàm số có đường tiệm cận ngang là:

A.A. $y=0$ B.B. $y=-1$ C.C. $x=-1$ D.D. $y=1$

Question 40. (THPT Trần Phú - Vĩnh Phúc 2025) Đường tiệm cận ngang của đồ thị hàm số $y=\dfrac{2x+1}{x+1}$ là

A.A. $y=2$ B.B. $x=-1$ C.C. $x=2$ D.D. $y=-1$

Question 41. (Sở Vĩnh Phúc 2025) Tiệm cận ngang của đồ thị hàm số $y=\dfrac{3x+1}{x+1}$ là

A.A. $y=-1$ B.B. $x=2$ C.C. $y=3$ D.D. $x=-1$

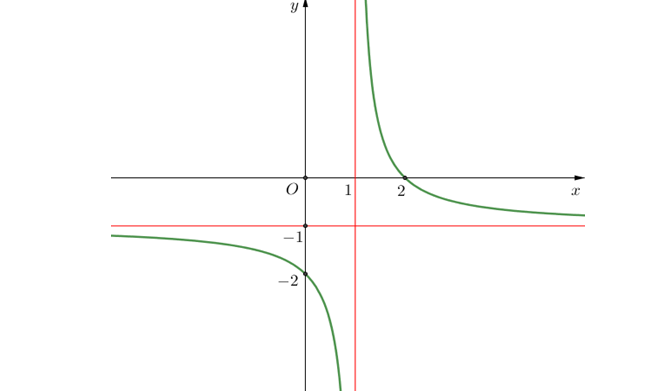
Question 42. (Cụm trường Hải Dương 2025) Đồ thị dưới đây là của hàm số nào trong các hàm số cho ở các phương án A,B,C,D?

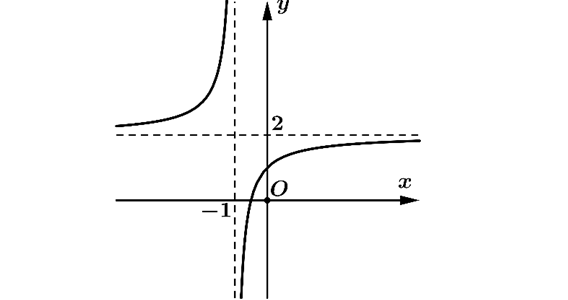
A.A. $y=\dfrac{2x+1}{x+1}$ B.B. $y=\dfrac{2x-1}{x-1}$ C.C. $y=2x+\dfrac{1}{x+1}$ D.D. $y=x^3-3x+1$

Question 43. (Sở Thừa Thiên Huế 2025) Cho hàm số $y=\dfrac{ax+b}{cx+d}$ ($c \ne 0, ad-bc \ne 0$) có đồ thị như hình sau:
Đường thẳng nào sau đây là đường tiệm cận đứng của đồ thị hàm số đã cho?

A.A. $x=1$ B.B. $x=2$ C.C. $y=1$ D.D. $y=2$

Question 44. (Chuyên Lê Khiết - Quảng Ngãi 2025) Cho hàm số $y=\dfrac{2x+3}{x+1}$. Tiệm cận đứng của đồ thị hàm số này là

A.A. $y=\dfrac{1}{2}$ B.B. $y=-1$ C.C. $x=-\dfrac{1}{2}$ D.D. $x=-1$

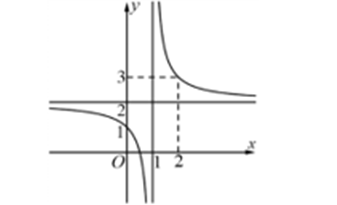
Question 45. (Cụm trường Nguyễn Hiền - Lê Hồng Phong - Quảng Nam 2025) Cho hàm số $y=f(x)$ có đồ thị như hình bên dưới. Khẳng định nào sau đây là đúng?

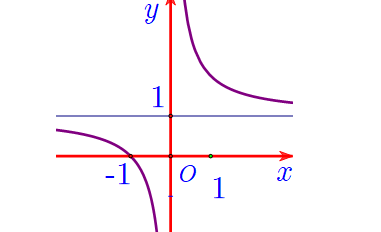
A.A. Đồ thị hàm số có tiệm cận đứng $x=0$, không có tiệm cận ngang B.B. Đồ thị hàm số có tiệm cận ngang $y=0$, có tiệm cận đứng $x=1$ C.C. Đồ thị hàm số có tiệm cận ngang $y=0$, không có tiệm cận đứng D.D. Đồ thị hàm số có tiệm cận đứng $x=0$, tiệm cận ngang $y=1$

Question 46. (Cụm trường Nguyễn Hiền - Lê Hồng Phong - Quảng Nam 2025) Tìm tiệm cận xiên (d) của đồ thị hàm số $y=\dfrac{-x^2+2x+5}{x+1}$

A.A. $(d) y=-x+1$ B.B. $(d) y=-x-1$ C.C. $(d) y=-x+3$ D.D. $(d) y=x+3$

Question 47. (THPT Nông Cống 3 - Thanh Hóa 2025) Cho hàm số $y=f(x)$ có bảng biến thiên như sau
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho bằng

A.A. 3 B.B. 2 C.C. 1 D.D. 0

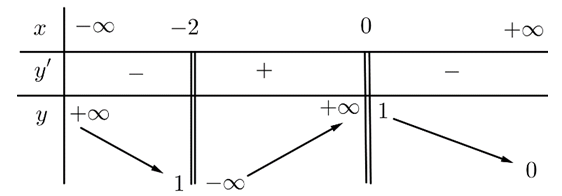
Question 48. (THPT Anh Sơn 3 - Nghệ An 2025) Cho hàm số $y=f(x)$ có bảng biến thiên như sau:
Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là

A.A. 4 B.B. 2 C.C. 1 D.D. 3

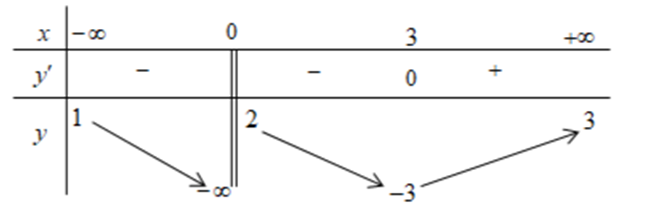
Question 49. (THPT Lê Thánh Tông - Nguyễn Khuyến HCM 2025) Đường thẳng $y=-2x+1$ là tiệm cận xiên của đồ thị hàm số nào dưới đây?

A.A. $y=-2x+1-\dfrac{3}{x-2}$ B.B. $y=x+1+\dfrac{1}{-2x+1}$ C.C. $y=3x-2+\dfrac{3}{2x-1}$ D.D. $y=\dfrac{1}{-2x+1}$

Question 50. (Sở Bắc Giang 2025) Cho hàm số $y=f(x)$ có đồ thị như hình vẽ dưới đây
Tiệm cận ngang của đồ thị hàm số là đường thẳng có phương trình

A.A. $x=1$ B.B. $y=1$ C.C. $x=-\dfrac{1}{2}$ D.D. $y=-\dfrac{1}{2}$

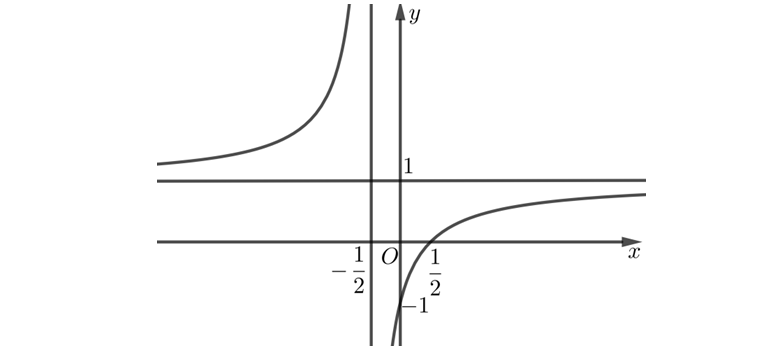
Question 51. (Sở Phú Thọ 2025) Cho hàm số $f(x)=\dfrac{ax^2+bx+c}{dx+e} (a,b,c,d,e \in \mathbb{R}, ad \ne 0)$ có đồ thị như hình vẽ.
Tiệm cận xiên của đồ thị hàm số đã cho là

A.A. $y=-x$ B.B. $y=x$ C.C. $y=x-1$ D.D. $y=x+1$

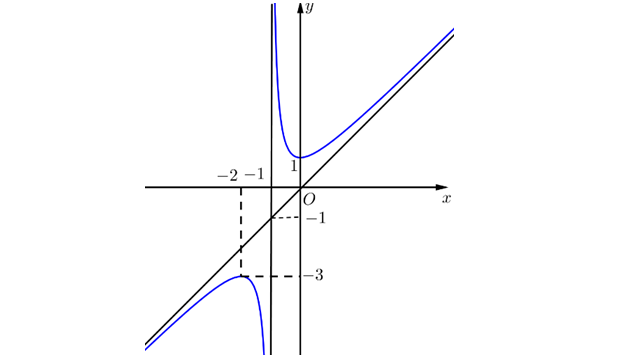
Question 52. (Sở Ninh Bình 2025) Cho hàm số $y=\dfrac{ax+b}{cx+d}$ (với $c \ne 0; ad-bc \ne 0$) có đồ thị như hình vẽ dưới đây.
Đường tiệm cận đứng của đồ thị hàm số đã cho có phương trình là:

A.A. $x-2=0$ B.B. $x+1=0$ C.C. $y+1=0$ D.D. $y-2=0$

Question 53. (THPT Sào Nam - Quảng Nam 2025) Cho đồ thị hàm số $y=\dfrac{x^2+3x-5}{x+3}$ có đường tiệm cận xiên là đường thẳng $\Delta: y=ax+b$ và tiệm cận đứng là đường thẳng $\Delta':x=c$ với $a,b,c \in \mathbb{R}$. Giá trị của tổng $S=a+b+c$ bằng

A.A. $S=-1$ B.B. $S=-2$ C.C. $S=1$ D.D. $S=4$

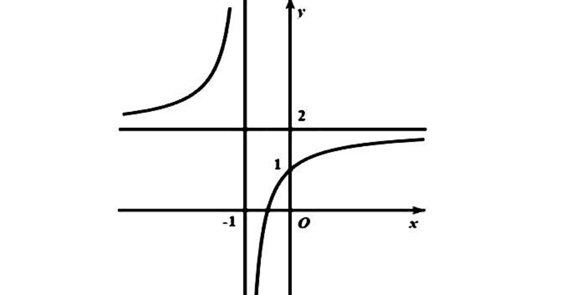
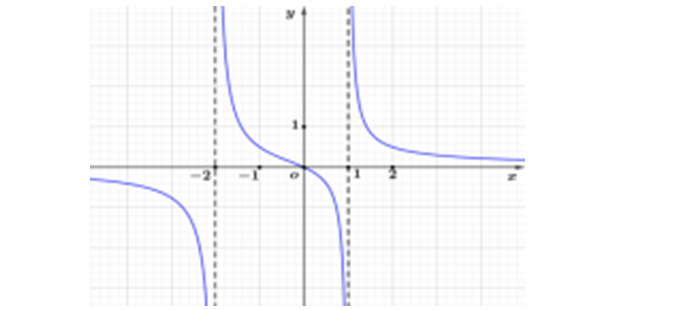
Question 54. (Cụm trường THPT Hải Dương 2025) Cho hàm số $y=f(x)$ có đồ thị như sau:
Tiệm cận đứng của đồ thị hàm số đã cho là:

A.A. $y=1$ và $y=-2$ B.B. $x=1$ và $x=-2$ C.C. $y=0$ D.D. $x=0$

Question 55. (THPT Trực Ninh - Nam Định 2025) Phương trình đường tiệm cận ngang của đồ thị hàm số $y=\dfrac{x+2}{-x+1}$ là

A.A. $x=1$ B.B. $y=1$ C.C. $x=-1$ D.D. $y=-1$

Question 56. (Sở Thái Nguyên 2025) Đường tiệm cận xiên của đồ thị hàm số $y=\dfrac{x^2+4x-7}{x-2}$ là

A.A. $y=x-6$ B.B. $y=-x-6$ C.C. $y=-x+6$ D.D. $y=x+6$

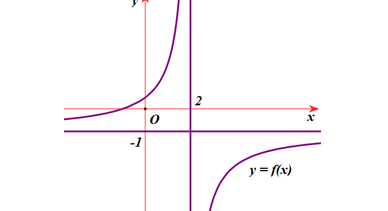
Question 57. (Chuyên Lê Quý Đôn - Đà Nẵng 2025) Cho hàm số $y=f(x)$ thỏa mãn: $\lim_{x \to 1^+} f(x)=2; \lim_{x \to -1^-} f(x)=-\infty; \lim_{x \to +\infty} f(x)=0$ và $\lim_{x \to -\infty} f(x)=0$. Khẳng định nào sau đây đúng?

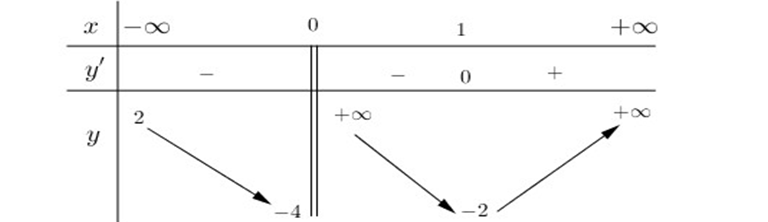
A.A. Đường thẳng $x=0$ là tiệm cận đứng của đồ thị hàm số đã cho B.B. Đường thẳng $y=0$ là tiệm cận ngang của đồ thị hàm số đã cho C.C. Đường thẳng $y=2$ là tiệm cận ngang của đồ thị hàm số đã cho D.D. Đường thẳng $x=-1$ là tiệm cận đứng của đồ thị hàm số đã cho

Question 58. (THPT Lê Hồng Phong - Hải Phòng 2025) Cho hàm số $y=f(x)$ có bảng biến thiên như sau:
Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số đã cho là

A.A. 2 B.B. 4 C.C. 1 D.D. 3

Question 59. (Sở Quảng Bình 2025) Cho hàm số $y=\dfrac{ax+b}{cx+d}$ ($c \ne 0; ad-bc \ne 0$) có đồ thị như hình vẽ bên. Tiệm cận đứng của đồ thị hàm số đã cho là

A.A. $y=-1$ B.B. $y=2$ C.C. $x=-1$ D.D. $x=2$

Question 60. (Sở Bạc Liêu 2025) Tiệm cận ngang của đồ thị hàm số $y=\dfrac{x-2}{x+1}$ là

A.A. $x=1$ B.B. $y=-2$ C.C. $x=-1$ D.D. $y=1$

Question 61. (THPT Lê Thánh Tông - Nguyễn Khuyến 2025) Số đường tiệm cận của đồ thị hàm số $y=\dfrac{3x+4}{x-1}$ bằng:

A.A. 2 B.B. 3 C.C. 1 D.D. 0

Question 62. (Sở Hà Nội 2025) Tiệm cận xiên của đồ thị hàm số $y=x-1-\dfrac{2}{x+1}$ là đường thẳng có phương trình

A.A. $y=x-1$ B.B. $y=-x-1$ C.C. $y=x+1$ D.D. $y=-x+1$

Question 63. (Chuyên KHTN Hà Nội 2025) Đường tiệm cận xiên của đồ thị hàm số $y=\dfrac{2x^2-x+2}{x+1}$ có phương trình là

A.A. $y=2x-3$ B.B. $y=2x+3$ C.C. $y=x+1$ D.D. $y=2x-1$

Question 64. (Sở Tuyên Quang 2025) Đồ thị hàm số $y=2x+1-\dfrac{3}{x+1}$ có đường tiệm cận xiên là:

A.A. $y=2x-3$ B.B. $y=2x+1$ C.C. $y=2x-1$ D.D. $y=x+1$

Question 65. (Sở Yên Bái 2025) Cho hàm số $y=f(x)$ xác định trên khoảng $(-2;1)$ và có $\lim_{x \to (-2)^+} f(x)=2, \lim_{x \to 1^+} f(x)=-\infty$. Khẳng định nào sau đây là đúng?

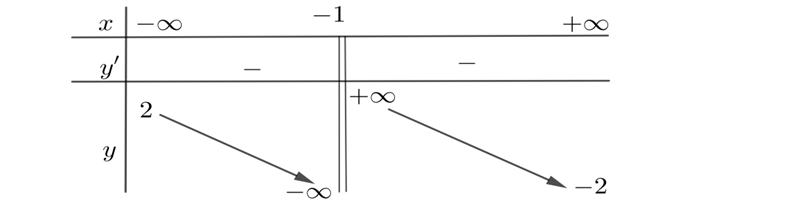
A.A. Đồ thị hàm số $y=f(x)$ có một tiệm cận ngang là đường thẳng $y=2$ B.B. Đồ thị hàm số $y=f(x)$ có một tiệm cận đứng là đường thẳng $x=1$ và một tiệm cận ngang là đường thẳng $y=2$ C.C. Đồ thị hàm số $y=f(x)$ không có tiệm cận D.D. Đồ thị hàm số $y=f(x)$ có đúng một tiệm cận đứng là đường thẳng $x=1$

Question 66. (Chuyên Phan Bội Châu - Hà Tĩnh 2025) Cho hàm số $y=f(x)$ xác định trên $\mathbb{R} \setminus \{-1\}$ có bảng biến thiên như hình bên
Đồ thị hàm số $y=f(x)$ có bao nhiêu đường tiệm cận ngang?

A.A. 0 B.B. 2 C.C. 3 D.D. 1

Question 67. (Sở Bắc Ninh 2025) Đường tiệm cận xiên của đồ thị hàm số $y=\dfrac{x^2-9x-6}{x}$ có phương trình là

A.A. $y=2x-18$ B.B. $y=x-9$ C.C. $y=x+9$ D.D. $y=x-9$

Question 68. (Sở Đà Nẵng 2025) Đồ thị hàm số $y=-x+2+\dfrac{1}{x}$ có đường tiệm cận xiên là

A.A. $y=-x+2$ B.B. $y=\dfrac{1}{x}$ C.C. $y=x-2$ D.D. $y=-\dfrac{1}{x}$

Question 69. ((Sở Hòa Bình 2025) Đồ thị hàm số $y=f(x)=\dfrac{x^2+2x-3}{x+1}$ có đường tiệm cận xiên là

A.A. $y=x+3$ B.B. $y=x+1$ C.C. $y=x-1$ D.D. $y=-x+1$

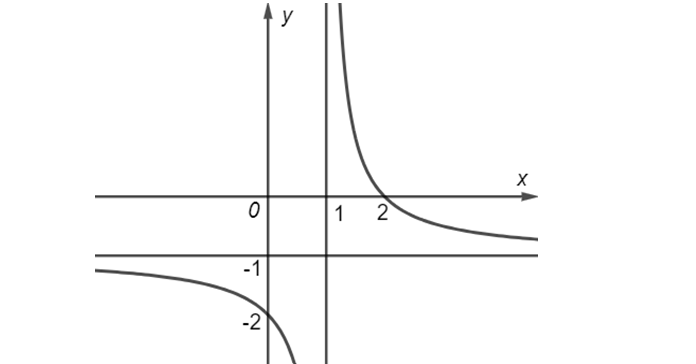
Question 70. (Sở Sơn La 2025) Cho hàm số $y=f(x)$ có đồ thị như hình vẽ dưới đây:
Đồ thị hàm số đã cho có đường tiệm cận đứng là đường thẳng

A.A. $x=1$ B.B. $x=0$ C.C. $x=-1$ D.D. $y=-1$

Question 71. (THPT Hương Hóa - Quảng Trị 2025) Cho hàm số $y=f(x)$ có $\lim_{x \to +\infty} f(x)=1$ và $\lim_{x \to -\infty} f(x)=-1$. Khẳng định nào sau đây đúng?

A.C.Đồ thị hàm số đã cho có đúng một tiệm cận ngang B.D.Đồ thị hàm số đã cho không có tiệm cận ngang C.C. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng $x=1$ và $x=-1$ D.D. Đồ thị hàm số đã cho có hai tiệm cận ngang là các đường thẳng $y=1$ và $y=-1$

Question 72. (THPT Lê Thánh Tông - HCM 2025) Số đường tiệm cận của đồ thị hàm số $y=\dfrac{\sqrt{x^2-4}}{x^2-1}$ là

A.A. 1 B.B. 2 C.C. 3 D.D. 4

Question 73. (Sở Lào Cai 2025) Phương trình đường tiệm cận ngang của đồ thị hàm số $y=\dfrac{-2x-1}{x-2}$ là

A.A. $y=-2$ B.B. $y=2$ C.C. $x=2$ D.D. $x=-2$

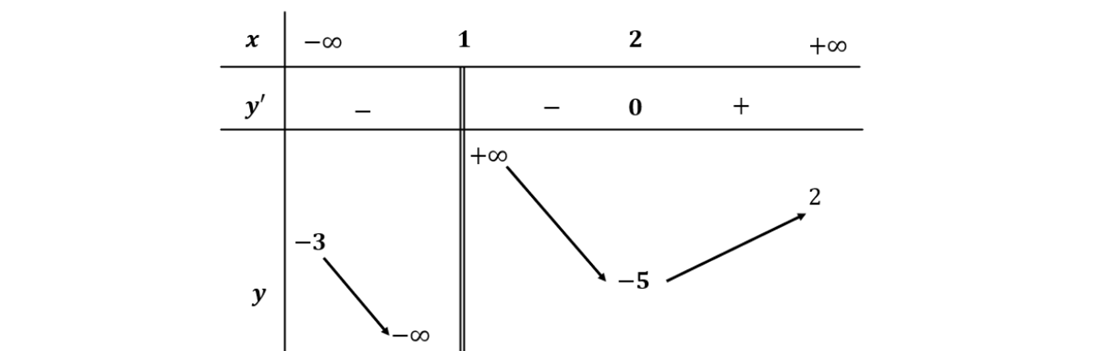
Question 74. (Sở Quảng Nam 2025) Cho hàm số $y=f(x)$ xác định trên $\mathbb{R} \setminus \{1\}$, liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:
Tiệm cận đứng của đồ thị hàm số đã cho là

A.A. $x=2$ B.B. $x=1$ C.C. $y=-3$ D.D. $y=2$

Question 75. (Sở Long An 2025) Cho hàm số $y=\dfrac{ax+b}{cx+d}$ ($c \ne 0, ad-bc \ne 0$) có đồ thị như hình vẽ bên.
Tiệm cận ngang của đồ thị hàm số là:

A.A. $x=-2$ B.B. $y=1$ C.C. $x=1$ D.D. $y=-2$

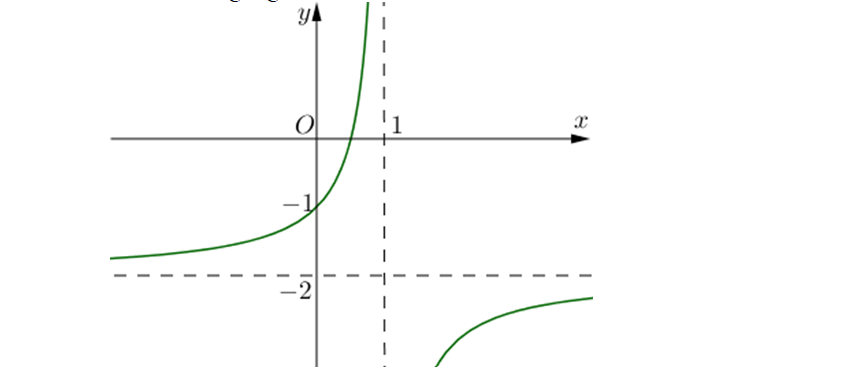
Question 76. (THPT Ngô Sĩ Liên - Bắc Giang 2025) Đường thẳng $2y+1=0$ là tiệm cận ngang của đồ thị hàm số nào sau đây?

A.A. $y=\dfrac{3-x^2}{2x^2-3x+1}$ B.B. $y=\dfrac{x^2+x+1}{1-2x}$ C.C. $y=\dfrac{x+1}{2x+1}$ D.D. $y=\dfrac{2x+1}{1-x}$

Question 77. (Sở Quảng Ninh 2025) Cho hàm số $y=2x-1-\dfrac{3}{x+2}$. Đường tiệm cận xiên của đồ thị hàm số đã cho là:

A.A. $y=-2x+1$ B.B. $y=2x-1$ C.C. $y=2x+1$ D.D. $y=-2x-1$

Question 78. (THPT Hoằng Hóa 2-Thanh Hóa 2025) Cho hàm số $y=f(x)$ liên tục trên $\mathbb{R}$ và có bảng biến thiên như sau
Đồ thị hàm số $y=\dfrac{1}{2f(x)+3}$ có bao nhiêu đường tiệm cận đứng?

A.A. 3 B.B. 4 C.C. 2 D.D. 6

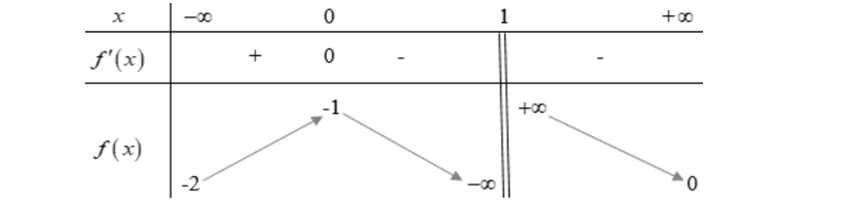
Question 79. (Đề thi vào ĐHSPHN 2025) Đồ thị hàm số $y=\dfrac{-x^2+4x-3}{x+2}$ có đường tiệm cận xiên là:

A.A. Đường thẳng $y=-1$ B.B. Đường thẳng $y=-x+6$ C.C. Đường thẳng $x=-2$ D.D. Đường thẳng $y=-x$

Question 80. (Cụm Ninh Giang - Tứ Kỳ - Gia Lộc 2025) Đồ thị của hàm số $y=\dfrac{x-2}{x^2-4}$ có tất cả bao nhiêu đường tiệm cận đứng và tiệm cận ngang?

A.A. 0 B.B. 1 C.C. 2 D.D. 3

Question 81. (THPT Tư Nghĩa 1 - Quảng Ngãi 2025) Số đường tiệm cận của đồ thị hàm số $y=\dfrac{5x^2+8x+2}{2x^2-2}$ là

A.A. 2 B.B. 1 C.C. 0 D.D. 3

Question 82. (THPT Quế Võ 1 - Bắc Ninh 2025) Đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số $y=\dfrac{2x+3}{x-4}$ tạo với hai trục tọa độ một hình chữ nhật có diện tích bằng

A.A. 8 B.B. 4 C.C. 2 D.D. 6

Question 83. (THPT Quế Võ 1 - Bắc Ninh 2025) Cho hàm số $y=f(x)$ liên tục trên $(a;b)$. Điều kiện cần và đủ để hàm số liên tục trên $[a;b]$ là

A.A. $\lim_{x \to a^+} f(x)=f(a)$ và $\lim_{x \to b^+} f(x)=f(b)$ B.B. $\lim_{x \to a^-} f(x)=f(a)$ và $\lim_{x \to b^-} f(x)=f(b)$ C.C. $\lim_{x \to a^-} f(x)=f(a)$ và $\lim_{x \to b^+} f(x)=f(b)$ D.D. $\lim_{x \to a^+} f(x)=f(a)$ và $\lim_{x \to b^-} f(x)=f(b)$

Question 84. (THPT Triệu Quang Phục - Hưng Yên 2025) Tiệm cận ngang của đồ thị hàm số $f(x)=\dfrac{1-4x}{2x-1}$ là đường thẳng có phương trình là

A.A. $y=2$ B.B. $y=4$ C.C. $y=\dfrac{1}{2}$ D.D. $y=-2$

Question 85. (THPT Triệu Quang Phục - Hưng Yên 2025) Tổng số các đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số $y=\dfrac{\sqrt{9-x^2}-2}{x^2-5}$ là

A.A. 4 B.B. 3 C.C. 2 D.D. 0

Question 86. (Cụm Chương Mỹ - Thanh Oai 2025) Cho hàm số $y=f(x)$ có đồ thị hàm số như hình sau:
Đường tiệm cận xiên của đồ thị hàm số là

A.A. $y=x-1$ B.B. $y=2-x$ C.C. $y=x$ D.D. $y=x+1$

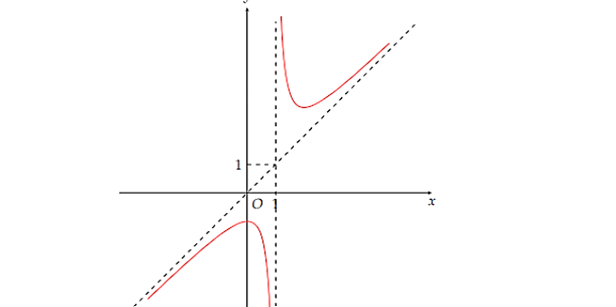
Question 87. (Cụm Chuyên Môn Đăk Lak 2025) Đồ thị của hàm số $y=\dfrac{x+3}{x-1}$ có đường tiệm cận đứng là?

A.A. $y=1$ B.B. $x=1$ C.C. $x=-1$ D.D. $x=-3$

Question 88. (THPT Hà Trung - Thanh Hóa 2025) Cho hàm số $y=f(x)$ xác định trên $\mathbb{R} \setminus \{0\}$ liên tục trên mỗi khoảng xác định và có bảng biến thiên sau.
Hỏi đồ thị hàm số đã cho có bao nhiêu đường tiệm cận?

A.A. 2 B.B. 4 C.C. 5 D.D. 3

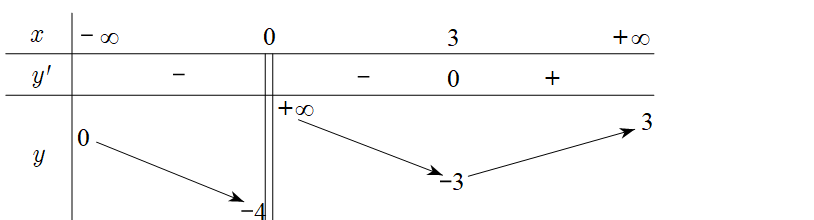
Question 89. (Sở Bắc Ninh 2025) Đường thẳng nào là đường tiệm cận đứng của đồ thị hàm số $y=\dfrac{5x-1}{x+2}$?

A.A. $x=5$ B.B. $y=5$ C.C. $x=2$ D.D. $x=-2$

Question 90. (Sở Bình Phước 2025) Cho hàm số $y=f(x)=\dfrac{ax+b}{cx+d}$ ($c \ne 0, ad-bc \ne 0$) có bảng biến thiên như sau:
Tiệm cận đứng của đồ thị hàm số là

A.A. $x=-2$ B.B. $y=-1$ C.C. $x=-1$ D.D. $y=-2$

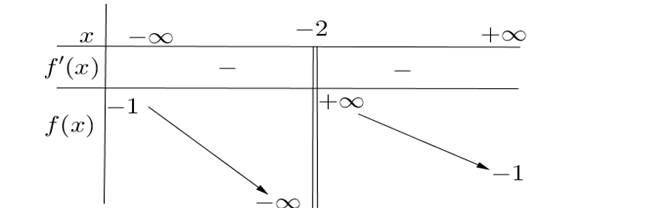
Question 91. (Chuyên Lương Thế Vinh - Đồng Nai 2025) Cho hàm số $y=f(x)$ có bảng biến thiên như sau
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là

A.A. 4 B.B. 1 C.C. 3 D.D. 2

Question 92. (THPT Nguyễn Quốc Trinh - Hà Nội 2025) Đồ thị hàm số $y=\dfrac{2x+1}{x-1}$ có phương trình đường tiệm cận ngang là

A.A. $x=1$ B.B. $y=1$ C.C. $y=2$ D.D. $x=2$

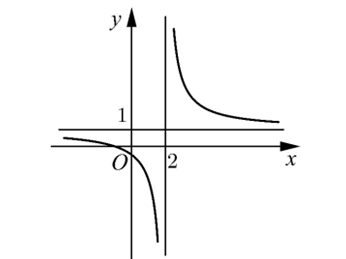
Question 93. (Sở Hải Phòng 2025) Hàm số $y=f(x)$ có đồ thị như hình dưới đây
Đồ thị hàm số đã cho có tiệm cận ngang là:

A.A. $y=2$ B.B. $x=2$ C.C. $y=1$ D.D. $x=1$

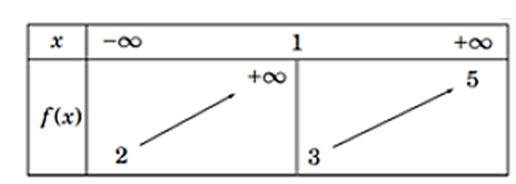
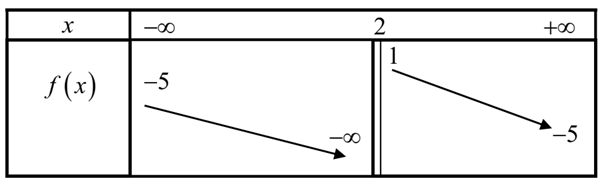
Question 94. (Chuyên Lam Sơn - Thanh Hóa 2025) Cho hàm số $y=f(x)$ có bảng biến thiên như sau
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là

A.A. 4 B.B. 2 C.C. 3 D.D. 1

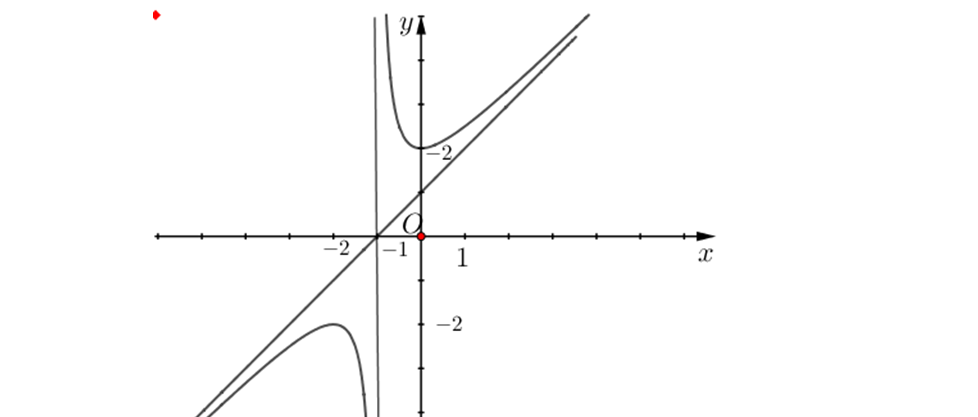
Question 95. (Cụm THPT Hoàn Kiếm - Hai Bà Trưng - Hà Nội 2025) Cho hàm số có đồ thị như hình vẽ bên:
Tiệm cận xiên của đồ thị hàm số là

A.A. $y=x+1$ B.B. $y=-x+1$ C.C. $y=-2x+1$ D.D. $y=2x+1$

Question 96. (Sở Gia Lai 2025) Phương trình đường tiệm cận đứng của đồ thị hàm số $y=\dfrac{2x+2}{x-1}$ là

A.A. $x=1$ B.B. $x=2$ C.C. $x=-1$ D.D. $x=-2$

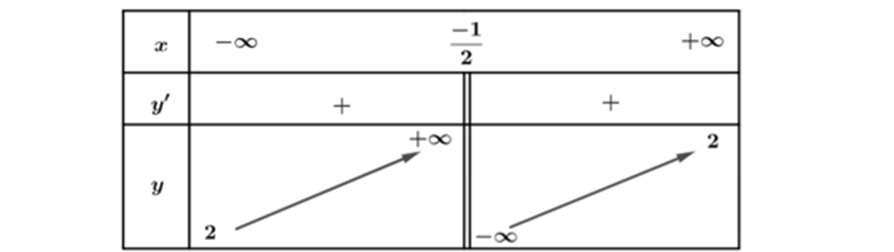
Question 97. (THPT Bắc Đông Quan - Thái Bình 2025) Cho hàm số $f(x)$ liên tục trên mỗi khoảng $(-\infty;-\dfrac{1}{2})$ và $(-\dfrac{1}{2};+\infty)$ và có bảng biến thiên như hình vẽ
Tiệm cận ngang của đồ thị hàm số là đường thẳng có phương trình

A.A. $x=2$ B.B. $y=-\dfrac{1}{2}$ C.C. $x=-\dfrac{1}{2}$ D.D. $y=2$

Question 98. (Sở Thái Bình 2025) Tiệm cận đứng của đồ thị hàm số $y=\dfrac{2x-1}{x+2}$ là đường thẳng có phương trình

A.A. $x=\dfrac{1}{2}$ B.B. $y=2$ C.C. $x=-2$ D.D. $y=-2$

Question 99. (Liên trường THPT Ninh Bình 2025) Tiệm cận đứng của đồ thị hàm số $y=\dfrac{3x+2}{x-2}$ là đường thẳng có phương trình

A.A. $x=-1$ B.B. $x=-2$ C.C. $x=2$ D.D. $x=3$

Question 100. Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số $y=\dfrac{x+1}{x^2-1}$ là

A.2 B.1 C.3 D.4

Question 101. Đồ thị hàm số $y=\dfrac{x+1}{x^2-2024x-2025}$ có bao nhiêu tiệm cận đứng?

A.3 B.1 C.2 D.0

Question 102. Tìm tất cả các tiệm cận đứng của đồ thị hàm số $y=\dfrac{x^2+2x-3}{x^2-4x+3}$.

A.$x=1$ B.$x=1$ và $x=3$ C.$x=3$ D.$y=1$

Question 103. Đồ thị hàm số $y=\dfrac{2x-3}{x^2+4x+4}$ có tiệm cận đứng $x=a$ và tiệm cận ngang $y=b$. Tính $S=a+2b$.

A.$S=-2$ B.$S=2$ C.$S=-4$ D.$S=4$

Question 104. Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số $y=\dfrac{2x^2-3x+1}{x^2-1}$ là

A.1 B.0 C.3 D.2

Question 105. Đồ thị hàm số $y=\dfrac{x-1}{x^2+2}$ có bao nhiêu đường tiệm cận ?

A.0 B.1 C.2 D.3

Question 106. Đồ thị hàm số $y=\dfrac{x+3}{x^3-3x}$ có bao nhiêu đường tiệm cận?

A.4 B.1 C.3 D.2

Question 107. Cho hàm số $y=\dfrac{x^2-1}{x(x^2-2x-3)}$. Số đường tiệm cận của đồ thị hàm số là bao nhiêu ?

A.3 B.2 C.1 D.4

Question 108. Đồ thị hàm số nào sau đây có ba đường tiệm cận ?

A.$y=\dfrac{x}{x^2-x+9}$ B.$y=\dfrac{1-2x}{1+x}$ C.$y=\dfrac{x+3}{5x-1}$ D.$y=\dfrac{1}{4-x^2}$

Question 109. Cho hàm số $y=\dfrac{x-9x^4}{(3x^2-3)^2}$. Khẳng định nào sau đây là khẳng định đúng?

A.Đồ thị hàm số có 2 tiệm cận đứng, có 1 tiệm cận ngang $y=-1$ B.Đồ thị hàm số có 2 tiệm cận đứng, có 1 tiệm cận ngang $y=-3$ C.Đồ thị hàm số có tiệm cận đứng, không có tiệm cận ngang D.Đồ thị hàm số không có tiệm cận đứng, có tiệm cận ngang

Question 110. Đồ thị hàm số $y=\dfrac{2x-1}{|x|+1}$ có bao nhiêu đường tiệm cận?

A.0 B.1 C.2 D.3

Question 111. Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số $y=\dfrac{x+1}{x^2-1}$ là

A.2 B.1 C.3 D.4

Question 112. Đồ thị hàm số $y=\dfrac{x+1}{x^2-2024x-2025}$ có bao nhiêu tiệm cận đứng?

A.3 B.1 C.2 D.0

Question 113. Tìm tất cả các tiệm cận đứng của đồ thị hàm số $y=\dfrac{x^2+2x-3}{x^2-4x+3}$

A.$x=1$ B.$x=1$ và $x=3$ C.$x=3$ D.$y=1$

Question 114. Đồ thị hàm số $y=\dfrac{2x-3}{x^2+4x+4}$ có tiệm cận đứng $x=a$ và tiệm cận ngang $y=b$. Tính $S=a+2b$.

A.$S=-2$ B.$S=2$ C.$S=-4$ D.$S=4$

Question 115. Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số $y=\dfrac{2x^2-3x+1}{x^2-1}$ là

A.1 B.0 C.3 D.2

Question 116. Đồ thị hàm số $y=\dfrac{x-1}{x^2+2}$ có bao nhiêu đường tiệm cận ?

A.0 B.1 C.2 D.3

Question 117. Đồ thị hàm số $y=\dfrac{x+3}{x^3-3x}$ có bao nhiêu đường tiệm cận?

A.4 B.1 C.3 D.2

Question 118. Cho hàm số $y=\dfrac{x^2-1}{x(x^2-2x-3)}$. Số đường tiệm cận của đồ thị hàm số là bao nhiêu ?

A.3 B.2 C.1 D.4

Question 119. Đồ thị hàm số nào sau đây có ba đường tiệm cận ?

A.$y=\dfrac{x}{x^2-x+9}$ B.$y=\dfrac{1-2x}{1+x}$ C.$y=\dfrac{x+3}{5x-1}$ D.$y=\dfrac{1}{4-x^2}$

Question 120. Cho hàm số $y=\dfrac{x-9x^4}{(3x^2-3)^2}$. Khẳng định nào sau đây là khẳng định đúng?

Question 121. Đồ thị hàm số $y=\dfrac{\sqrt{x^2+1}}{x-2}$ có tất cả bao nhiêu đường tiệm cận ?

A.1 B.3 C.2 D.0

Question 122. Số đường tiệm cận đứng của đồ thị hàm số $y=\dfrac{\sqrt{x+3}-2}{x^2-1}$ là bao nhiêu ?

A.0 B.1 C.3 D.2

Question 123. Tìm tất cả các đường tiệm cận ngang của đồ thị hàm số $y=\dfrac{x}{\sqrt{x^2+1}}$.

A.$y=-1$ B.$y=1$ C.$y=1, y=-1$ D.$y=0$

Question 124. Đồ thị hàm số $y=\dfrac{\sqrt{4-x^2}}{x^2-3x-4}$ có tất cả bao nhiêu đường tiệm cận ?

A.3 B.0 C.2 D.1

Question 125. Đồ thị hàm số $y=\dfrac{x}{\sqrt{x^2-4}}$ có tất cả bao nhiêu đường tiệm cận ?

A.4 B.5 C.3 D.6

Question 126. Cho hàm số $y=\dfrac{\sqrt{4-x^2}}{x^2-9}$. Khẳng định nào sau đây là \textbf{đúng} ?

A.A. Đồ thị hàm số có tiệm cận đứng là $x=\pm 3$ B.B. Đồ thị hàm số có 2 tiệm cận đứng và 1 tiệm cận ngang C.C. Đồ thị hàm số không có tiệm cận D.D. Đồ thị hàm số có 2 tiệm cận đứng và 2 tiệm cận ngang

Question 127. Số đường tiệm cận của đồ thị hàm số $y=\dfrac{\sqrt{x^2+x-2}}{x-1}$

A.1 B.4 C.3 D.2

Question 128. Số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số $y=\dfrac{\sqrt{x-2}+1}{x^2-3x+2}$ là

A.4 B.1 C.3 D.2

Question 129. Đồ thị hàm số $y=\dfrac{2x+\sqrt{x^2-x}}{3x+1}$ có tất cả bao nhiêu đường tiệm cận?

A.2 B.3 C.0 D.1

Question 130. Tổng số tiệm cận đứng và tiệm cận ngang của đồ thị hàm số $y=\dfrac{\sqrt{x(4x+6)}-2}{x+2}$ là?

A.1 B.3 C.2 D.4

Question 131. Gọi n, d lần lượt là số đường tiệm cận ngang và số tiệm cận đứng của đồ thị hàm số $y=\dfrac{\sqrt{1-x}}{(x-1)\sqrt{x}}$. Khẳng định nào sau đây là đúng?

A.$n=0, d=2$ B.$n=d=1$ C.$n=1, d=2$ D.$n=0, d=1$

Question 132. Đồ thị hàm số $y=\dfrac{\sqrt{4x^2+2x-1}+x}{x+1}$ có bao nhiêu đường tiệm cận?

A.1 B.0 C.2 D.3

Question 133. Hàm số $y=\dfrac{x+\sqrt{x^2+x+1}}{x^2+x}$ có bao nhiêu đường tiệm cận?

A.1 B.3 C.2 D.4

Question 134. Đồ thị hàm số $y=\dfrac{1-\sqrt{4-x^2}}{x^2-2x-3}$ có số đường tiệm cận đứng là $m$ và số đường tiệm cận ngang là $n$. Giá trị của $m+n$ là

A.1 B.2 C.3 D.0

Question 135. Đồ thị hàm số $y=\dfrac{5x-8}{\sqrt{x^2-3x}}$ có bao nhiêu đường tiệm cận?

A.2 B.4 C.1 D.3

Question 136. Tìm tất cả các tiệm cận đứng của đồ thị hàm số $y=\dfrac{2x-1-\sqrt{x^2+x+3}}{x^2-5x+6}$.

A.$x=3$ và $x=2$ B.$x=3$ C.$x=-3$ và $x=-2$ D.$x=-3$

Question 137. Đồ thị hàm số $f(x)=\dfrac{x+1}{\sqrt{x^2-1}}$ có tất cả bao nhiêu tiệm cận đứng và tiệm cận ngang?

A.4 B.3 C.1 D.2

Question 138. Cho hàm số $y=\dfrac{x^2+3x+2}{\sqrt{x^4-3x^2+2}}$. Đồ thị hàm số đã cho có bao nhiêu đường tiệm cận?

A.4 B.5 C.3 D.6

Question 139. Số đường tiệm cận của đồ thị hàm số $y=\dfrac{\sqrt{x-1}(\sqrt{x+1}-2)}{x^2-4x+3}$

A.3 B.1 C.4 D.2

Question 140. Số tiệm cận của đồ thị hàm số $y=\dfrac{\sqrt{x^2-1}}{|x|-1}$ là

A.4 B.1 C.3 D.2

Question 141. Cho hàm số $y=f(x)$ có bảng biến thiên như sau:
Số đường tiệm cận của đồ thị hàm số đã cho là

A.3 B.1 C.4 D.2

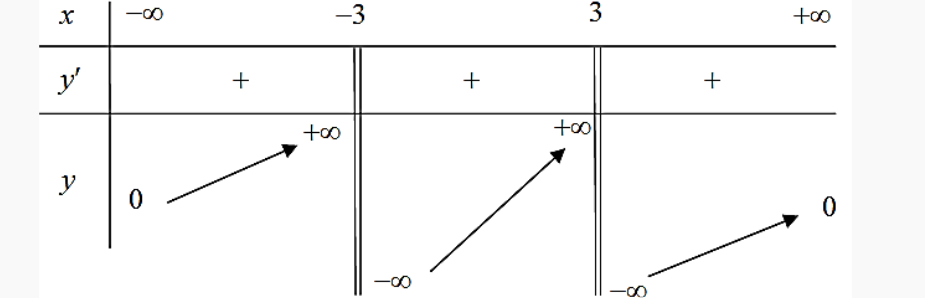
Question 142. Cho hàm số $y = f(x)$ xác định và có đạo hàm trên $\mathbb{R} \setminus \{\pm 1\}$. Hàm số có bảng biến thiên như hình vẽ dưới đây. Hỏi hàm số $y=f(x)$ có bao nhiêu tiệm cận?

A.1 B.4 C.3 D.2

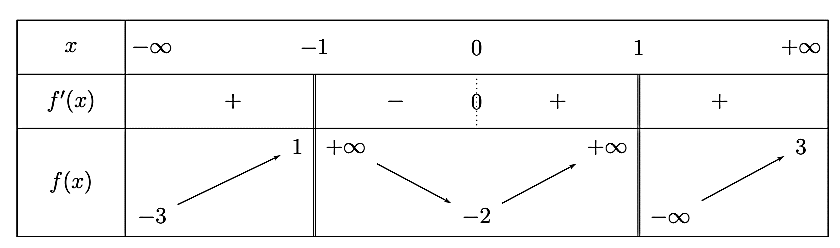
Question 143. Cho hàm số $y=f(x)$ có bảng biến thiên như hình vẽ. Hỏi đồ thị của hàm số đã cho có bao nhiêu đường tiệm cận?

A.1 B.3 C.C.2 D.D.4

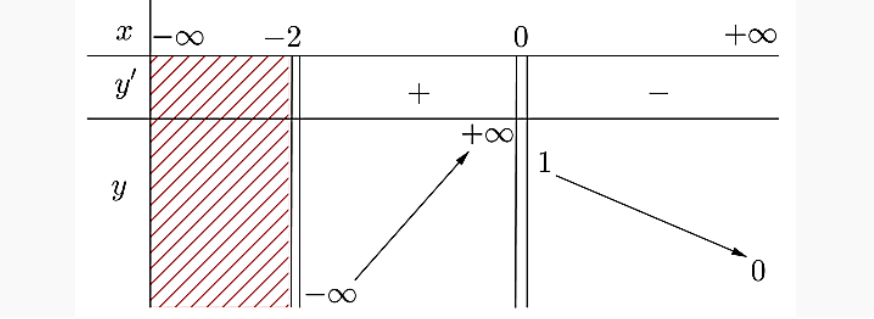
Question 144. Cho hàm số $y = f(x)$ có bảng biến thiên như sau:
Tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho bằng:

A.1 B.2 C.3 D.4

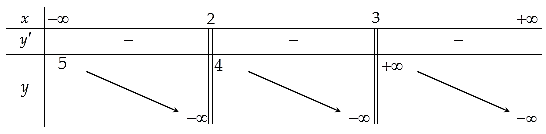
Question 145. Cho hàm số $y=f(x)$ có bảng biến thiên như hình vẽ
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho là

A.3 B.4 C.2 D.1

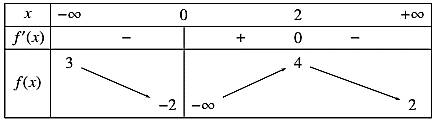
Question 146. Cho hàm số $y=f(x)$ có bảng biến thiên như sau:
Tổng số đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số đã cho bằng

A.1 B.2 C.3 D.4

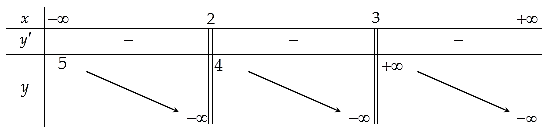
Question 147. Cho hàm số $y = f(x)$ có bảng biến như sau:
Số đường tiệm cận của đồ thị hàm số là

A.3 B.1 C.4 D.2

Question 148. Cho hàm số $y=f(x)$ có $\lim_{x \to -\infty} f(x) = -1$ và $\lim_{x \to +\infty} f(x)=-1$. Tìm phương trình đường tiệm cận ngang của đồ thị hàm số $y = 2-2026f(x)$.

A.$y=-2026$ B.$y=2028$ C.$y=2026$ D.$y=-2028$

Question 149. Cho đồ thị hàm số $y=f(x)=\dfrac{3x-1}{x-1}$. Khi đó đường thẳng nào sau đây là đường tiệm cận đứng của đồ thị hàm số $y=\dfrac{1}{f(x)-2}$?

A.$x=1$ B.$x=-2$ C.$x=-1$ D.$x=2$

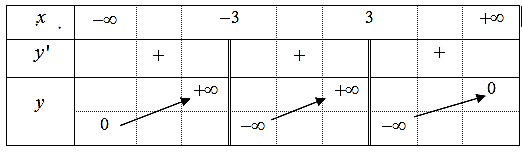
Question 150. Cho hàm số $y = f(x)$ có bảng biến thiên như hình bên. Số tiệm cận đứng của đồ thị hàm số $y=\dfrac{2030}{f(x)}$ là

A.1 B.2 C.3 D.4

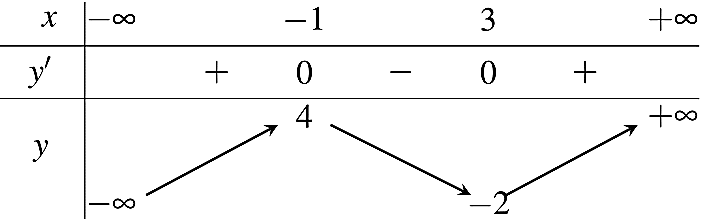
Question 151. Cho hàm số $y=f(x)$ xác định trên $\mathbb{R} \setminus \{-1;2\}$, liên tục trên các khoảng xác định của nó và có bảng biến thiên như sau:
Số đường tiệm cận của đồ thị hàm số $y = \dfrac{1}{f(x)-1}$

A.5 B.4 C.6 D.7

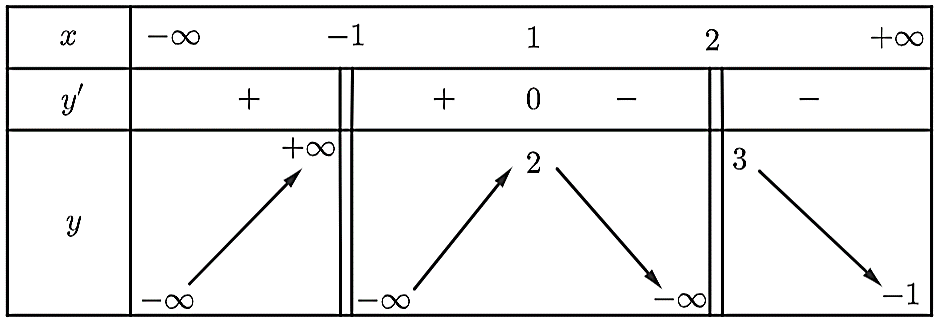
Question 152. Cho hàm số $f(x)$ xác định và liên tục trên $\mathbb{R} \setminus \{-1\}$ có bảng biến thiên như sau:
Hỏi đồ thị hàm số $y = \dfrac{1}{f(x)}$ có tất cả bao nhiêu đường tiệm cận đứng và tiệm cận ngang?

A.4 B.3 C.2 D.1

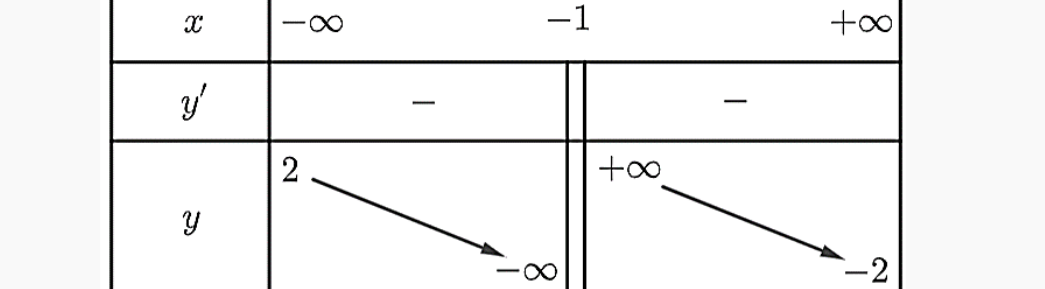
Question 153. Cho hàm số $y=f(x)$ liên tục trên $\mathbb{R} \setminus \{1\}$ và có bảng biến thiên như sau:
Đồ thị hàm số $y = \dfrac{1}{2f(x)-5}$ có bao nhiêu đường tiệm cận đứng ?

A.0 B.4 C.2 D.1

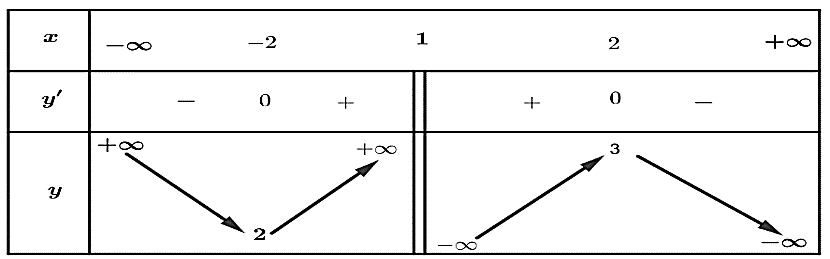
Question 154. Cho hàm số $y=f(x)$ có bảng biến thiên:
Đồ thị hàm số $y = \dfrac{1}{2f(x)-5}$ có tất cả bao nhiêu đường tiệm cận đứng?

A.5 B.3 C.6 D.4

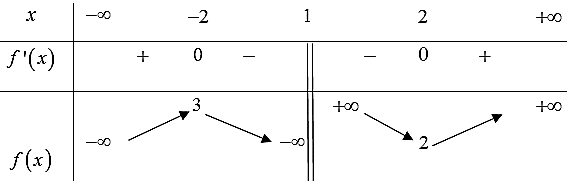
Question 155. Cho hàm số $y=f(x)$ có bảng biến thiên như hình dưới đây.
Tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số $y=\dfrac{1}{2f(x)-1}$ là

A.0 B.1 C.2 D.3

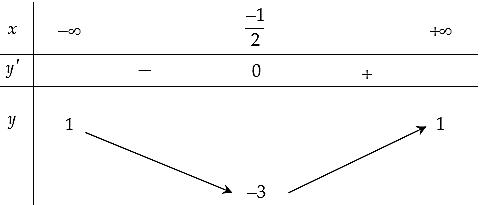
Question 156. Cho hàm số $y=f(x)$ liên tục trên $\mathbb{R} \setminus \{1\}$ và có bảng biến thiên như sau:
Đồ thị $y=\dfrac{1}{2f(x)+3}$ có bao nhiêu đường tiệm cận đứng?

A.2 B.0 C.1 D.3

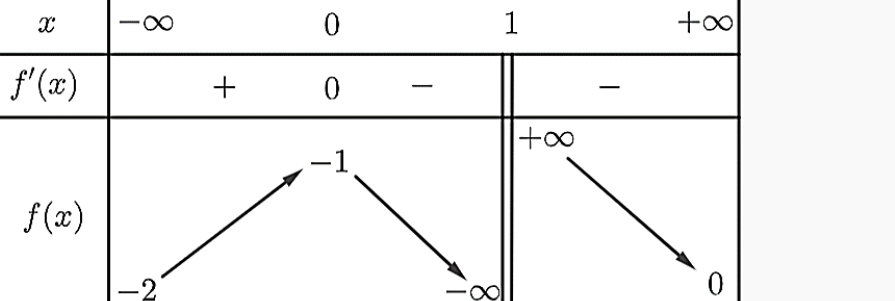
Question 157. Cho hàm số $y=f(x)$ xác định và có đạo hàm trên $\mathbb{R} \setminus \{\pm 2\}$. Hàm số $f(x)$ có bảng biến thiên như hình vẽ dưới đây
Tính tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số $y=\dfrac{1}{2f(x)+6}$.

A.6 B.5 C.3 D.4

Question 158. Tìm m để tiệm cận đứng của đồ thị hàm số $y = \dfrac{x+3}{x+m-1}$ đi qua điểm $A(5;2)$.

A.$m=-4$ B.$m=-1$ C.$m=6$ D.$m=4$

Question 159. Tìm m để đồ thị hàm số $y = \dfrac{(m+1)x-5m}{2x-m}$ có tiệm cận ngang là $y=1$.

A.$m=2$ B.$m=-\dfrac{5}{2}$ C.$m=0$ D.$m=1$

Question 160. Cho hàm số $y = \dfrac{ax+1}{bx-2}$. Tìm $S=a+b$ để đồ thị hàm số có $x=1$ là tiệm cận đứng và $y=\dfrac{1}{2}$ là tiệm cận ngang.

A.$S=-3$ B.$S=3$ C.$S=1$ D.$S=8$

Question 161. Tìm tham số thực m để đồ thị hàm số $y = \dfrac{mx+3}{x-m}$ có tiệm cận đứng là đường $x=1$, tiệm cận ngang là đường $y=1$.

A.$m=1$ B.$m=2$ C.$m=-1$ D.$m=3$

Question 162. Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số $y = \dfrac{4x-5}{x-m}$ có tiệm cận đứng nằm bên phải trục $Oy$.

A.$m=0$ B.$m<0$ C.$m>0$ D.$m \ne 0$

Question 163. Xác định hàm số $y = \dfrac{ax+b}{cx+d}$; biết rằng đồ thị hàm số cắt trục tung tại điểm $M(0;1)$ và đồ thị có giao điểm hai đường tiệm cận là $I(1;-1)$?

A.$y = \dfrac{x+1}{x-1}$ B.$y = \dfrac{x-2}{-x-2}$ C.$y = \dfrac{2x-1}{x-1}$ D.$y = \dfrac{x+1}{1-x}$

Question 164. Cho hàm số $y = \dfrac{3x+1}{x-1}$ có đồ thị (C) và M là điểm bất kì thuộc (C). Gọi $d_1, d_2$ lần lượt là khoảng cách từ điểm M đến đường tiệm cận đứng và đường tiệm cận ngang. Tính tích $d_1d_2$.

A.$d_1d_2 = 2$ B.$d_1d_2 = 3$ C.$d_1d_2=4$ D.$d_1d_2 = 6$

Question 165. Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số $y = \dfrac{x-4}{x^2-mx+4}$ có hai đường tiệm cận đứng ?

A.$m \in (-\infty;-4] \cup [4;+\infty)$ B.$m \ne 5$ C.$m \in (-\infty;-4) \cup (4;+\infty) \setminus \{5\}$ D.$m \in (-\infty;-4) \cup (4;+\infty)$

Question 166. Cho hàm số $y = \dfrac{2x^2-3x+m}{x-m}$ có đồ thị (C). Tìm tham số m để (C) không có tiệm cận đứng?

A.$m=0$ B.$m=1$ C.$m=2$ D.$m=0$ hoặc $m=1$

Question 167. Cho hàm số $y = \dfrac{x+3}{x^2+4x+m}$. Tìm tham số m để đồ thị hàm số có ba tiệm cận?

A.$m>4$ và $m \ne 3$ B.$m<4$ C.$m<4$ và $m \ne 3$ D.$m \in \mathbb{R}$

Question 168. Cho hàm số $y=\dfrac{mx+1}{x+3n+1}$. Đồ thị hàm số nhận trục hoành và trục tung làm tiệm cận ngang và tiệm cận đứng. Tính $m+n$.

A.$m+n=-\dfrac{1}{3}$ B.$m+n=\dfrac{1}{3}$ C.$m+n=\dfrac{2}{3}$ D.$m+n=0$

Question 169. Biết đồ thị hàm số $y=\dfrac{(2m-n)x^2+mx+1}{x^2+mx+n-6}$ nhận trục hoành và trục tung làm hai tiệm cận. Tính $m+n$.

A.$m+n=6$ B.$m+n=-6$ C.$m+n=8$ D.$m+n=9$

Question 170. Có bao nhiêu giá trị của m để hai đường tiệm cận của đồ thị hàm số $f(x)=\dfrac{2x+3}{x-m}$ tạo với hai trục toạ độ một hình chữ nhật có diện tích bằng 2024.

A.4 B.1 C.2 D.3

Question 171. Có bao nhiêu giá trị nguyên $m \in [-10;10]$ sao cho đồ thị hàm số $y = \dfrac{x-1}{2x^2+6x-m-3}$ có hai đường tiệm cận đứng?

A.19 B.15 C.17 D.18

Question 172. Tổng các giá trị của tham số m để đồ thị của hàm số $y=\dfrac{x-1}{x^2+2(m-1)x+m^2-2}$ có đúng một tiệm cận đứng.

A.$-\dfrac{1}{2}$ B.2 C.-3 D.$\dfrac{3}{2}$

Question 173. Cho hàm số $y=\dfrac{x-3}{x^3-3mx^2+(2m^2+1)x-m}$. Có bao nhiêu giá trị nguyên thuộc đoạn $[-6;6]$ của tham số m để đồ thị hàm số có bốn đường tiệm cận?

A.12 B.9 C.8 D.11

Question 174. Có bao nhiêu giá trị nguyên của m để tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số $y=\dfrac{\sqrt{mx^2+3mx+4}}{x+2}$ bằng 3?

A.4 B.1 C.2 D.3

Question 175. Tìm tất cả các giá trị thực của tham số m sao cho đồ thị của hàm số $y=\dfrac{x-1}{x^3-3x^2-m}$ có đúng một tiệm cận đứng.

A.$\begin{cases} m>0 \\ m<-4 \end{cases}$ B.$\begin{cases} m \ge 0 \\ m \le -4 \end{cases}$ C.$\begin{cases} m>0 \\ m \le -4 \end{cases}$ D.$m \in \mathbb{R}$

Question 176. Cho hàm số $y=\dfrac{3x-1}{x+2}$ (C) và đường thẳng $5x-12y+7=0 (\triangle)$. Khoảng cách từ giao điểm của hai đường tiệm cận của đồ thị (C) đến đường thẳng $(\triangle)$ bằng:

A.$\dfrac{46}{13}$ B.$\dfrac{37}{13}$ C.$\dfrac{41}{3}$ D.3

Question 177. Cho hàm số $y=\dfrac{x^2+2x+4}{x+2}$ có đồ thị (C). Tích khoảng cách từ M bất kỳ trên (C) đến hai đường tiệm cận của (C) bằng:

A.$2\sqrt{2}$ B.2 C.$\sqrt{2}$ D.1

Question 178. Cho hàm số $y=\dfrac{mx-1}{x-n}$, trong đó $m, n$ là tham số. Biết giao điểm của hai đường tiệm cận của đồ thị hàm số nằm trên đường thẳng $x-2y+3=0$ và đồ thị hàm số đi qua điểm $A(0,1)$. Giá trị của $m+n$ là

A.$m+n=-3$ B.$m+n=-1$ C.$m+n=3$ D.$m+n=1$

Question 179. Cho hàm số $y=\dfrac{x-3}{x+1}$ có đồ thị là (C). Gọi I là giao điểm của hai đường tiệm cận của (C). Tìm tọa độ điểm M trên (C) sao cho độ dài đoạn IM ngắn nhất.

A.$M_1(1;1)$ và $M_2(-3;0)$ B.$M_1(1;-1)$ và $M_2(-3;3)$ C.$M_1(1;-1)$ và $M_2(-3;2)$ D.$M_1(1;-2)$ và $M_2(-3;-3)$

Question 180. Gọi $M(a;b), b>0$ là điểm thuộc đồ thị hàm số $y=\dfrac{2x-10}{x-3}$ sao cho tổng khoảng cách từ M đến hai đường tiệm cận của đồ thị hàm số đó đạt giá trị nhỏ nhất. Khi đó hiệu $a-b$ bằng

A.-3 B.-5 C.5 D.3

Question 181. Cho hàm số $y=\dfrac{2x-3}{x-2}$ (C). Gọi M là điểm bất kì trên (C), d là tổng khoảng cách từ M đến hai đường tiệm cận của đồ thị (C). Giá trị nhỏ nhất của d.

A.10 B.2 C.5 D.6

Question 182. Cho hàm số $y=\dfrac{x+1}{x-1}$ có đồ thị (C) và A là điểm thuộc (C). Tính giá trị nhỏ nhất của tổng các khoảng cách từ A đến các đường tiệm cận của (C).

A.$2\sqrt{3}$ B.2 C.3 D.$2\sqrt{2}$

Question 183. Cho đồ thị (C): $y=\dfrac{2x+1}{x-1}$. Gọi M là điểm bất kì thuộc đồ thị (C). Tiếp tuyến của đồ thị (C) tại M cắt hai đường tiệm cận của (C) tại hai điểm P và Q. Gọi G là trọng tâm tam giác IPQ (với I là giao điểm hai đường tiệm cận của (C)). Diện tích tam giác GPQ là

A.2 B.4 C.$\dfrac{2}{3}$ D.1

Question 184. Cho hàm số $y=\dfrac{2x-1}{x+1}$ có đồ thị là (C). Gọi I là giao điểm của hai đường tiệm cận, $M(x_0,y_0), x_0>0$ là một điểm trên (C) sao cho tiếp tuyến với (C) tại M cắt hai đường tiệm cận lần lượt tại A, B thỏa mãn $AI^2+IB^2=40$. Tính tích $x_0y_0$.

A.$\dfrac{1}{2}$ B.2 C.1 D.$\dfrac{15}{4}$

Question 185. Tìm m để tiệm cận đứng của đồ thị hàm số $y = \dfrac{x+3}{x+m-1}$ đi qua điểm $A(5;2)$.

A.$m=-4$ B.$m=-1$ C.$m=6$ D.$m=4$

Question 186. Tìm m để đồ thị hàm số $y = \dfrac{(m+1)x-5m}{2x-m}$ có tiệm cận ngang là $y=1$.

A.$m=2$ B.$m=-\dfrac{5}{2}$ C.$m=0$ D.$m=1$

Question 187. Cho hàm số $y = \dfrac{ax+1}{bx-2}$. Tìm $S=a+b$ để đồ thị hàm số có $x=1$ là tiệm cận đứng và $y=\dfrac{1}{2}$ là tiệm cận ngang.

A.$S=-3$ B.$S=3$ C.$S=1$ D.$S=8$

Question 188. Tìm tham số thực m để đồ thị hàm số $y = \dfrac{mx+3}{x-m}$ có tiệm cận đứng là đường $x=1$, tiệm cận ngang là đường $y=1$.

A.$m=1$ B.$m=2$ C.$m=-1$ D.$m=3$

Question 189. Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số $y = \dfrac{4x-5}{x-m}$ có tiệm cận đứng nằm bên phải trục $Oy$.

A.$m=0$ B.$m<0$ C.$m>0$ D.$m \ne 0$

Question 190. Xác định hàm số $y = \dfrac{ax+b}{cx+d}$; biết rằng đồ thị hàm số cắt trục tung tại điểm $M(0;1)$ và đồ thị có giao điểm hai đường tiệm cận là $I(1;-1)$?

A.$y = \dfrac{x+1}{x-1}$ B.$y = \dfrac{x-2}{-x-2}$ C.$y = \dfrac{2x-1}{x-1}$ D.$y = \dfrac{x+1}{1-x}$

Question 191. Cho hàm số $y = \dfrac{3x+1}{x-1}$ có đồ thị (C) và M là điểm bất kì thuộc (C). Gọi $d_1, d_2$ lần lượt là khoảng cách từ điểm M đến đường tiệm cận đứng và đường tiệm cận ngang. Tính tích $d_1d_2$.

A.$d_1d_2 = 2$ B.$d_1d_2 = 3$ C.$d_1d_2=4$ D.$d_1d_2 = 6$

Question 192. Tìm tất cả các giá trị thực của tham số m để đồ thị hàm số $y = \dfrac{x-4}{x^2-mx+4}$ có hai đường tiệm cận đứng ?

A.$m \in (-\infty;-4] \cup [4;+\infty)$ B.$m \ne 5$ C.$m \in (-\infty;-4) \cup (4;+\infty) \setminus \{5\}$ D.$m \in (-\infty;-4) \cup (4;+\infty)$

Question 193. Cho hàm số $y = \dfrac{2x^2-3x+m}{x-m}$ có đồ thị (C). Tìm tham số m để (C) không có tiệm cận đứng?

A.$m=0$ B.$m=1$ C.$m=2$ D.$m=0$ hoặc $m=1$

Question 194. Cho hàm số $y = \dfrac{x+3}{x^2+4x+m}$. Tìm tham số m để đồ thị hàm số có ba tiệm cận?

A.$m>4$ và $m \ne 3$ B.$m<4$ C.$m<4$ và $m \ne 3$ D.$m \in \mathbb{R}$

Question 195. Cho hàm số $y=\dfrac{mx+1}{x+3n+1}$. Đồ thị hàm số nhận trục hoành và trục tung làm tiệm cận ngang và tiệm cận đứng. Tính $m+n$.

A.$m+n=-\dfrac{1}{3}$ B.$m+n=\dfrac{1}{3}$ C.$m+n=\dfrac{2}{3}$ D.$m+n=0$

Question 196. Biết đồ thị hàm số $y=\dfrac{(2m-n)x^2+mx+1}{x^2+mx+n-6}$ nhận trục hoành và trục tung làm hai tiệm cận. Tính $m+n$.

A.$m+n=6$ B.$m+n=-6$ C.$m+n=8$ D.$m+n=9$

Question 197. Có bao nhiêu giá trị của m để hai đường tiệm cận của đồ thị hàm số $f(x)=\dfrac{2x+3}{x-m}$ tạo với hai trục toạ độ một hình chữ nhật có diện tích bằng 2024.

A.4 B.1 C.2 D.3

Question 198. Có bao nhiêu giá trị nguyên $m \in [-10;10]$ sao cho đồ thị hàm số $y = \dfrac{x-1}{2x^2+6x-m-3}$ có hai đường tiệm cận đứng?

A.19 B.15 C.17 D.18

Question 199. Tổng các giá trị của tham số m để đồ thị của hàm số $y=\dfrac{x-1}{x^2+2(m-1)x+m^2-2}$ có đúng một tiệm cận đứng.

A.$-\dfrac{1}{2}$ B.2 C.-3 D.$\dfrac{3}{2}$

Question 200. Cho hàm số $y=\dfrac{x-3}{x^3-3mx^2+(2m^2+1)x-m}$. Có bao nhiêu giá trị nguyên thuộc đoạn $[-6;6]$ của tham số m để đồ thị hàm số có bốn đường tiệm cận?

A.12 B.9 C.8 D.11

Question 201. Có bao nhiêu giá trị nguyên của m để tổng số tiệm cận ngang và tiệm cận đứng của đồ thị hàm số $y=\dfrac{\sqrt{mx^2+3mx+4}}{x+2}$ bằng 3?

A.4 B.1 C.2 D.3

Question 202. Tìm tất cả các giá trị thực của tham số m sao cho đồ thị của hàm số $y=\dfrac{x-1}{x^3-3x^2-m}$ có đúng một tiệm cận đứng.

A.$\begin{cases} m>0 \\ m<-4 \end{cases}$ B.$\begin{cases} m \ge 0 \\ m \le -4 \end{cases}$ C.$\begin{cases} m>0 \\ m \le -4 \end{cases}$ D.$m \in \mathbb{R}$

Question 203. Cho hàm số $y=\dfrac{3x-1}{x+2}$ (C) và đường thẳng $5x-12y+7=0 (\triangle)$. Khoảng cách từ giao điểm của hai đường tiệm cận của đồ thị (C) đến đường thẳng $(\triangle)$ bằng:

A.$\dfrac{46}{13}$ B.$\dfrac{37}{13}$ C.$\dfrac{41}{3}$ D.3

Question 204. Cho hàm số $y=\dfrac{x^2+2x+4}{x+2}$ có đồ thị (C). Tích khoảng cách từ M bất kỳ trên (C) đến hai đường tiệm cận của (C) bằng:

A.$2\sqrt{2}$ B.2 C.$\sqrt{2}$ D.1

Question 205. Cho hàm số $y=\dfrac{mx-1}{x-n}$, trong đó $m, n$ là tham số. Biết giao điểm của hai đường tiệm cận của đồ thị hàm số nằm trên đường thẳng $x-2y+3=0$ và đồ thị hàm số đi qua điểm $A(0,1)$. Giá trị của $m+n$ là

A.$m+n=-3$ B.$m+n=-1$ C.$m+n=3$ D.$m+n=1$

Question 206. Cho hàm số $y=\dfrac{x-3}{x+1}$ có đồ thị là (C). Gọi I là giao điểm của hai đường tiệm cận của (C). Tìm tọa độ điểm M trên (C) sao cho độ dài đoạn IM ngắn nhất.

A.$M_1(1;1)$ và $M_2(-3;0)$ B.$M_1(1;-1)$ và $M_2(-3;3)$ C.$M_1(1;-1)$ và $M_2(-3;2)$ D.$M_1(1;-2)$ và $M_2(-3;-3)$

Question 207. Gọi $M(a;b), b>0$ là điểm thuộc đồ thị hàm số $y=\dfrac{2x-10}{x-3}$ sao cho tổng khoảng cách từ M đến hai đường tiệm cận của đồ thị hàm số đó đạt giá trị nhỏ nhất. Khi đó hiệu $a-b$ bằng

A.-3 B.-5 C.5 D.3

Question 208. Cho hàm số $y=\dfrac{2x-3}{x-2}$ (C). Gọi M là điểm bất kì trên (C), d là tổng khoảng cách từ M đến hai đường tiệm cận của đồ thị (C). Giá trị nhỏ nhất của d.

A.10 B.2 C.5 D.6

Question 209. Cho hàm số $y=\dfrac{x+1}{x-1}$ có đồ thị (C) và A là điểm thuộc (C). Tính giá trị nhỏ nhất của tổng các khoảng cách từ A đến các đường tiệm cận của (C).

A.$2\sqrt{3}$ B.2 C.3 D.$2\sqrt{2}$

Question 210. Cho đồ thị (C): $y=\dfrac{2x+1}{x-1}$. Gọi M là điểm bất kì thuộc đồ thị (C). Tiếp tuyến của đồ thị (C) tại M cắt hai đường tiệm cận của (C) tại hai điểm P và Q. Gọi G là trọng tâm tam giác IPQ (với I là giao điểm hai đường tiệm cận của (C)). Diện tích tam giác GPQ là

A.2 B.4 C.$\dfrac{2}{3}$ D.1

Question 211. Cho hàm số $y=\dfrac{2x-1}{x+1}$ có đồ thị là (C). Gọi I là giao điểm của hai đường tiệm cận, $M(x_0,y_0), x_0>0$ là một điểm trên (C) sao cho tiếp tuyến với (C) tại M cắt hai đường tiệm cận lần lượt tại A, B thỏa mãn $AI^2+IB^2=40$. Tính tích $x_0y_0$.

A.$\dfrac{1}{2}$ B.2 C.1 D.$\dfrac{15}{4}$

📘 BÀI TIỆM CẬN

📘 BÀI TẬP TRẮC NGHIỆM

📋 Danh sách slide