LỚP TOÁN THẦY BÌNH
--:--:--

📘 KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ

Môn Toán - Lớp 12

📘 PHẦN ĐÚNG SAI

Question 1. (Cụm trường THPT Bắc Ninh 2025) Cho hàm số bậc ba $y = f(x) = ax^3+bx^2+cx+d$ có đồ thị là đường cong như hình vẽ bên.

a) a) Trong các số a,b,c,d có ba giá trị dương
b) b) Hàm số đạt giá trị lớn nhất trên (-2;1) bằng 3
c) c) Tâm đối xứng của đồ thị hàm số có hoành độ bằng 1
d) d) Phương trình $f(f(x)) = \dfrac{5}{2}$ có sáu nghiệm phân biệt

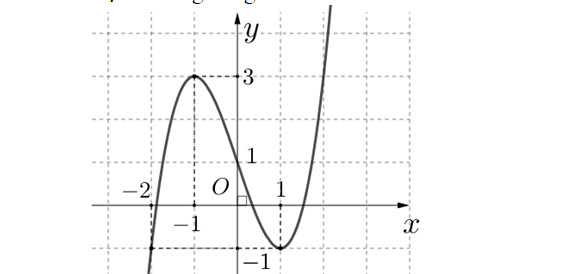
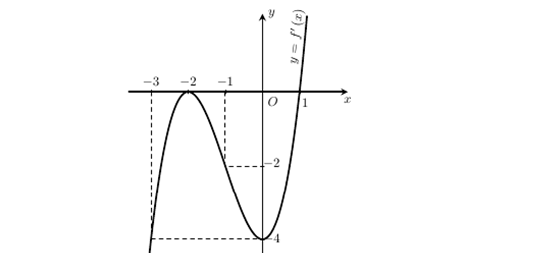
Question 2. (THPT Cẩm Xuyên - Hà Tĩnh 2025) Cho hàm số $f(x)$. Hàm số $y=f'(x)$ có đồ thị như hình vẽ.

a) a) $f(-1)>f(-3)$
b) b) Hàm số $f(x)$ đạt cực tiểu tại $x=-1$ và $x=4$
c) c) Hàm số $y=f(2-x)$ nghịch biến trên khoảng (1;3)
d) d) Trên đoạn [2024;2025] hàm số $g(x)=f(2-x)$ đạt giá trị nhỏ nhất tại $x=2024$

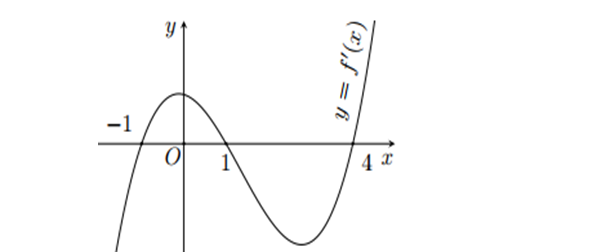
Question 3. (Chuyên KHTN Hà Nội 2025) Cho hàm số $y=f(x)$ có bảng biến thiên như hình vẽ

a) a) Hàm số đã cho có hai điểm cực đại
b) b) Giá trị nhỏ nhất của hàm số $y=f(\sqrt{x-3}+1)$ trên nửa khoảng $[3;+\infty)$ là 1
c) c) Phương trình $f(x)+x^2-6x=0$ có đúng hai nghiệm phân biệt lớn hơn 1
d) d) Có đúng 7 số nguyên m để phương trình $f(\sqrt{x-3}+1)+m(x+2-4\sqrt{x-3})=10$ có hai nghiệm

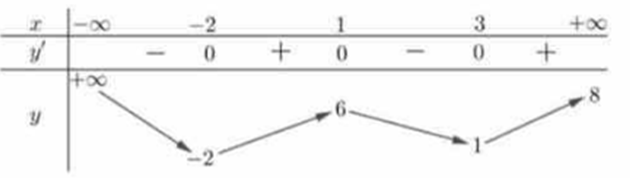
Question 4. (Chuyên Thái Bình 2025) Cho hàm số $y=f(x) = ax^3+bx^2+cx+d$ có bảng biến thiên như hình vẽ
Các khẳng định sau đúng hay sai?

a) a) Hàm số $y=f(x)$ có hai điểm cực trị
b) b) Hàm số $y=f(x)$ có giá trị lớn nhất bằng 2, giá trị nhỏ nhất bằng -2
c) c) Hàm số $g(x)=3-2f(x)$ nghịch biến trên (0;2)
d) d) Đồ thị hàm số $y=f(x)$ đi qua điểm A(-1;-2)

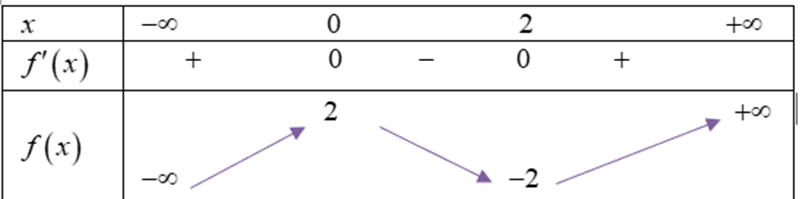
Question 5. (Cụm trường Nghệ An 2025) Cho hàm số bậc ba $y=f(x)$ có đồ thị là đường cong như hình vẽ.

a) a) Hàm số $y=f(x)$ có hai điểm cực trị
b) b) Giá trị nhỏ nhất của hàm số $y=f(x)$ trên đoạn [0;3] bằng -4
c) c) Hàm số $y=f(x)$ nghịch biến trên khoảng $(1;+\infty)$
d) d) Đồ thị hàm số $y=\dfrac{1}{f(x)}$ có đúng hai đường tiệm cận đứng

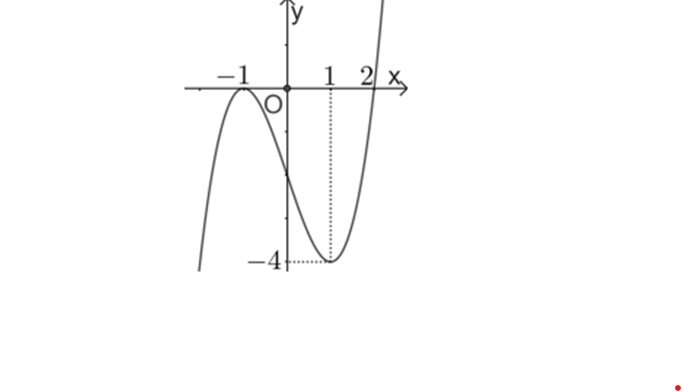
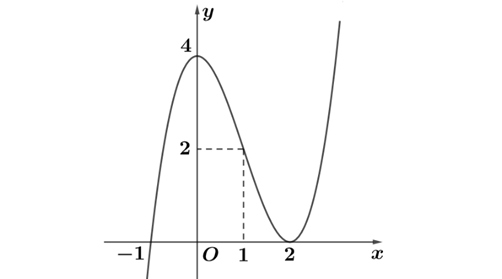
Question 6. (Cụm trường Nguyễn Hiền - Lê Hồng Phong - Quảng Nam 2025) Cho hàm số $y=-x^3+3x^2+4$ có đồ thị (C). Xét tính đúng sai của các mệnh đề sau:

a) a) Tập xác định của hàm số là $D=\mathbb{R}$ và $y'=-3x^2+6x$
b) b) Hàm số đồng biến trên khoảng (0;2)
c) c) Đồ thị (C) có hai điểm cực trị và phương trình đường thẳng đi qua 2 điểm cực trị là $2x+y-4=0$
d) d) Diện tích của tam giác OAB bằng 4, với O là gốc tọa độ và A, B là các điểm cực trị của (C)

Question 7. (THPT Anh Sơn 3 - Nghệ An 2025) Cho hàm số $y=f(x)$ có đạo hàm liên tục trên $\mathbb{R}$ và có đồ thị của hàm số $y=f'(x)$ như hình vẽ.

a) a) Hàm số $y=f(x)$ đồng biến trên khoảng $(-\infty;-2)$
b) b) Hàm số $y=f(x)$ có hai điểm cực trị
c) c) Trên đoạn [-2;1], hàm số $y=f(x)$ đạt giá trị nhỏ nhất tại $x=1$
d) d) Hàm số $g(x)=f(x^2-2)$ đồng biến trên các khoảng $(-\infty;-\sqrt{3})$ và $(0;\sqrt{3})$

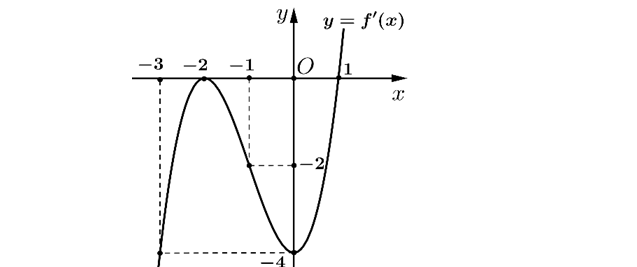
Question 8. (Sở Quảng Bình 2025) Cho hàm số $y=f(x)=x^3-3x^2+4$.

a) a) Hàm số $y=f(x)$ nghịch biến trên khoảng (0;2)
b) b) Giới hạn $\lim_{x\to+\infty} f(x)=+\infty$
c) c) Gọi A, B lần lượt là hai điểm cực trị của đồ thị hàm số $y=f(x)$. Khi đó độ dài AB bằng $\sqrt{5}$
d) d) Đồ thị hàm số $y=\dfrac{x+1}{f(x)}$ có đúng hai đường tiệm cận đứng

Question 9. (Sở Đà Nẵng 2025) Cho hàm số $f(x)=-2x^4+4x^2+1$ có đồ thị (C).

a) a) $\lim_{x\to-\infty} f(x)=-\infty$
b) b) Đạo hàm của hàm số đã cho là $f'(x)=-8x^3+8x+1$
c) c) Tập nghiệm của phương trình $f'(x)=0$ là $S=\{-1;0;1\}$
d) d) Giá trị lớn nhất của $f(x)$ là 1

Question 10. (Sở Thái Nguyên 2025) Cho hàm số $y=f(x)=x^3+bx^2+cx+2$ đạt cực trị bằng 0 tại $x=1$ (với b và c là hằng số)

a) a. Giá trị của $b+c$ bằng -3
b) b. Hàm số $y=f(x)$ đạt cực trị tại $x=-1$
c) c) Giá trị cực đại của hàm số đã cho bằng 0
d) d) Hàm số $y=f(x)$ đồng biến trên (-1;0)

Question 11. (THPT Hoằng Hóa 2-Thanh Hóa 2025) Cho hàm số $y=f(x)$ xác định và liên tục trên $\mathbb{R}$ có đồ thị như hình vẽ Các mệnh đề sau đây đúng hay sai?

a) a) Hàm số nghịch biến trên khoảng (-1;1)
b) b) Hàm số có $f'(x)>0 \ \forall x \in (-\infty;-1) \cup (1;+\infty)$
c) c) Hàm số $g(x)=f(x)+1$ nghịch biến trên khoàng (0;2)
d) d) Hàm số $y=f(|x|)$ đồng biến trên (-1;0) và $(1;+\infty)$

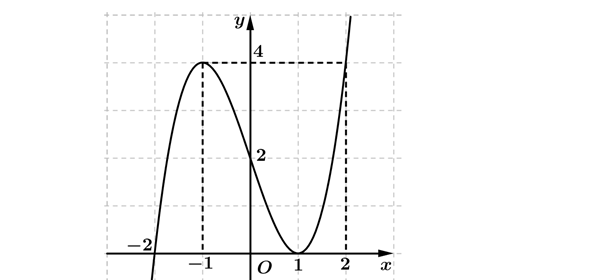
Question 12. (Đề thi vào ĐHSPHN 2025) Cho hàm số $y=f(x)$ liên tục trên $\mathbb{R}$, đạo hàm $f'(x)$ có đồ thị như hình sau:

a) a) Phương trình $f'(x)=0$ có 2 nghiệm phân biệt
b) b) Hàm số $y=f(x)$ nghịch biến trên (-1;1)
c) c) Hàm số $y=f(x)$ có điểm cực đại $x=-3$
d) d) Nếu $g(x)=f(1-x^2)$ thì $g(2025) < g(2026)$

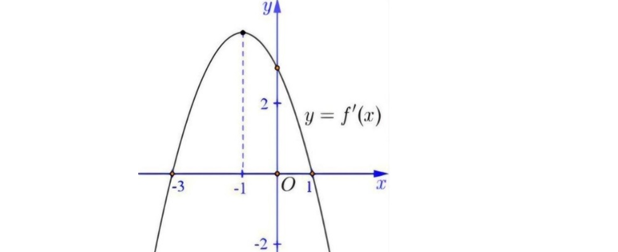
Question 13. (THPT Triệu Quang Phục - Hưng Yên 2025) Cho hàm số $y=f(x)$ có đạo hàm trên $\mathbb{R}$ và $f'(x)$ là hàm số bậc ba có đồ thị là đường cong trong hình vẽ bên dưới.

a) a) Hàm số $y=f(x)$ đồng biến trên khoảng $(-\infty;-2)$
b) b) Hàm số $y=f(x)$ có hai cực trị
c) c) $\underset{[-2;1]}{\text{Max}} f(x) = f(-2)$
d) d) Đồ thị hàm số $g(x)=\dfrac{x+2}{f'(x)}$ có tất cả 2 đường tiệm cận

Question 14. (THPT Triệu Quang Phục - Hưng Yên 2025) Cho hàm số $y=f(x)$ liên tục trên $\mathbb{R}$ và có bảng biến thiên như hình vẽ, m là số thực tùy ý Xét tính đúng, sai của các mệnh đề sau:

a) a) Giá trị lớn nhất của hàm số $y=f(x)$ trên [-1;3] bằng 2022 đạt tại $x=3$
b) b) Hàm số $y=f(x-2024)$ đồng biến trên (-2025;-2021)
c) c) Đồ thị hàm số $y=f(x)-2$ có tọa độ điểm cực tiểu là (-1;-2)
d) d) Bất phương trình $f(x) \ge a$ (tham số a) có nghiệm trên đoạn [-1;3] khi $a \le 2022$

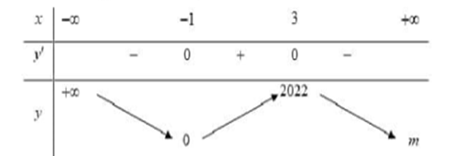
Question 15. (Sở Bắc Ninh 2025) Cho hàm số bậc ba $y=f(x)$ có bảng biến thiên như hình dưới đây

a) a) Hàm số $y=f(x)$ có 2 điểm cực trị
b) b) Hàm số $y=f(x)$ đồng biến trên $(-3;5)$
c) c) Đồ thị hàm số $g(x) = \dfrac{x-4}{f(x)-5}$ có 3 đường tiệm cận
d) d) Giá trị lớn nhất của hàm số $g(x)=f(4x-x^2)+\dfrac{1}{3}x^3-3x^2+8x+\dfrac{1}{3}$ trên đoạn [1;3] bằng 12

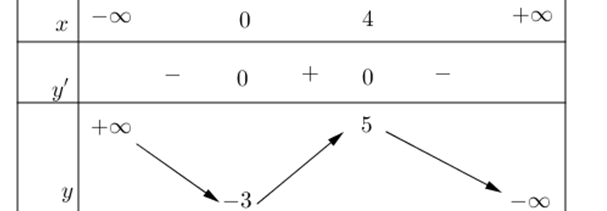
Question 16. (Sở Hậu Giang 2025) Cho hàm số bậc ba $y=f(x)$ có đồ thị như hình vẽ:

a) a. Hàm số $f(x)$ nghịch biến trên khoảng (-1;1)
b) b) Hàm số $f(x)$ có hai điểm cực trị
c) c) Trên đoạn [-2;2], hàm số $f(x)$ đạt giá trị lớn nhất bằng 2
d) d) $f(x)=x^3-3x+1$

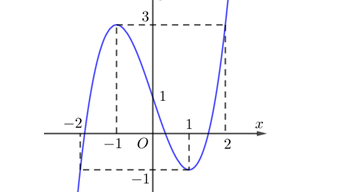
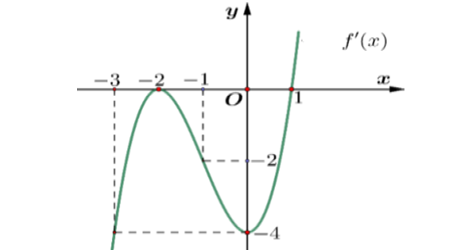
Question 17. (Chuyên Lam Sơn - Thanh Hóa 2025) Cho hàm đa thức $y=f(x)$ có đồ thị của hàm số $y=f'(x)$ là đường cong trong hình vẽ bên.

a) a) Hàm số $g(x)=f(x)-2025x+2024$ có đúng 2 điểm cực trị
b) b) $\min_{\mathbb{R}} f(x)=f(-1)$
c) c) Hàm số $f(x)$ nghịch biến trên khoảng (0;2)
d) d) Phương trình $f'(\cos x)=3$ có đúng 5 nghiệm thuộc $[0;\dfrac{5\pi}{2}]$

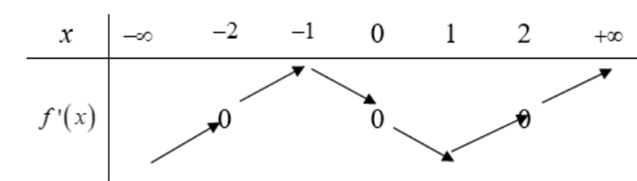
Question 18. (Cụm THPT Hoàn Kiếm - Hai Bà Trưng - Hà Nội 2025) Cho hàm số $y=f(x)$ xác định và có đạo hàm trên $\mathbb{R}$. Hàm số $y=f'(x)$ có bảng biến thiên như dưới đây

a) a) $\underset{[0;2]}{\text{Min}} f(x) = f(1)$
b) b) Trên [-2;2], hàm số đạt giá trị lớn nhất tại $x=0$
c) c) $\forall m \ge f(-2)$, phương trình $f(x)=m$ luôn có nghiệm trên [0;2]
d) d) Giá trị lớn nhất của $g(x)=f(x)-\sin^2 x$ trên đoạn [-1;1] là $f(0)$

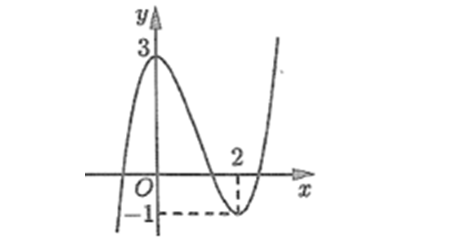
Question 19. (THPT Lương Tài 2 - Bắc Ninh 2025) Cho hàm số bậc ba $y = f(x)$ có đồ thị như hình vẽ.

a) Giá trị cực tiểu của hàm số đã cho bằng 2
b) Trên khoảng $(0;+\infty)$, giá trị nhỏ nhất của hàm số bằng -1
c) Hàm số nghịch biến trên khoảng (0;2)
d) Phương trình $f(x)-1=0$ có đúng hai nghiệm

Question 20. (THPT Gia Bình - Bắc Ninh 2025) Cho hàm số $y = \dfrac{1}{8}(x^3-3x^2-9x-5)$ có đồ thị là (C)

a) a) Phương trình tiếp tuyến có hệ số góc nhỏ nhất của đồ thị (C) đi qua điểm $A(0;-\dfrac{7}{3})$
b) b) Trên đoạn $[4;8]$ thì giá trị lớn nhất của hàm số đạt được tại $x = 4$
c) c) Tâm đối xứng của đồ thị hàm số có tọa độ là $(1;-2)$
d) d) Đồ thị hàm số có 2 điểm cực trị

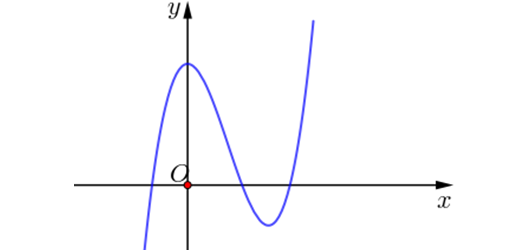
Question 21. (THPT Thạch Thành 1 - Thanh Hóa 2025) Cho đồ thị hàm số $y=f(x)$ có hình vẽ dưới đây và có tập xác định trên $\mathbb{R}$

a) a) Đồ thị hàm số đã cho là của hàm số $y = \dfrac{2x^2-1}{x+1}$
b) b) Hàm số đã cho không có giá trị lớn nhất và nhỏ nhất
c) c) Hàm số có đồ thị đã cho đồng biến trên $\mathbb{R}$
d) d) Đồ thị hàm số đã cho có hai cực trị

Question 22. (THPT Yên Lạc - Vĩnh Phúc 2025) Cho hàm số $f(x) = x^3-3x^2+5$. Đặt $g(x) = f(x)+mx$ (Với $m$ là tham số).

a) a) Hàm số $g(x)$ đạt cực trị khi và chỉ khi $m<3$
b) b) Hàm số $f(x)$ đồng biến trên khoảng $(3;+\infty)$
c) c) Đồ thị hàm số $f(x)$ cắt trục hoành tại 3 điểm phân biệt
d) d) Khi $m=-9$, giá trị lớn nhất của hàm $g(x)$ trên khoảng $(-\infty;0)$ bằng 10

Question 23. (THPT Thuận Thành 1&2 - Bắc Ninh 2025) Cho hàm số $y = f(x)$ có đạo hàm liên tục trên $\mathbb{R}$. Hàm số $y=f'(x)$ có đồ thị như hình dưới đây.

a) a) Hàm số $y=f(x)$ đồng biến trên khoảng $(1;+\infty)$
b) b) Trên đoạn $[-1;4]$ thì giá trị lớn nhất của hàm số $y=f(x)$ là $f(1)$
c) c) $f(1)>f(2)>f(4)$
d) d) Hàm số $y=f(x)$ có hai cực trị

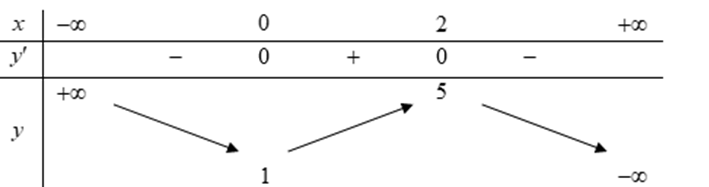
Question 24. (THPT Triệu Sơn 3 - Thanh Hóa 2025) Cho hàm số $y = f(x) = ax^3+bx^2+cx+d$ có bảng biến thiên như sau

a) a) Hàm số đồng biến trên khoảng (1;5)
b) b) Hàm số đạt cực đại tại điểm $x=2$
c) c) $a > 0$
d) d) Phương trình $2f(x)-e=0$ luôn có một nghiệm âm

Question 25. (THPT Triệu Sơn 4 - Thanh Hóa 2025) Cho hàm số $f(x)$ có đạo hàm $f'(x) = (x-1)^2(x^2-3x+2)$ với mọi $x \in \mathbb{R}$.

a) a) Hàm số đồng biến trên khoảng $(-\infty;2)$
b) b) Điểm cực đại của đồ thị hàm số là $x=1$
c) c) Hàm số $f(x)$ có hai điểm cực trị
d) d) Hàm số $y=f(x^2-4x+1)$ có ba điểm cực tiểu

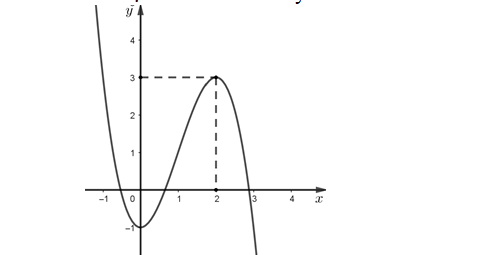
Question 26. (Chuyên Phan Bội Châu - Nghệ An 2025) Cho hàm số $f(x) = ax^3+bx^2+cx+d$ có đồ thị như hình sau đây

a) a) Giá trị cực tiểu của hàm số $f(x)$ bằng $-1$
b) b) Phương trình $\log_3(f(x)+6)=2$ có 2 nghiệm
c) c) Hàm số $y=f(x)$ đồng biến trên khoảng $(1;3)$
d) d) Tổng $2025a+b+c+d = -2023$

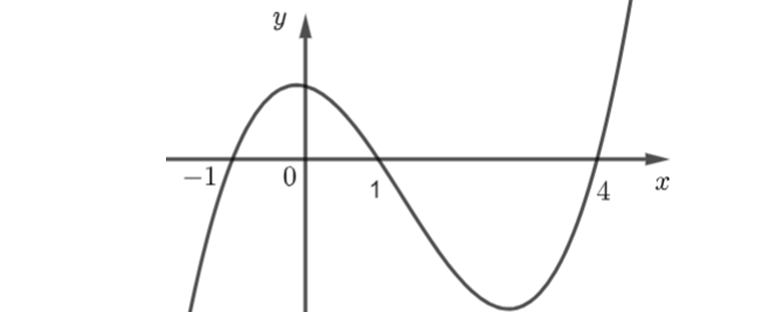
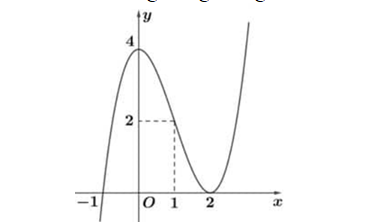
Question 27. (HSG Hải Phòng 2025) Cho hàm đa thức $y = f(x)$ có đồ thị của hàm số $y=f'(x)$ là đường cong trong hình vẽ bên.

a) a) Phương trình $f'(\cos x)=3$ có đúng 4 nghiệm thuộc $[0;\dfrac{5\pi}{2}]$
b) b) $\min_{\mathbb{R}} f(x) = f(-1)$
c) c) Hàm số $f(x)$ nghịch biến trên khoảng (0;2)
d) d) Hàm số $g(x) = f(x-2024)-2023x+2022$ có đúng 2 điểm cực trị

Question 28. (THPT Cụm trường Hải Dương 2025) Cho hàm số $f(x)$ có đạo hàm $f'(x)=(x-1)^2(x^2-3x+2)$ với mọi $x \in \mathbb{R}$.

a) a) Phương trình $f'(x)=0$ có duy nhất một nghiệm $x=2$
b) b) Hàm số $f(x)$ đồng biến trên khoảng $(-3;0)$
c) c) Hàm số $f(x)$ có hai điểm cực trị
d) d) Hàm số $y = f(x^2-6x+1)$ có ba điểm cực đại

Question 29. (THPT Cụm trường Hải Dương 2025) Cho hàm số $y=f(x)$ có đạo hàm trên $\mathbb{R}$ và hàm số $y=f'(x)$ là hàm số bậc ba có đồ thị là đường cong trong hình vẽ. Xét tính đúng sai của các khẳng định sau:

a) a) Hàm số $y=f(x)$ đồng biến trên khoảng $(-\infty;-2)$
b) b) Hàm số $y=f(x)$ có hai điểm cực trị
c) c) $f'(2)=4$
d) d) $g(x) = f(x) - \dfrac{1}{2}x^2+x+2024$ đồng biến trên khoảng $(-\dfrac{5}{2};\dfrac{3}{2})$

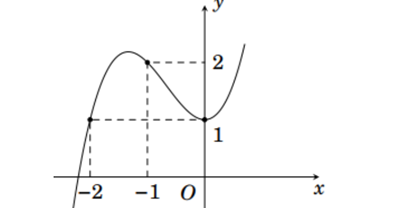
Question 30. (THPT Lê Xoay - Vĩnh Phúc 2025) Cho hàm số $y=f(x) = ax^3+bx^2+cx+d$ có đồ thị như hình dưới đây:

a) a) Trong 4 số $a,b,c,d$ có ba số dương
b) b) Hàm số đồng biến trên khoảng $(-\infty;-1)$
c) c) Đồ thị hàm số cắt Oy tại điểm có toạ độ (0;1)
d) d) Hàm số đạt cực tiểu tại $x=1$

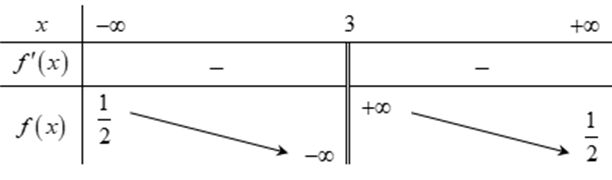
Question 31. (THPT Đào Duy Từ - Thanh Hóa 2025) Cho hàm số $y = \dfrac{2x+1}{x-1}$ có đồ thị (C).

a) a) Đồ thị (C) có tiệm cận đứng x=1 và tiệm cận ngang y=1
b) b) Hàm số đã cho nghịch biến trên các khoảng xác định của nó
c) c) Có đúng 3 điểm thuộc đồ thị (C) mà tọa độ của chúng là những số nguyên
d) d) Gọi M là điểm nằm trên đồ thị (C) và H, K tương ứng là hình chiếu vuông góc của M trên các trục Ox và Oy. Có 2 điểm M có hoành độ dương thỏa mãn tứ giác MHOK có diện tích bằng 2

Question 32. (THPT Hàm Rồng - Thanh Hóa 2025) Cho hàm số $f(x) = \dfrac{2x-3}{x^2+4}$

a) a) $f(24)=\dfrac{9}{116}$
b) b) Đồ thị hàm số $y=f(x)$ nhận trục hoành làm tiệm cận ngang
c) c) Hàm số $f(x)$ có điểm cực đại là $x=4$
d) d) Tập giá trị của hàm số đã cho là đoạn [a;b] thì $3a+4b=2$

Question 33. (THPT Lương Tài 2 - Bắc Ninh 2025) Cho hàm số $y = \dfrac{x^2-x+7}{x+1}$.

a) a) Đồ thị hàm số có hai điểm cực trị
b) b) Hàm số nghịch biến trên khoảng (-4;-1)
c) c) Đường tiệm cận xiên của đồ thị hàm số là đường thẳng $y=x-2$
d) d) Giá trị lớn nhất của hàm số trên khoảng $(-\infty;-1)$ bằng 3

Question 34. (THPT Văn Giang - Hưng Yên 2025) Cho hàm số $y=\dfrac{x^2+2x-1}{x-1}$ có đồ thị (C).

a) a) Hàm số có hai điểm cực trị
b) b) Đồ thị (C) có tiệm cận đứng là đường thẳng có phương trình $x=1$
c) c) Hàm số nghịch biến trên khoảng (0;2)
d) d) M là điểm bất kì thuộc đồ thị (C). Tích khoảng cách từ M đến tiệm cận đứng và tiệm cận xiên của đồ thị (C) bằng $\sqrt{2}$

Question 35. (THPT Tiên Du - Bắc Ninh 2025) Cho hàm số $y=f(x)=\dfrac{ax-1}{bx+c}$ với $a,b,c \in \mathbb{R}$ có bảng biến thiên như hình vẽ dưới đây

a) a) Đồ thị cắt trục tung tại điểm có tung độ nhỏ hơn $\dfrac{1}{2}$
b) b) Đồ thị hàm số có tiệm cận đứng $x=\dfrac{1}{2}$
c) c) Hàm số nghịch biến trên khoảng $(-\infty;3)$
d) d) $c \in (-\infty;-2) \cup (0;+\infty)$

Question 36. (THPT Nguyễn Đăng Đạo - Bắc Ninh 2025) Cho hàm số $y=f(x)=\dfrac{ax^2+bx+1}{cx+d}$ đạt cực đại tại $x=0$ và có đồ thị như hình vẽ sau:

a) a) Giá trị của biểu thức $a+b+c+d=0$
b) b) Hàm số đồng biến trên $(-1;0)$
c) c) Gọi A, B là các điểm cực trị của đồ thị hàm số; M là điểm di động trên trục Ox sao cho góc AMB không tù. Giá trị nhỏ nhất của hoành độ điểm M là 3
d) d) Đường thẳng đi qua hai điểm cực trị của hàm số có phương trình: $y=x-1$

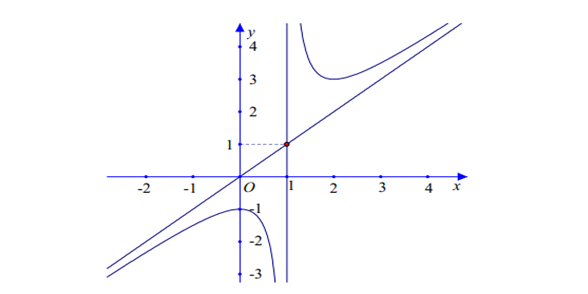
Question 37. (THPT Gia Bình - Bắc Ninh 2025) Cho hàm số $y=f(x)=\dfrac{ax^2+bx+c}{mx+n}$ (với $a,m \neq 0$) có đồ thị là đường cong như Hình

a) a) Hàm số đồng biến trên các khoảng $(-\infty;-3)$ và $(-1;+\infty)$
b) b) $f(2024) True
c) c) Đồ thị hàm số có tiệm cận đứng: $x=-3$ và đường tiệm cận xiên: $y=x+1$
d) d) Đồ thị hàm số đi qua điểm $A(2;\dfrac{13}{4})$

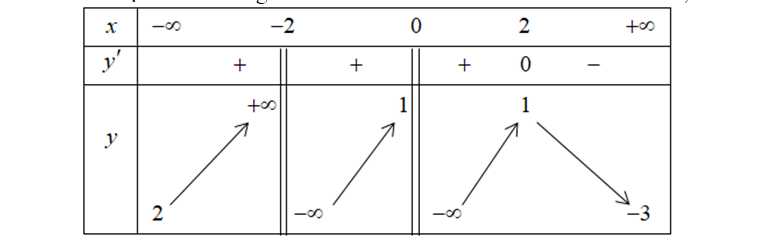
Question 38. (THPT Thạch Thành 1 - Thanh Hóa 2025) Cho hàm số $y=f(x)$ liên tục trên các khoảng xác định và có bảng biến thiên như hình vẽ sau: Xét tính ĐÚNG, SAI

a) a) Số đường tiệm cận đứng của đồ thị hàm số đã cho là 2
b) b) Đồ thị hàm số $y=f(x)$ có hai đường tiệm cận ngang $y=2; y=3$
c) c) Hàm số $y=f(x)$ nghịch biến trong khoảng $(1;+\infty)$
d) d) Hàm số $y=f(x)$ có hai điểm cực trị

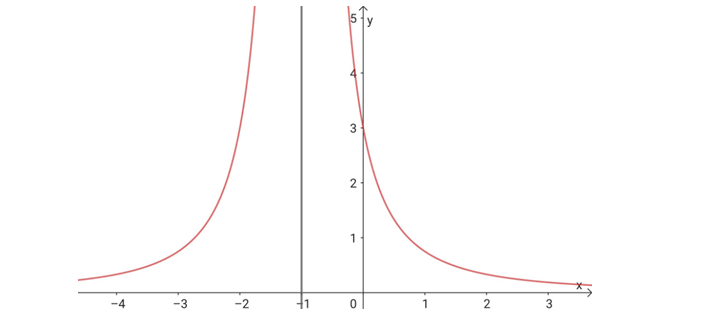
Question 39. (THPT Yên Lạc - Vĩnh Phúc 2025) Cho hàm số $f(x) = \begin{cases} \dfrac{3x-2}{2^{x-1}+1} & \text{khi } x>1
12 & \text{khi } x=1
\dfrac{x^2-3x-1}{x-1} & \text{khi } x<1 \end{cases}$

a) a) Ba đường tiệm cận của đồ thị hàm số cắt nhau tạo thành tam giác có diện tích bằng 50
b) b) Tiệm cận ngang của đồ thị hàm số là đường thẳng $y=12$
c) c) Hàm số liên tục tại điểm $x=1$
d) d) Đồ thị hàm số có tiệm cận đứng là đường thẳng $x=1$

Question 40. (THPT Chuyên Vĩnh Phúc 2025) Cho hàm số $f(x) = \dfrac{ax+b}{cx+d}$ với $a,b,c,d \in \mathbb{R}$ và $c \neq 0$ có đồ thị hàm số $y=f'(x)$ nhận đường thẳng $x=-1$ làm tiệm cận đứng như hình vẽ dưới. Biết rằng giá trị lớn nhất của hàm số $y=f(x)$ trên đoạn [-3;-2] bằng 8.

a) a) Giá trị nhỏ nhất của hàm số $y=f(x)$ trên đoạn [2;4] bằng 4
b) b) $f(-3)=8$
c) c) Hàm số $y=f(x)$ nghịch biến trên khoảng $(-1;+\infty)$
d) d) Đồ thị hàm số $y=f'(x)$ nhận đường thẳng $y=0$ làm tiệm cận ngang

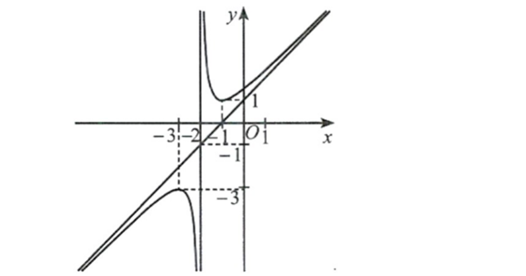
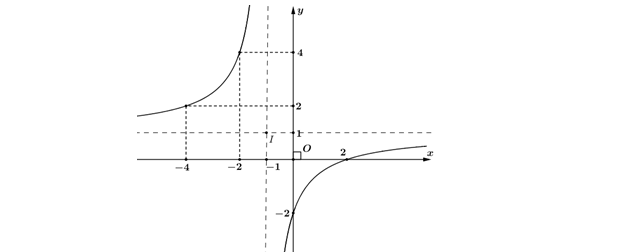
Question 41. (Sở Ninh Bình 2025) Cho hàm số $y=f(x)=\dfrac{ax^2+bx+c}{x+d}$ có đồ thị là đường cong trong hình vẽ dưới đây, biết đường tiệm cận xiên của đồ thị hàm số đi qua hai điểm (0;1) và (1;0).

a) a) Hàm số đồng biến trên khoảng (-4;0)
b) b) Ta có $a+b+c+d=-2$
c) c) Khoảng cách từ M(1;-8) đến đường thẳng đi qua các điểm cực trị của đồ thị hàm số là $\sqrt{5}$
d) d) Tập xác định của hàm số là $\mathbb{R}\setminus\{2\}$

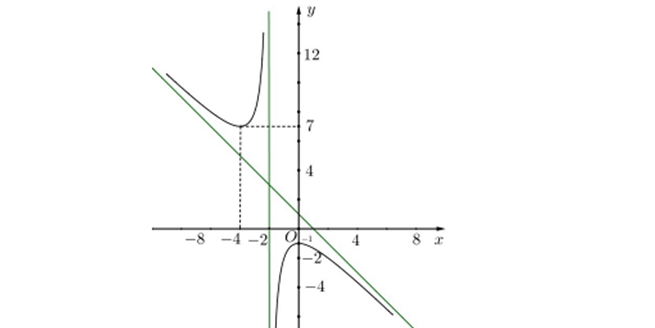
Question 42. (THPT Diễn Châu 5 - Nghệ An 2025) Cho hàm số $y=f(x)=\dfrac{ax^2+bx+c}{x+d}$ có đồ thị là đường cong như hình vẽ dưới đây, biết đường tiệm xiên của đồ thị hàm số đi qua hai điểm (0;1) và (1;0).

a) a) Tập xác định của hàm số là $\mathbb{R}\setminus\{2\}$
b) b) Hàm số đồng biến trên khoảng (-4;0)
c) c) Ta có $a+b+c+d=-2$
d) d) Khoảng cách từ M(1;-8) đến đường thẳng đi qua các điểm cực trị của đồ thị hàm số bằng $\sqrt{5}$

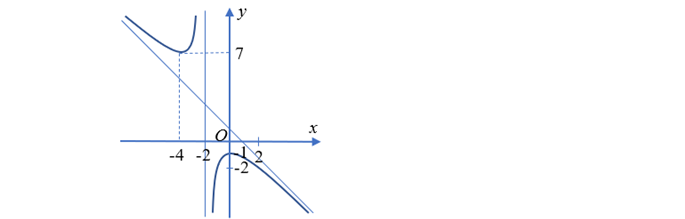
Question 43. (THPT Triệu Sơn 3 - Thanh Hóa 2025) Cho hàm số $y = \dfrac{x+1}{x-1}$ có đồ thị là đường cong (C). Giả sử A, B là hai điểm thuộc hai nhánh và AB đi qua tâm đối xứng của (C).

a) a) Tâm đối xứng của (C) là điểm I(1;-1)
b) b) Hàm số nghịch biến trên khoảng $(-\infty;1)$
c) c) Có 1 tiếp tuyến của đồ thị (C) song song với đường thẳng d : $y=-2x-1$
d) d) Giá trị nhỏ nhất của đoạn thẳng AB bằng $3\sqrt{2}$

Question 44. (Sở Bình Phước 2025) Cho hàm số $y = f(x)=ax+b+\dfrac{c}{x+d}$ ($a,b,c,d \in \mathbb{R}$) có đồ thị như hình vẽ sau:

a) a) Đồ thị hàm số đã cho có tiệm cận đứng là đường thẳng $x=-2$
b) b) Giá trị $f(0)=-5$
c) c) Đồ thị hàm số đã cho có tiệm cận xiên là đường thẳng $y=2x-4$
d) d) Hàm số đã cho là $y=-2x-4-\dfrac{2}{x+2}$

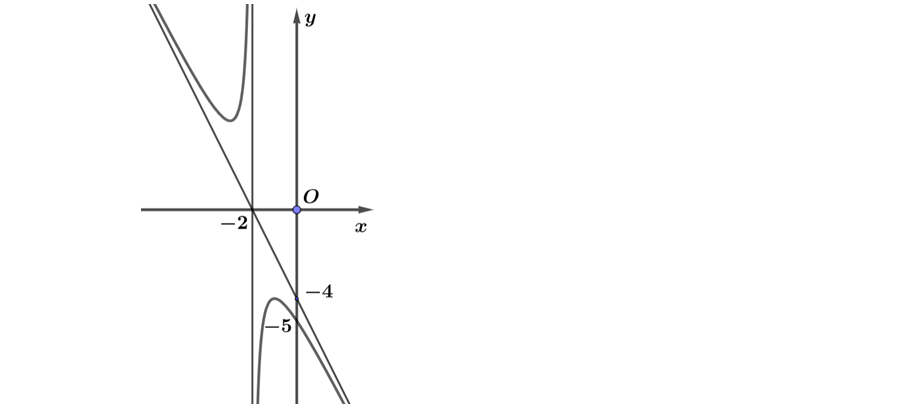
Question 45. (Cụm trường THPT Hải Dương 2025) Cho hàm số $y=\dfrac{x^2+bx+c}{x+n}$ có đồ thị và hai đường tiệm cận $d_1, d_2$ như hình vẽ dưới đây.

a) a) Đồ thị hàm số có tiệm cận đứng là $x=-1$
b) b) Hàm số đồng biến trên khoảng $(0;+\infty)$
c) c) Điểm M(50;98) và hai điểm cực trị của đồ thị hàm số thẳng hàng
d) d) Đồ thị hàm số có một trục đối xứng là đường thẳng $y=(p+\sqrt{q})(x+1)-r$ (trong đó p, q, r là các số nguyên). Khi đó $p+10q+15r=90$

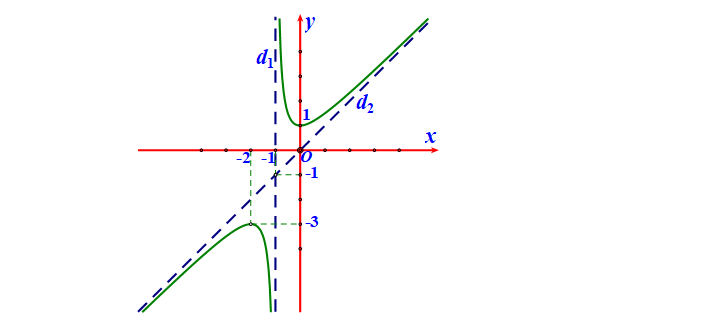
Question 46. (THPT Nguyễn Khuyến - Lê Thánh Tông 2025) Cho hàm số $y=\dfrac{ax^2+bx+c}{mx+n}$ có đồ thị như hình vẽ sau

a) a) Hàm số đã cho nghịch biến trên khoảng $(-2;0)$
b) b) Đồ thị của hàm số đã cho có tiệm cận xiên $y=x+1$
c) c) Gọi A, B là hai điểm cực trị của đồ thị hàm số đã cho, diện tích của tam giác OAB bằng 8 (với O là gốc tọa độ)
d) d) Một trục đối xứng của đồ thị đã cho là $d: y=(x+1)\tan\dfrac{3\pi}{8}$

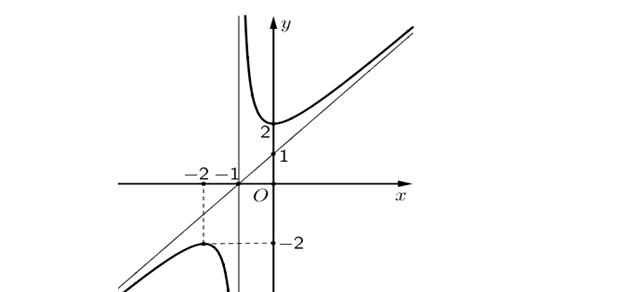
Question 47. (THPT Kinh Môn - Hải Dương 2025) Cho hàm số $y=\dfrac{x^2+3x+3}{x+2}$.

a) a) Hàm số đã cho đồng biến trên $(-\infty;-3)$ và $(-1;+\infty)$
b) b) Tổng giá trị cực đại và giá trị cực tiểu của hàm số đã cho bằng $-4$
c) c) Đường tiệm cận xiên của đồ thị hàm số đã cho đi qua điểm A(0;2)
d) d) Phương trình tiếp tuyến của đồ thị hàm số đã cho song song với đường thẳng $y=-3x-11$ đi qua điểm B(1;-6)

Question 48. (HSG Vũng Tàu 2025) Cho hàm số $y=\dfrac{x^2+3x-8}{x-2}$ (1) và đường tròn (C): $(x+3)^2+(y-1)^2=4$. Gọi I là tâm đường tròn (C).

a) a) Hàm số (1) đồng biến trên khoảng $(-\infty;0)$
b) b) Giá trị nhỏ nhất của hàm số (1) trên đoạn [3;5] bằng $7+2\sqrt{2}$
c) c) Tổng khoảng cách từ điểm I đến hai tiệm cận của đồ thị hàm số (1) bằng $\dfrac{10+3\sqrt{2}}{2}$
d) d) Đường thẳng đi qua hai điểm cực trị của đồ thị hàm số (1) cắt đường tròn (C) tại hai điểm phân biệt M, N. Diện tích tứ giác IMON bằng $\dfrac{14}{5}$ (với O là gốc tọa độ)

Question 49. (THPT Triệu Sơn 1-Thanh Hóa 2025) Cho hàm số $y = \dfrac{mx^2+nx+1}{px+2}$ có đồ thị như hình vẽ bên dưới. Các mệnh đề sau đúng hay sai?

a) a) Đường tiệm cận đứng của đồ thị là đường thẳng $x=-2$
b) b) Hàm số nghịch biến trên khoảng $(-2;+\infty)$
c) c) Đồ thị hàm số đi qua điểm A(0;1)
d) d) Ta có $2m+3n-p=10$

Question 50. (Cụm trường THPT Bắc Ninh 2025) Cho hàm số $y=\dfrac{2x+1}{x-1}$ (C). Các mệnh đề sau đây đúng hay sai

a) a) Hàm số $y=\dfrac{2x+1}{x-1}$ nghịch biến trên $\mathbb{R}\setminus\{1\}$
b) b) Hàm số đã cho có hai điểm cực trị
c) c) Tiếp tuyến với đồ thị (C) tại điểm có hoành độ bằng 2 tạo với hai trục tọa độ một tam giác có diện tích bằng $\dfrac{a}{b}$ (với $a,b \in \mathbb{N}$ và $(a,b)=1$). Khi đó $a-20b=1$
d) d) Lấy hai điểm A, B thuộc một nhánh của đồ thị (C) sao cho $x_A>1; x_B>1$ và hai điểm C,D thuộc đường thẳng $\Delta: y=-x+1$. Khi ABCD là hình vuông thì diện tích hình vuông đó (làm tròn đến hàng phần chục) là 23,7 đơn vị diện tích

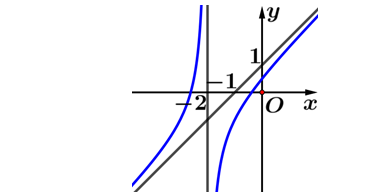
Question 51. (Chuyên Thái Bình 2025) Cho hàm số $y=f(x)=\dfrac{ax+b}{cx+1}$ với $a,b,c \in \mathbb{R}$ có đồ thị như hình vẽ dưới:

a) a) Đạo hàm của hàm số $f'(x)<0, \forall x \in \mathbb{R}$
b) b) Hàm số $y=f(x)$ nghịch biến trên khoảng $(1;+\infty)$ và đồng biến trên khoảng $(-\infty;1)$
c) c) Đồ thị hàm số $y=f(x)$ có đường tiệm cận đứng là $x=1$ và đường tiệm cận ngang là $y=-1$
d) d) Tổng $a+b+c=5$

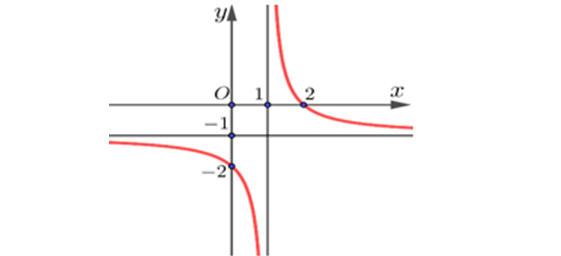
Question 52. (Sở Vĩnh Phúc 2025) Cho hàm số $y=\dfrac{3x-2}{x+2}$ có đồ thị (C).

a) a) Tiếp tuyến của đồ thị (C) tại giao điểm của đồ thị (C) với trục Oy là đường thẳng $y=2x+1$
b) b) Đồ thị (C) cắt đường thẳng $y=x-1$ tại hai điểm phân biệt
c) c) Đường thẳng $y=3$ là tiệm cận đứng của đồ thị hàm số
d) d) Điểm I(-2;3) là giao điểm của các đường tiệm cận của đồ thị (C)

Question 53. (THPT Sào Nam - Quảng Nam 2025) Cho hàm số $y=f(x)=\dfrac{x^2+2x-1}{x-1}$

a) a) Đường thẳng $y=x+3$ là tiệm cận xiên của đồ thị hàm số đã cho
b) b) Hàm số đồng biến trên khoảng $(-\infty;0)$
c) c) Giá trị lớn nhất của hàm số $y=f(x)$ trên đoạn $[-3;-1]$ là 1
d) d) Có 6 giá trị nguyên của m để phương trình $f(x)=m$ vô nghiệm

Question 54. (Cụm trường Nguyễn Hiền - Lê Hồng Phong - Quảng Nam 2025) Cho hàm số $y=\dfrac{x^2+x-1}{x-1}$ có đồ thị là (C). Xét tính đúng sai của các mệnh đề sau:

a) a) Tập xác định $D=\mathbb{R}\setminus\{1\}$ và đạo hàm $y'=\dfrac{x^2-2x-2}{(x-1)^2}$ với $x \neq 1$
b) b) Tâm đối xứng của đồ thị (C) là điểm I(1;3)
c) c) Giá trị nhỏ nhất của hàm số trên khoảng $(1;+\infty)$ bằng 5
d) d) Gọi A và B là hai điểm cực trị của (C). Khi đó $AB=4\sqrt{2}$

Question 55. (THPT Triệu Sơn 3 - Thanh Hóa 2025) Cho hàm số $y = \dfrac{x+1}{x-1}$ có đồ thị là đường cong (C). Giả sử A, B là hai điểm thuộc hai nhánh và AB đi qua tâm đối xứng của (C).

a) a) Tâm đối xứng của (C) là điểm I(1;-1)
b) b) Hàm số nghịch biến trên khoảng $(-\infty;1)$
c) c) Có 1 tiếp tuyến của đồ thị (C) song song với đường thẳng d : $y=-2x-1$
d) d) Giá trị nhỏ nhất của đoạn thẳng AB bằng $3\sqrt{2}$

Question 56. (Sở Bình Phước 2025) Cho hàm số $y = f(x)=ax+b+\dfrac{c}{x+d}$ ($a,b,c,d \in \mathbb{R}$) có đồ thị như hình vẽ sau:

a) a) Đồ thị hàm số đã cho có tiệm cận đứng là đường thẳng $x=-2$
b) b) Giá trị $f(0)=-5$
c) c) Đồ thị hàm số đã cho có tiệm cận xiên là đường thẳng $y=2x-4$
d) d) Hàm số đã cho là $y=-2x-4-\dfrac{2}{x+2}$

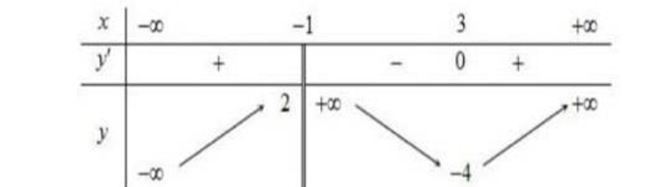
Question 57. (Cụm trường THPT Hải Dương 2025) Cho hàm số $y=\dfrac{x^2+bx+c}{x+n}$ có đồ thị và hai đường tiệm cận $d_1, d_2$ như hình vẽ dưới đây.

a) a) Đồ thị hàm số có tiệm cận đứng là $x=-1$
b) b) Hàm số đồng biến trên khoảng $(0;+\infty)$
c) c) Điểm M(50;98) và hai điểm cực trị của đồ thị hàm số thẳng hàng
d) d) Đồ thị hàm số có một trục đối xứng là đường thẳng $y=(p+\sqrt{q})(x+1)-r$ (trong đó p, q, r là các số nguyên). Khi đó $p+10q+15r=90$

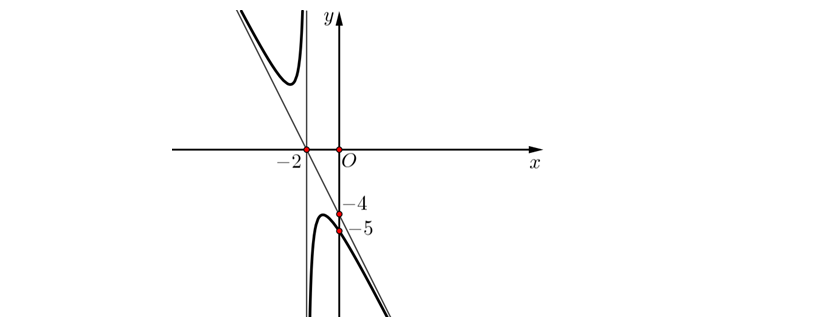
Question 58. (THPT Nguyễn Khuyến - Lê Thánh Tông 2025) Cho hàm số $y=\dfrac{ax^2+bx+c}{mx+n}$ có đồ thị như hình vẽ sau

a) a) Hàm số đã cho nghịch biến trên khoảng $(-2;0)$
b) b) Đồ thị của hàm số đã cho có tiệm cận xiên $y=x+1$
c) c) Gọi A, B là hai điểm cực trị của đồ thị hàm số đã cho, diện tích của tam giác OAB bằng 8 (với O là gốc tọa độ)
d) d) Một trục đối xứng của đồ thị đã cho là $d: y=(x+1)\tan\dfrac{3\pi}{8}$

Question 59. (THPT Kinh Môn - Hải Dương 2025) Cho hàm số $y=\dfrac{x^2+3x+3}{x+2}$.

a) a) Hàm số đã cho đồng biến trên $(-\infty;-3)$ và $(-1;+\infty)$
b) b) Tổng giá trị cực đại và giá trị cực tiểu của hàm số đã cho bằng $-4$
c) c) Đường tiệm cận xiên của đồ thị hàm số đã cho đi qua điểm A(0;2)
d) d) Phương trình tiếp tuyến của đồ thị hàm số đã cho song song với đường thẳng $y=-3x-11$ đi qua điểm B(1;-6)

Question 60. (HSG Vũng Tàu 2025) Cho hàm số $y=\dfrac{x^2+3x-8}{x-2}$ (1) và đường tròn (C): $(x+3)^2+(y-1)^2=4$. Gọi I là tâm đường tròn (C).

a) a) Hàm số (1) đồng biến trên khoảng $(-\infty;0)$
b) b) Giá trị nhỏ nhất của hàm số (1) trên đoạn [3;5] bằng $7+2\sqrt{2}$
c) c) Tổng khoảng cách từ điểm I đến hai tiệm cận của đồ thị hàm số (1) bằng $\dfrac{10+3\sqrt{2}}{2}$
d) d) Đường thẳng đi qua hai điểm cực trị của đồ thị hàm số (1) cắt đường tròn (C) tại hai điểm phân biệt M, N. Diện tích tứ giác IMON bằng $\dfrac{14}{5}$ (với O là gốc tọa độ)

Question 61. (THPT Triệu Sơn 1-Thanh Hóa 2025) Cho hàm số $y = \dfrac{mx^2+nx+1}{px+2}$ có đồ thị như hình vẽ bên dưới. Các mệnh đề sau đúng hay sai?

a) a) Đường tiệm cận đứng của đồ thị là đường thẳng $x=-2$
b) b) Hàm số nghịch biến trên khoảng $(-2;+\infty)$
c) c) Đồ thị hàm số đi qua điểm A(0;1)
d) d) Ta có $2m+3n-p=10$

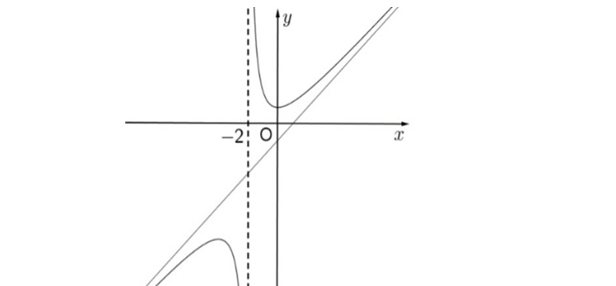
Question 62. (Cụm trường THPT Bắc Ninh 2025) Cho hàm số $y=\dfrac{2x+1}{x-1}$ (C). Các mệnh đề sau đây đúng hay sai

a) a) Hàm số $y=\dfrac{2x+1}{x-1}$ nghịch biến trên $\mathbb{R}\setminus\{1\}$
b) b) Hàm số đã cho có hai điểm cực trị
c) c) Tiếp tuyến với đồ thị (C) tại điểm có hoành độ bằng 2 tạo với hai trục tọa độ một tam giác có diện tích bằng $\dfrac{a}{b}$ (với $a,b \in \mathbb{N}$ và $(a,b)=1$). Khi đó $a-20b=1$
d) d) Lấy hai điểm A, B thuộc một nhánh của đồ thị (C) sao cho $x_A>1; x_B>1$ và hai điểm C,D thuộc đường thẳng $\Delta: y=-x+1$. Khi ABCD là hình vuông thì diện tích hình vuông đó (làm tròn đến hàng phần chục) là 23,7 đơn vị diện tích

Question 63. (Chuyên Thái Bình 2025) Cho hàm số $y=f(x)=\dfrac{ax+b}{cx+1}$ với $a,b,c \in \mathbb{R}$ có đồ thị như hình vẽ dưới:

a) a) Đạo hàm của hàm số $f'(x)<0, \forall x \in \mathbb{R}$
b) b) Hàm số $y=f(x)$ nghịch biến trên khoảng $(1;+\infty)$ và đồng biến trên khoảng $(-\infty;1)$
c) c) Đồ thị hàm số $y=f(x)$ có đường tiệm cận đứng là $x=1$ và đường tiệm cận ngang là $y=-1$
d) d) Tổng $a+b+c=5$

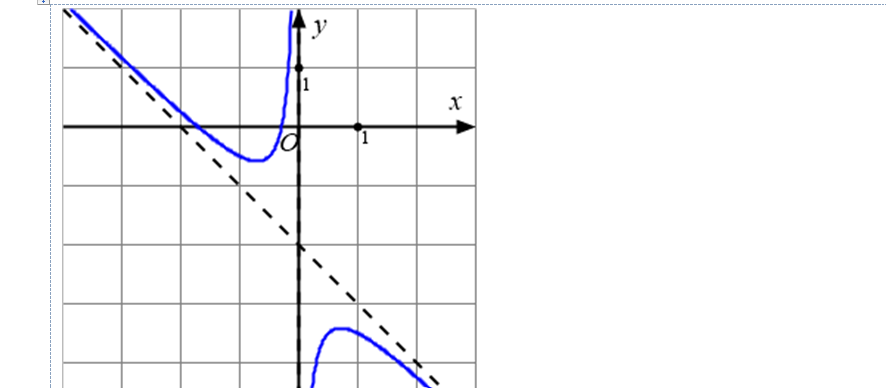
Question 64. (Sở Vĩnh Phúc 2025) Cho hàm số $y=\dfrac{3x-2}{x+2}$ có đồ thị (C).

a) a) Tiếp tuyến của đồ thị (C) tại giao điểm của đồ thị (C) với trục Oy là đường thẳng $y=2x+1$
b) b) Đồ thị (C) cắt đường thẳng $y=x-1$ tại hai điểm phân biệt
c) c) Đường thẳng $y=3$ là tiệm cận đứng của đồ thị hàm số
d) d) Điểm I(-2;3) là giao điểm của các đường tiệm cận của đồ thị (C)

Question 65. (THPT Sào Nam - Quảng Nam 2025) Cho hàm số $y=f(x)=\dfrac{x^2+2x-1}{x-1}$

a) a) Đường thẳng $y=x+3$ là tiệm cận xiên của đồ thị hàm số đã cho
b) b) Hàm số đồng biến trên khoảng $(-\infty;0)$
c) c) Giá trị lớn nhất của hàm số $y=f(x)$ trên đoạn $[-3;-1]$ là 1
d) d) Có 6 giá trị nguyên của m để phương trình $f(x)=m$ vô nghiệm

Question 66. (Cụm trường Nguyễn Hiền - Lê Hồng Phong - Quảng Nam 2025) Cho hàm số $y=\dfrac{x^2+x-1}{x-1}$ có đồ thị là (C). Xét tính đúng sai của các mệnh đề sau:

a) a) Tập xác định $D=\mathbb{R}\setminus\{1\}$ và đạo hàm $y'=\dfrac{x^2-2x-2}{(x-1)^2}$ với $x \neq 1$
b) b) Tâm đối xứng của đồ thị (C) là điểm I(1;3)
c) c) Giá trị nhỏ nhất của hàm số trên khoảng $(1;+\infty)$ bằng 5
d) d) Gọi A và B là hai điểm cực trị của (C). Khi đó $AB=4\sqrt{2}$

Question 67. (THPT Nông Cống 3 - Thanh Hóa 2025) Cho hàm số $y = \dfrac{x^2-3x+6}{x-1}$

a) a) Điểm cực tiểu của đồ thị hàm số là (a;b) với $a^2+b=12$
b) b) Tiệm cận xiên của đồ thị hàm số là $y=x-2$
c) c) Gọi I là giao điểm hai đường tiệm cận của đồ thị hàm số. Tiếp tuyến của đồ thị hàm số tại điểm có hoành độ x=2 cắt hai đường tiệm cận tại A, B. Diện tích tam giác IAB bằng 12
d) d) Có tất cả 9 giá trị nguyên của tham số m để phương trình $\dfrac{x^2-3x+6}{x-1}=m$ có hai nghiệm phân biệt $x_1, x_2$ thỏa mãn $x_1<2 True

Question 68. (THPT Trực Ninh - Nam Định 2025) Cho hàm số $y=\dfrac{-x^2-3x+4}{x-3}$ có đồ thị là (C).

a) a) Đồ thị (C) có hai điểm cực trị nằm 2 phía đối với Oy
b) b) Đồ thị (C) có tiệm cận xiên là $y=-x-6$
c) c) Đồ thị (C) nhận giao điểm I(3;-9) làm tâm đối xứng
d) d) Đồ thị không cắt trục Ox

Question 69. (THPT Lê Thánh Tông - Nguyễn Khuyến HCM 2025) Cho hàm số $y=f(x) = \dfrac{2x-3}{x-6}$ có đồ thị (C).

a) a) Đường thẳng $x=-6$ là tiệm cận ngang của đồ thị (C)
b) b) $f'(x)<0, \forall x \in (6;+\infty)$
c) c) Hàm số đã cho không có điểm cực trị
d) d) Hàm số đã cho nghịch biến trên khoảng $(0;+\infty)$

Question 70. (Sở Bắc Giang 2025) Cho hàm số $y=f(x)$ có bảng biến thiên như sau

a) a) Đồ thị hàm số $y=f(x)$ có đúng hai đường tiệm cận
b) b) Hàm số $y=f(x)$ đồng biến trên khoảng $(3;+\infty)$
c) c) Hàm số $y=f(x)$ có đúng một điểm cực trị
d) d) Giá trị nhỏ nhất của $h(x)=2f(x)+2025x$ trên đoạn [3;2025] bằng 6083

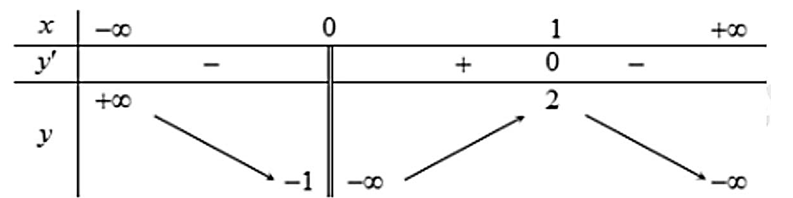
Question 71. (Sở Thái Nguyên 2025) Cho hàm số $y=f(x)=\dfrac{x^2+x-1}{x+2}$.

a) a) Tập xác định của hàm số $y=f(x)$ là $\mathbb{R}\setminus\{-2\}$
b) b) Tâm đối xứng của đồ thị hàm số $y=f(x)$ là điểm I(2;1)
c) c) Đồ thị hàm số $y=f(x)$ có hai điểm cực trị nằm cùng phía đối với trục hoành
d) d) Gọi M là giao điểm của đồ thị hàm số $y=f(x)$ với trục tung. Phương trình tiếp tuyến của đồ thị hàm số tại điểm M là $y=\dfrac{3}{4}x-\dfrac{1}{2}$

Question 72. (KHTN Hà Nội 2025) Cho hàm số $f(x)=\dfrac{x^2-x-1}{x+1}$ và điểm $A(-1;-3)$.

a) a) Hàm số $f(x)$ có đúng 2 điểm cực trị
b) b) Hàm số $f(x)$ nghịch biến trên khoảng (–2;0)
c) c) Đường thẳng $y=x-2$ là đường tiệm cận xiên của đồ thị hàm số $y=f(x)$
d) d) Xét điểm M thuộc đồ thị hàm số $y=f(x)$, đoạn thẳng AM có độ dài luôn lớn hơn 2,2

Question 73. (Cụm trường THPT Hải Dương 2025) Cho hàm số $y = \dfrac{x^2-3x+6}{x-1}$

a) a) Điểm cực tiểu của đồ thị hàm số là (a;b) với $a^2+b=12$
b) b) Tiệm cận xiên của đồ thị hàm số là $y=x-2$
c) c) Gọi I là giao điểm hai đường tiệm cận của đồ thị hàm số. Tiếp tuyến của đồ thị hàm số tại điểm có hoành độ x=2 cắt hai đường tiệm cận tại A, B. Diện tích tam giác IAB bằng 12
d) d) Có tất cả 9 giá trị nguyên của tham số m để phương trình $\dfrac{x^2-3x+6}{x-1}=m$ có hai nghiệm phân biệt $x_1, x_2$ thỏa mãn $x_1<2 True

Question 74. (Sở Bạc Liêu 2025) Cho hàm số $y=\dfrac{2x+1}{x-1}$ có đồ thị (C).

a) a) Hàm số đạt cực đại tại $x=-3$
b) b) Giá trị lớn nhất của hàm số trên [2;4] bằng 5
c) c) Đường thẳng $x=1$ là tiệm cận đứng của đồ thị (C)
d) d) Hàm số đồng biến trên khoảng $(-\infty;1)$ và $(1;+\infty)$

Question 75. (Chuyên KHTN Hà Nội 2025) Cho hàm số $y=\dfrac{x^2-2x-3}{x-1}$

a) a) Đồ thị hàm số nhận đường thẳng $y=x+1$ làm tiệm cận xiên
b) b) Hàm số có 2 điểm cực trị
c) c) Gọi A,B,C là giao điểm của đồ thị hàm số với các trục Ox,Oy. Diện tích tam giác ABC bằng 6
d) d) Có đúng 2 giá trị nguyên của tham số m để hàm số $f(x)=\dfrac{x^2-2x-3}{x-1}-m^2x$ đồng biến trên từng khoảng xác định

Question 76. (THPT Triệu Sơn 1 - Thanh Hóa 2025) Cho hàm số $y=f(x)=\dfrac{x^2+x-m}{x-2}$, có đồ thị $(C_m)$ (với m là tham số thực). Khi đó:

a) a) Đồ thị $(C_m)$ luôn có hai điểm cực trị
b) b) Khi $m=5$ thì hàm số $f(x)$ đồng biến trên khoảng $(3;+\infty)$
c) c) Hàm số $f(x)$ nghịch biến trên $\mathbb{R}$
d) d) Hàm số $f(x)$ có hai điểm cực trị khi $m>6$

Question 77. (Chuyên Phan Bội Châu - Hà Tĩnh 2025) Cho hàm số $y=ax+b+\dfrac{c}{x+d}$ ($a,b,c,d \in \mathbb{R}$) có đồ thị như hình vẽ sau:

a) a) Đồ thị hàm số đã cho có tiệm cận đứng là đường thẳng $x=-2$
b) b) Giá trị $b=-4$
c) c) Đồ thị hàm số đã cho có tiệm cận xiên là đường thẳng $y=2x-4$
d) d) Hàm số đã cho là $y=-2x-4-\dfrac{2}{x+2}$

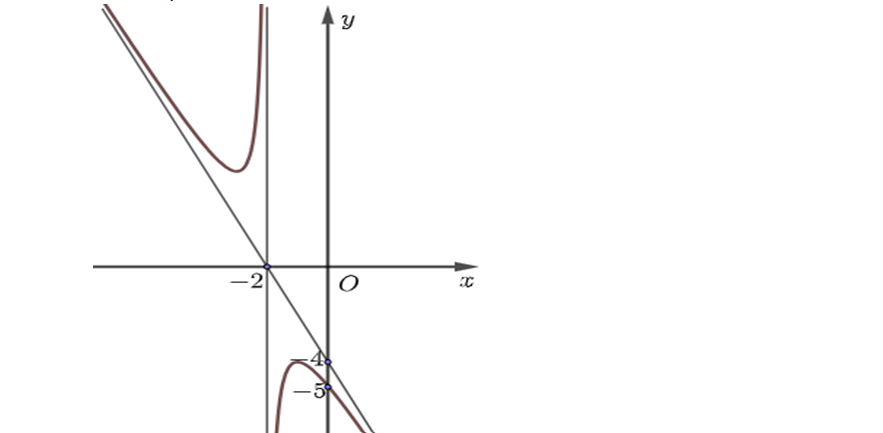
Question 78. (THPT Anh Sơn 3 - Nghệ An 2025) Cho hàm số $f(x)=-x+4-\dfrac{9}{x+2}$.

a) a) $f(-7)=\dfrac{64}{5}; f(-4)=\dfrac{25}{2}$
b) b) Đồ thị của hàm số đã cho có đường tiệm cận đứng $x=-2$
c) c) Đạo hàm của hàm số đã cho $f'(x)=\dfrac{-x^2-4x-5}{(x+2)^2}$
d) d) Giá trị nhỏ nhất của hàm số đã cho trên đoạn [-7;–4] là $\dfrac{25}{2}$

Question 79. (THPT Đô Lương 1 - Nghệ An 2025) Cho hàm số $f(x)=\dfrac{x^2+2x-1}{x-1}$.

a) a) Hàm số đồng biến trên khoảng $(-\infty;0)$
b) b) Đường thẳng $y=x+3$ là tiệm cận xiên của đồ thị hàm số đã cho
c) c) Tâm đối xứng của đồ thị hàm số đã cho là I(1;3)
d) d) Giá trị lớn nhất của hàm số trên đoạn $[-3;-1]$ là 1

Question 80. (Sở Sơn La 2025) Cho hàm số $f(x)=\dfrac{x^2-3x+3}{x-1}$.

a) a) Tập xác định của hàm số là $D=(-\infty;1) \cup (1;+\infty)$
b) b) Hàm số đã cho đồng biến trên khoảng $(3;+\infty)$
c) c) Đường tiệm cận xiên của đồ thị hàm số đã cho là đường thẳng $y=x+2$
d) d) Khoảng cách giữa hai điểm cực trị của đồ thị hàm số đã cho là $5\sqrt{2}$

Question 81. (THPT Ngô Sĩ Liên - Bắc Giang 2025) Cho hàm số $y=\dfrac{x^2+2x-1}{x-1}$ có đồ thị (C).

a) a) Hàm số có 2 điểm cực trị
b) b) Hàm số nghịch biến trên khoảng (0;2)
c) c) Đồ thị (C) có tiệm cận đứng là đường thẳng có phương trình $x=1$
d) d) M là điểm bất kì thuộc đồ thị (C). Tích khoảng cách từ M đến tiệm cận đứng và tiệm cận xiên của đồ thị (C) bằng $\sqrt{2}$

Question 82. (Sở Quảng Ninh 2025) Cho hàm số $y=x-1+\dfrac{9}{x+2}$

a) a) Tập xác định của hìm số là: $\mathbb{R}\setminus\{-2\}$
b) b) Hàm số có đạo hàm là $y'=1-\dfrac{9}{(x+2)^2}; \forall x \neq -2$
c) c) Hàm số đồng biến trên các khoàng $(-\infty;-5)$ và $(1;+\infty)$
d) d) Hàm số có giá trị cuc đại lớn hơn giá trị cực tiểu

Question 83. (Cụm Ninh Giang - Tứ Kỳ - Gia Lộc 2025) Cho hàm số $y=\dfrac{-x^2+x+1}{x+1}$ có đồ thị (C).

a) a) Gọi (C') là đường tròn tâm $I(-1;3)$, bán kính bằng 1. Khoảng cách nhỏ nhất giữa hai điểm M,N với $M \in (C)$ và $N \in (C')$ bằng $1+2\sqrt{2}$
b) b) Đường thẳng nối hai điểm cực trị của đồ thị (C) cắt hai trục tọa độ tại hai điểm A và B. Khi đó diện tích tam giác OAB là $S=\dfrac{1}{2}$
c) c) Hàm số đồng biến trên các khoảng $(-2;-1)$ và $(-1;0)$
d) d) Tiệm cận đứng của đồ thị (C) là đường thẳng có phương trình $x=-1$

Question 84. (THPT Mai Trúc Loan - Hà Tĩnh 2025) Cho hàm số $f(x) = \dfrac{2x^2-3x}{e^x}$.

a) a) Tập xác định của hàm số đã cho là $D=\mathbb{R}\setminus\{0\}$
b) b) $f'(x) = \dfrac{-2x^2+7x-3}{e^{2x}}$
c) c. Phương trình $f'(x)=0$ có hai nghiệm phân biệt trong (0;4)
d) d. Giá trị lớn nhất của hàm số đã cho trong (0;4) bằng $\dfrac{9}{e^3}$

Question 85. (THPT Quế Võ 1 - Bắc Ninh 2025) Cho hàm số $y=f(x)=\dfrac{x^2+2x-2}{x-1}$ có đồ thị (C). Các khẳng định sau đây đúng hay sai?

a) a) Hàm số đã cho nghịch biến trên khoàng (0;2)
b) b) Đường tiệm cận xiên của (C) có phương trình là $y=x+3$
c) c) Giả trị nhỏ nhất của hàm số $y=f(x)$ trên đoạn [2;4] bằng $\dfrac{13}{2}$
d) d) Có 3 số nguyên dương m để hàm số $y=\dfrac{x^2+2x-m}{x-1}$ có hai điểm cực trị

Question 86. (Cụm Chương Mỹ - Thanh Oai 2025) Cho hàm số $y=f(x)=\dfrac{-x^2+x-2}{x+1}$ có đồ thị (C). Khi đó

a) a) $y'=f'(x) = \dfrac{-x^2-2x+3}{(x+1)^2}, \forall x \neq -1$
b) b) Hàm số có hai điểm cực trị trái dấu
c) c) Khoảng cách giữa hai điểm cực trị của đồ thị (C) bằng 4
d) d) Trên đồ thị (C) có đúng 8 điểm có tọa độ nguyên

Question 87. (THPT Hà Trung - Thanh Hóa 2025) Cho hàm số $y=\dfrac{3x+2}{x+2}$ có đồ thị là (C). Hai điểm A,B thuộc hai nhánh của đồ thị (C).

a) a) Giá trị nhỏ nhất của hàm số $y=\dfrac{3x+2}{x+2}$ trên đoạn [2;5] là 2
b) b) Khi độ dài đoạn AB ngắn nhất thì $OA.OB=\sqrt{29}$
c) c) Hàm số đồng biến trên $\mathbb{R}\setminus\{-2\}$
d) d) Đường thẳng $y=3$ là tiệm cận ngang của đồ thị (C)

Question 88. Cho hàm số $y=f(x)=x+2+\dfrac{1}{x-1}$.

a) a) Tập xác định của hàm số $D=\mathbb{R}\setminus\{1\}$
b) b) Tiệm cận xiên của đồ thị hàm số là đường thẳng $y=f(x)=x-2$
c) c) Hàm số nghịch biến trên tập xác định
d) d.Đồ thị hàm số có 2 điểm cực trị là A, B. Khoảng cách từ gốc tọa độ đến đường thẳng AB là $\dfrac{1}{\sqrt{5}}$

Question 89. (Sở Bình Phước 2025) Cho hàm số $f(x)=\dfrac{2x^2+3x-5}{x+3}$

a) a) Hàm số có đạo hàm $f'(x)=\dfrac{2x^2+12x-14}{(x+3)^2}$
b) b) Tiệm cận xiên của đồ thị hàm số đã cho là đường thẳng $\Delta: y=2x-3$
c) c) Đồ thị hàm số nhận điểm I(3;3) làm tâm đối xứng
d) d) Đường tiệm cận xiên của đồ thị hàm số $f(x)=\dfrac{2x^2+3x-5}{x+3}$ cắt trục hoành, trục tung lần lượt tại A, B. Khi đó diện tích của tam giác OAB lớn hơn 2

Question 90. (THPT Lê Quý Đôn - Hà Nội 2025) Cho hàm số $f(x)=\dfrac{2x-3}{x^2+4}$

a) a) Tập giá trị của hàm số đã cho là đoạn [a;b] thì $3a+4b=5$
b) b) Hàm số $f(x)$ có hai điểm cực trị
c) c) Đồ thị hàm số $y=f(x)$ nhận trục tung làm tiệm cận ngang
d) d) $f(0)=-\dfrac{3}{4}$

Question 91. (Sở Hải Phòng 2025) Cho hàm số $y=\dfrac{x^2+3x+3}{x+2}$ có đồ thị (C) và 2 điểm A, B là hai điểm cực trị của (C).

a) a) $y'=\dfrac{x^2+4x+3}{(x+2)^2}$
b) b) 2 điểm A và B nằm ở hai phía của trục tung
c) c) Đường thẳng AB có phương trình là $y=2x+1$
d) d) A và B đối xứng nhau qua đường thẳng $\Delta$ có phương trình là $x+2y+4=0$

Question 92. (Sở Gia Lai 2025) Cho hàm số $y=\dfrac{x^2-2x+2}{x-1}$.

a) a) Hàm số đã cho được viết lại $y=x-1+\dfrac{1}{x-1}$
b) b) Phương trình $y'=0$ có hai nghiệm $x_1=2$ và $x_2=0$
c) c) Hàm số đã cho nghịch biến trên khoảng (0;2)
d) d) Đồ thị của hàm số là hình vẽ dưới đây

Question 93. (THPT Lê Thánh Tông - HCM 2025) Cho hàm số $f(x) = 4\sin x\cos x + 2x$.

a) a) Đạo hàm của hàm số đã cho là $f'(x) = 4\sin 2x+2$
b) b) Hàm số $y = f(x)$ có 4 điểm cực trị thuộc $[-\pi;\pi]$
c) c) Hàm số $y=f(x)$ đồng biến trên khoảng $(-2;-1)$
d) d) Giá trị lớn nhất của $f(x)$ trên đoạn $\left[0;\dfrac{\pi}{2}\right]$ là $\dfrac{2\pi}{3}+\sqrt{3}$

Question 94. (Đề Tham Khảo 2025) Cho hàm số $f(x) = 2\cos x+x$.

a) a) $f(0)=2; f(\dfrac{\pi}{2})=\dfrac{\pi}{2}$
b) b) Đạo hàm của hàm số đã cho là $f'(x)=2\sin x+1$
c) c) Nghiệm của phương trình $f'(x)=0$ trên đoạn $\left[0;\dfrac{\pi}{2}\right]$ là $\dfrac{\pi}{6}$
d) d) Giá trị lớn nhất của $f(x)$ trên đoạn $\left[0;\dfrac{\pi}{2}\right]$ là $\sqrt{3}+\dfrac{\pi}{6}$

Question 95. (THPT Nguyễn Viết Xuân - Vĩnh Phúc 2025) Cho hàm số $f(x)=\sin x-x$.

a) a) Đạo hàm của hàm số đã cho là $f'(x)=\cos x-1$
b) b) Nghiệm của phương trình $f'(x)=0$ trên đoạn $\left[\dfrac{\pi}{2};\dfrac{3\pi}{2}\right]$ là $\pi$
c) c) Giá trị nhỏ nhất của $f(x)$ trên đoạn $\left[\dfrac{\pi}{2};\dfrac{3\pi}{2}\right]$ là $-1-\dfrac{3\pi}{2}$
d) d) $f(0)=0; f(\pi)=-\pi$

Question 96. (THPT Thuận Thành 1\&2 - Bắc Ninh 2025) Cho hàm số $f(x)=2\sin x - \sqrt{3}x$.

a) a) Một nghiệm của phương trình $f'(x)=0$ là $x=-\dfrac{\pi}{3}$
b) b) $f\left(\dfrac{\pi}{2}\right)=-\dfrac{\pi\sqrt{3}}{2}$
c) c) Đạo hàm của hàm số là $f'(x)=2\cos x - \sqrt{3}, \forall x \in \mathbb{R}$
d) d) Tổng các nghiệm của phương trình $f'(x)=0$ trong đoạn $\left[0;\dfrac{5\pi}{2}\right]$ bằng $\dfrac{25\pi}{6}$

Question 97. (THPT Diễn Châu 5 - Nghệ An 2025) Xét hàm số $y=\dfrac{x}{2}-\sin^2 x$ trên khoảng $(0;\pi)$. Xét tính đúng sai của các mệnh đề sau:

a) a) Hàm số nghịch biến trên khoảng $\left(\dfrac{5\pi}{12};\pi\right)$
b) b) Hàm số có 2 điểm cực trị
c) c) Giá trị cực tiểu của hàm số là $\dfrac{5\pi}{24}-\dfrac{2+\sqrt{3}}{4}$
d) d) Đồ thị hàm số $y=f'(x)$ cắt đồ thị hàm số $y=-\dfrac{\sin^2 2x}{2}$ tại 2 nghiệm trên khoảng $(0;\pi)$

Question 98. (THPT Hùng Vương - Bình Thuận 2025) Cho hàm số $f(x)=\sin 2x-x$.xét tính đúng sai của các khẳng định sau

a) a) $f\left(-\dfrac{\pi}{2}\right) = f\left(\dfrac{\pi}{2}\right)=-\dfrac{\pi}{2}$
b) b) Đạo hàm của hàm số đã cho là $f'(x)=\cos 2x-1$
c) c) Nghiệm của phương trình $f'(x)=0$ trên đoạn $\left[-\dfrac{\pi}{2};\dfrac{\pi}{2}\right]$ là $\dfrac{\pi}{6}$ hoặc $-\dfrac{\pi}{6}$
d) d) Giá trị nhỏ nhất của $f(x)$ trên đoạn $\left[-\dfrac{\pi}{2};\dfrac{\pi}{2}\right]$ là $-\dfrac{\pi}{2}$

Question 99. (THPT Lê Lợi - Thanh Hóa 2025) Cho hàm số $f(x)=2\sin 2x+2x$.

a) a) Đạo hàm của hàm số đã cho là $f'(x)=4\sin 2x+2$
b) b) Phương trình $f'(x)=0$ có 2 nghiệm thuộc $[0;\pi]$
c) c) $f(\pi)=\pi$
d) d) Giá trị lớn nhất của $f(x)$ trên đoạn $\left[0;\dfrac{\pi}{2}\right]$ là $\dfrac{2\pi}{3}+\sqrt{3}$

Question 100. (THPT Triệu Sơn 1-Thanh Hóa 2025) Cho hàm số $f(x)=\sin x - \sqrt{3}\cos x-2$. Các mệnh đề sau đúng hay sai?

a) a) $f\left(\dfrac{\pi}{2}\right)=-1$
b) b) Đạo hàm của hàm số đã cho là $f'(x)=\cos x - \sqrt{3}\sin x$
c) c) Nghiệm của phương trình $f'(x)=0$ trên đoạn $[0;\pi]$ là $\dfrac{5\pi}{6}$
d) d) Giá trị lớn nhất của $f(x)$ trên đoạn $[0;\pi]$ là $\sqrt{3}-2$

Question 101. (Chuyên Hạ Long 2025) Cho hàm số $f(x)=\sin 2x-x$ xác định trên $\mathbb{R}$.

a) a) $f\left(\dfrac{\pi}{2}\right)=-\dfrac{\pi}{2}$
b) b) $f'(x)=\cos 2x-1$
c) c) $f'(x)=0 \Leftrightarrow x = \pm\dfrac{\pi}{6}+k2\pi, k \in \mathbb{Z}$
d) d) Phương trình $f'(x)=0$ có đúng 2 nghiệm thuộc khoảng $(0;\pi)$

Question 102. (Sở Thanh Hóa 2025) Cho hàm số $f(x)=2\sin x+1$

a) a) Giá trị nhỏ nhất của $f(x)$ là $-1$
b) b) Hàm số $f(0)=1; f\left(\dfrac{\pi}{2}\right)=3$
c) c) Nghiệm của phương trình $f'(x)=0$ trên đoạn $\left[0;\dfrac{\pi}{2}\right]$ là $\dfrac{\pi}{4}$
d) d) Đạo hàm của hàm số đã cho là $f'(x)=2\cos x+1$

Question 103. (Chuyên Lê Khiết - Quảng Ngãi 2025) Cho hàm số $f(x)=2\sin x+x$

a) a) $f(0)=0; f(\pi)=\pi$
b) b) Đạo hàm của hàm số đã cho là $f'(x)=-2\cos x+1$
c) c) Số nghiệm của phương trình $f'(x)=0$ trên đoạn $[0;3\pi]$ là 6
d) d) Giá trị lớn nhất của $f(x)$ trên đoạn $[0;\pi]$ là $\dfrac{2\pi}{3}+\sqrt{3}$

Question 104. (THPT Nông Cống 3 - Thanh Hóa 2025) Cho hàm số $f(x)=\sin^2 x + \cos x-1$. Khi đó

a) a) Nghiệm dương bé nhất của phương trình $f(x)=0$ là $\dfrac{\pi}{2}$
b) b) $f'(x)=2\sin x-\sin x$
c) c) Gọi giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y=f(x)$ trên $\left[\dfrac{\pi}{2};\dfrac{3\pi}{4}\right]$ lần lượt là M, m. Khi đó $M+m=\dfrac{-1-2\sqrt{2}}{4}$
d) d) $f(-\pi)=-f(\pi)$

Question 105. (THPT Lê Hồng Phong - Hải Phòng 2025) Cho hàm số $f(x) = 2\cos x+x\sqrt{2}$.

a) a) Đạo hàm của hàm số đã cho là $f'(x) = 2\sin x+\sqrt{2}$
b) b) $f(0)=2; f(\pi)=-2+\pi\sqrt{2}$
c) c) Tổng giá trị lớn nhất và giá trị nhỏ nhất của $f(x)$ trên đoạn $[0;\pi]$ là $\pi\sqrt{2}$
d) d) Phương trình $f'(x)=0$ có đúng hai nghiệm trên đoạn $[0;\pi]$

Question 106. (Sở Quảng Bình 2025) Cho hàm số $f(x)=\sin 2x-x$.

a) a) $f\left(-\dfrac{\pi}{2}\right) = \dfrac{\pi}{2}; f\left(\dfrac{\pi}{2}\right)=-\dfrac{\pi}{2}$
b) b) Đạo hàm của hàm số đã cho là $f'(x)=\cos 2x-1$
c) c) Phương trình $f'(x)=0$ có hai nghiệm trên đoạn $\left[-\dfrac{\pi}{2};\dfrac{\pi}{2}\right]$ là $x=-\dfrac{\pi}{6}$ và $x=\dfrac{\pi}{6}$
d) d) Giá trị nhỏ nhất của hàm số $y=f(x)$ trên đoạn $\left[-\dfrac{\pi}{2};\dfrac{\pi}{2}\right]$ là $-\dfrac{\pi}{2}$

Question 107. (Sở Tuyên Quang 2025) Cho hàm số $f(x)=\sin x+\cos x$.

a) a) Đạo hàm của hàm số đã cho là $f'(x)=\cos x-\sin x$
b) b) Giả sử $\sin x + \cos x = \dfrac{\sqrt{2}}{2}$ khi đó $\sin x.\cos x = \dfrac{1}{4}$
c) c) Giá trị lớn nhất của hàm số $f(x)$ trên đoạn $\left[0;\dfrac{3\pi}{4}\right]$ bằng $a\sqrt{b}$, với a,b là các số nguyên dương. Khi đó $b-a=2$
d) d) Tổng các nghiệm của phương trình $f'(x)=0$ trên khoảng $(0;3\pi)$ bằng $\dfrac{15\pi}{4}$

Question 108. (Sở Phú Thọ 2025) Cho hàm số $f(x)=2\sin x+\sqrt{3}x$.

a) a) $f(0)=0, f(\pi)=\sqrt{3}\pi$
b) b) Đạo hàm của hàm số đã cho là $f'(x)=-2\cos x+\sqrt{3}$
c) c) Nghiệm của phương trình $f'(x)=0$ trên đoạn $[0;\pi]$ là $\dfrac{\pi}{6}$
d) d) Giá trị lớn nhất của hàm số $f(x)$ trên đoạn $[0;\pi]$ bằng $1+\dfrac{5\sqrt{3}\pi}{6}$

Question 109. (Sở Bình Thuận 2025) Cho hàm số $f(x)=2\sin x\cos x+\sqrt{2}x$.

a) a) Hàm số đã cho liên tục trên đoạn $\left[-\dfrac{\pi}{3};\pi\right]$
b) b) Đạo hàm của hàm số đã cho là $f'(x)=2\cos 2x+\sqrt{2}$
c) c) Trên đoạn $\left[-\dfrac{\pi}{3};\pi\right]$, phương trình $f'(x)=0$ có đúng một nghiệm là $\dfrac{3\pi}{8}$
d) d) Giá trị nhỏ nhất của $f(x)$ trên đoạn $\left[-\dfrac{\pi}{3};\pi\right]$ là $\dfrac{\sqrt{3}}{2}+\dfrac{\pi\sqrt{2}}{3}$

Question 110. (THPT Triệu Quang Phục - Hưng Yên 2025) Cho đồ thị hàm số $y=\cos x/\left[-\dfrac{5\pi}{2};\dfrac{5\pi}{2}\right]$ dưới đây. Xét tính đúng sai của các phát biểu sau:

a) a) Hàm số đã cho đồng biến trên các khoảng $(-\pi;0)$ và $(\pi;2\pi)$
b) b) Giá trị lớn nhất, giá trị nhỏ nhất của hàm số là $Max y=1; Min y=-1$
c) c) Hàm số đã cho là hàm tuần hoàn với chu kì $2\pi$
d) d) Phương trình $\cos x=a$ với $0 True

Question 111. (THPT Hà Trung - Thanh Hóa 2025) Cho hai hàm số $f(x)=\sin x-x$ và $g(x)=\sin x - x + m^2+2m-3$. Gọi S là tập các giá trị của m để giá trị lớn nhất của hàm $y=g(x)$ trên đoạn $[0;\pi]$ bằng $-4$.

a) a) Tập S có hai phân tử
b) b) Nghiệm của phương trình $f'(x)=0$ là $x=\pi+k2\pi \ (k \in \mathbb{Z})$
c) c) $f\left(\dfrac{\pi}{2}\right)=1-\dfrac{\pi}{2}$
d) d) Hàm số $y=f(x)$ đồng biến trên tập xác định

Question 112. (THPT Phúc Thọ - Hà Nội 2025) Cho hàm số $y=f(x)=\sqrt{3}\tan 2x$

a) a. Phương trình $f(x)=3$ có nghiệm $x=\dfrac{\pi}{6}+k\dfrac{\pi}{2}, k \in \mathbb{Z}$
b) b) Tập xác định của hàm số là $D=\mathbb{R}\setminus\{\dfrac{\pi}{4}+k\pi, k \in \mathbb{Z}\}$
c) c) Hàm số $y=f(x)$ là hàm số chẵn
d) d) Trên đường tròn lượng giác có 4 điểm biểu diễn nghiệm của phương trình $f(x)=3$

Question 113. (Sở Lai Châu 2025) Cho hàm số $f(x)=x-\sin 2x$.

a) a) $f\left(-\dfrac{\pi}{2}\right)=-\dfrac{\pi}{2}, f(\pi)=\pi$
b) b) $f'(x)=1-\cos 2x$
c) c) Phương trình $f'(x)=0$ trên đoạn $\left[-\dfrac{\pi}{2};\pi\right]$ có tập nghiệm là $T=\left\{-\dfrac{\pi}{6};\dfrac{\pi}{6};\dfrac{5\pi}{6}\right\}$
d) d) Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn $\left[-\dfrac{\pi}{2};\pi\right]$ bằng $\dfrac{\pi}{3}+\dfrac{\sqrt{3}}{2}$

Question 114. (Cụm chuyên môn Đak Lak 2025) Cho hàm số $f(x)=2\sin x+1$.

a) a) Đạo hàm của hàm số đã cho là $f'(x)=2\cos x+1$
b) b) Giá trị nhỏ nhất của hàm số $f(x)$ là $-1$
c) c) Nghiệm của phương trình $f'(x)=0$ trên đoạn $\left[0;\dfrac{\pi}{2}\right]$ là $\dfrac{\pi}{4}$
d) d) $f(0)=1; f\left(\dfrac{\pi}{2}\right)=3$

Question 115. (Liên trường THPT Ninh Bình 2025) Cho hàm số $f(x)=\sin 2x+x$

a) a) Giá trị lớn nhất của $f(x)$ trên đoạn $[0;\pi]$ là $\pi$
b) b) Trên đoạn $[0;\pi]$, phương trình $f'(x)=0$ có đúng hai nghiệm là $\dfrac{\pi}{3}$ và $\dfrac{2\pi}{3}$
c) c) $f(0)=0; f(\pi)=\pi$
d) d) Đạo hàm của hàm số đã cho là $f'(x)=\cos 2x+1$

Question 116. (THPT Nông Cống 3 - Thanh Hóa 2025) Cho hàm số $f(x)=\sin^2 x+\cos x-1$. Khi đó

a) a) Nghiệm dương bé nhất của phương trình $f(x)=0$ là $\dfrac{\pi}{2}$
b) b) $f'(x)=2\sin x-\sin x$
c) c) Gọi giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y=f(x)$ trên $\left[\dfrac{\pi}{2};\dfrac{3\pi}{4}\right]$ lần lượt là M, m. Khi đó $M+m=\dfrac{-1-2\sqrt{2}}{4}$
d) d) $f(-\pi)=-f(\pi)$

Question 117. (THPT Lê Hồng Phong - Hải Phòng 2025) Cho hàm số $f(x) = 2\cos x+x\sqrt{2}$.

a) a) Đạo hàm của hàm số đã cho là $f'(x) = 2\sin x+\sqrt{2}$
b) b) $f(0)=2; f(\pi)=-2+\pi\sqrt{2}$
c) c) Tổng giá trị lớn nhất và giá trị nhỏ nhất của $f(x)$ trên đoạn $[0;\pi]$ là $\pi\sqrt{2}$
d) d) Phương trình $f'(x)=0$ có đúng hai nghiệm trên đoạn $[0;\pi]$

Question 118. (Sở Quảng Bình 2025) Cho hàm số $f(x)=\sin 2x-x$.

a) a) $f\left(-\dfrac{\pi}{2}\right) = \dfrac{\pi}{2}; f\left(\dfrac{\pi}{2}\right)=-\dfrac{\pi}{2}$
b) b) Đạo hàm của hàm số đã cho là $f'(x)=\cos 2x-1$
c) c) Phương trình $f'(x)=0$ có hai nghiệm trên đoạn $\left[-\dfrac{\pi}{2};\dfrac{\pi}{2}\right]$ là $x=-\dfrac{\pi}{6}$ và $x=\dfrac{\pi}{6}$
d) d) Giá trị nhỏ nhất của hàm số $y=f(x)$ trên đoạn $\left[-\dfrac{\pi}{2};\dfrac{\pi}{2}\right]$ là $-\dfrac{\pi}{2}$

Question 119. (Sở Tuyên Quang 2025) Cho hàm số $f(x)=\sin x+\cos x$.

a) a) Đạo hàm của hàm số đã cho là $f'(x)=\cos x-\sin x$
b) b) Giả sử $\sin x + \cos x = \dfrac{\sqrt{2}}{2}$ khi đó $\sin x.\cos x = \dfrac{1}{4}$
c) c) Giá trị lớn nhất của hàm số $f(x)$ trên đoạn $\left[0;\dfrac{3\pi}{4}\right]$ bằng $a\sqrt{b}$, với a,b là các số nguyên dương. Khi đó $b-a=2$
d) d) Tổng các nghiệm của phương trình $f'(x)=0$ trên khoảng $(0;3\pi)$ bằng $\dfrac{15\pi}{4}$

Question 120. (Sở Phú Thọ 2025) Cho hàm số $f(x)=2\sin x+\sqrt{3}x$.

a) a) $f(0)=0, f(\pi)=\sqrt{3}\pi$
b) b) Đạo hàm của hàm số đã cho là $f'(x)=-2\cos x+\sqrt{3}$
c) c) Nghiệm của phương trình $f'(x)=0$ trên đoạn $[0;\pi]$ là $\dfrac{\pi}{6}$
d) d) Giá trị lớn nhất của hàm số $f(x)$ trên đoạn $[0;\pi]$ bằng $1+\dfrac{5\sqrt{3}\pi}{6}$

Question 121. (Sở Bình Thuận 2025) Cho hàm số $f(x)=2\sin x\cos x+\sqrt{2}x$.

a) a) Hàm số đã cho liên tục trên đoạn $\left[-\dfrac{\pi}{3};\pi\right]$
b) b) Đạo hàm của hàm số đã cho là $f'(x)=2\cos 2x+\sqrt{2}$
c) c) Trên đoạn $\left[-\dfrac{\pi}{3};\pi\right]$, phương trình $f'(x)=0$ có đúng một nghiệm là $\dfrac{3\pi}{8}$
d) d) Giá trị nhỏ nhất của $f(x)$ trên đoạn $\left[-\dfrac{\pi}{3};\pi\right]$ là $\dfrac{\sqrt{3}}{2}+\dfrac{\pi\sqrt{2}}{3}$

Question 122. (THPT Triệu Quang Phục - Hưng Yên 2025) Cho đồ thị hàm số $y=\cos x/\left[-\dfrac{5\pi}{2};\dfrac{5\pi}{2}\right]$ dưới đây. Xét tính đúng sai của các phát biểu sau:

a) a) Hàm số đã cho đồng biến trên các khoảng $(-\pi;0)$ và $(\pi;2\pi)$
b) b) Giá trị lớn nhất, giá trị nhỏ nhất của hàm số là $Max y=1; Min y=-1$
c) c) Hàm số đã cho là hàm tuần hoàn với chu kì $2\pi$
d) d) Phương trình $\cos x=a$ với $0 True

Question 123. (THPT Hà Trung - Thanh Hóa 2025) Cho hai hàm số $f(x)=\sin x-x$ và $g(x)=\sin x - x + m^2+2m-3$. Gọi S là tập các giá trị của m để giá trị lớn nhất của hàm $y=g(x)$ trên đoạn $[0;\pi]$ bằng $-4$.

a) a) Tập S có hai phân tử
b) b) Nghiệm của phương trình $f'(x)=0$ là $x=\pi+k2\pi \ (k \in \mathbb{Z})$
c) c) $f\left(\dfrac{\pi}{2}\right)=1-\dfrac{\pi}{2}$
d) d) Hàm số $y=f(x)$ đồng biến trên tập xác định

Question 124. (THPT Phúc Thọ - Hà Nội 2025) Cho hàm số $y=f(x)=\sqrt{3}\tan 2x$

a) a. Phương trình $f(x)=3$ có nghiệm $x=\dfrac{\pi}{6}+k\dfrac{\pi}{2}, k \in \mathbb{Z}$
b) b) Tập xác định của hàm số là $D=\mathbb{R}\setminus\{\dfrac{\pi}{4}+k\pi, k \in \mathbb{Z}\}$
c) c) Hàm số $y=f(x)$ là hàm số chẵn
d) d) Trên đường tròn lượng giác có 4 điểm biểu diễn nghiệm của phương trình $f(x)=3$

Question 125. (Sở Lai Châu 2025) Cho hàm số $f(x)=x-\sin 2x$.

a) a) $f\left(-\dfrac{\pi}{2}\right)=-\dfrac{\pi}{2}, f(\pi)=\pi$
b) b) $f'(x)=1-\cos 2x$
c) c) Phương trình $f'(x)=0$ trên đoạn $\left[-\dfrac{\pi}{2};\pi\right]$ có tập nghiệm là $T=\left\{-\dfrac{\pi}{6};\dfrac{\pi}{6};\dfrac{5\pi}{6}\right\}$
d) d) Tổng giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn $\left[-\dfrac{\pi}{2};\pi\right]$ bằng $\dfrac{\pi}{3}+\dfrac{\sqrt{3}}{2}$

Question 126. (Cụm chuyên môn Đak Lak 2025) Cho hàm số $f(x)=2\sin x+1$.

a) a) Đạo hàm của hàm số đã cho là $f'(x)=2\cos x+1$
b) b) Giá trị nhỏ nhất của hàm số $f(x)$ là $-1$
c) c) Nghiệm của phương trình $f'(x)=0$ trên đoạn $\left[0;\dfrac{\pi}{2}\right]$ là $\dfrac{\pi}{4}$
d) d) $f(0)=1; f\left(\dfrac{\pi}{2}\right)=3$

Question 127. (Liên trường THPT Ninh Bình 2025) Cho hàm số $f(x)=\sin 2x+x$

a) a) Giá trị lớn nhất của $f(x)$ trên đoạn $[0;\pi]$ là $\pi$
b) b) Trên đoạn $[0;\pi]$, phương trình $f'(x)=0$ có đúng hai nghiệm là $\dfrac{\pi}{3}$ và $\dfrac{2\pi}{3}$
c) c) $f(0)=0; f(\pi)=\pi$
d) d) Đạo hàm của hàm số đã cho là $f'(x)=\cos 2x+1$

📋 Danh sách slide