Question 1. (THPT Lương Tài 2 - Bắc Ninh 2025) Cho hàm số $y = x^3 +9x^2-12$ có đồ thị là đường cong (C). Điểm $M(a;b)$ là điểm cực đại của đồ thị (C). Giá trị của $a-b$ bằng bao nhiêu?

Question 2. (THPT Lương Tài 2 - Bắc Ninh 2025) Cho hàm số $y = \dfrac{3x-3}{\sqrt{x^2-1}}$. Gọi a là số đường tiệm cận đứng và b là số đường tiệm cận ngang của đồ thị hàm số đã cho. Giá trị $20a+10b^2$ bằng bao nhiêu?

Question 3. (THPT Văn Giang - Hưng Yên 2025) Có bao nhiêu giá trị nguyên của tham số $m$ thuộc đoạn $[-2024; 2024]$ để hàm số $y = \dfrac{\sin x + m}{\sin x-1}$ nghịch biến trên khoảng $\left(\dfrac{\pi}{2}; \pi\right)$?

Question 4. (THPT Chuyên Vĩnh Phúc 2025) Cho hàm số $f(x)=x(x-3)^2$. Tính số nghiệm thực của phương trình $\underbrace{f(f\dots f(x))}_{8 \text{ lần } f} = 0$?

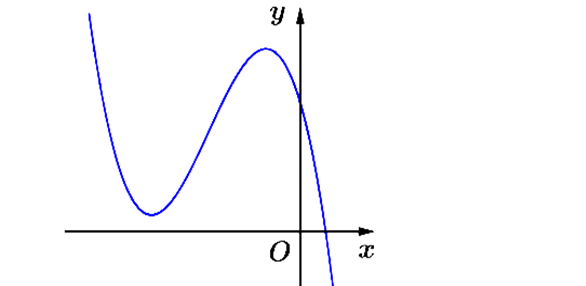
Question 5. (THPT Diễn Châu 5 - Nghệ An 2025) Cho hàm số $y = ax^3 +bx^2 +cx+d(a,b,c,d \in \mathbb{R})$ có đồ thị là đường cong trong hình bên. Có bao nhiêu số dương trong các số $a, b, c, d$?

Question 6. (THPT Triệu Sơn 3 - Thanh Hóa 2025) Cho hàm số $y = \dfrac{x^2+3x+3}{x+1}$ có đồ thị (C). Gọi $d$ là khoảng cách giữa hai điểm cực trị của (C) và $d_1$ là khoảng cách từ điểm cực đại của (C) đến gốc tọa độ. Giá trị của $d^2 + d_1^2$ bằng bao nhiêu?

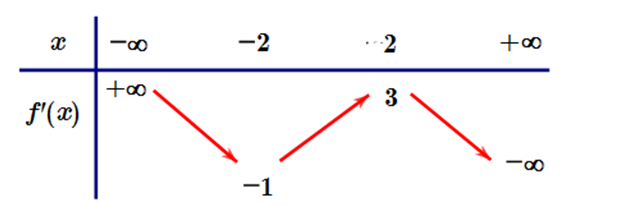
Question 7. (THPT Triệu Sơn 4 - Thanh Hóa 2025) Cho hàm số $y = f(x)$ có đạo hàm liên tục trên $\mathbb{R}$ và có bảng biến thiên của đạo hàm như hình vẽ. Đặt $g(x) = f\left(\dfrac{x^2+1}{x}\right)$. Tìm số điểm cực trị của hàm số $y = g(x)$.

Question 8. (Chuyên Phan Bội Châu - Nghệ An 2025) Hàm số $y= \dfrac{x^2-x+1}{x-1}$ có giá trị cực đại và giá trị cực tiểu lần lượt là $a$ và $b$. Tính $3a+2b$.

Question 9. (THPT Lê Xoay - Vĩnh Phúc 2025) Cho hàm số $y = f(x)= \dfrac{2x^2 +26x+18}{x+13}$ có điểm cực tiểu $x = x_1$ và điểm cực đại $x = x_2$. Tính $P = -2x_1 + x_2$.

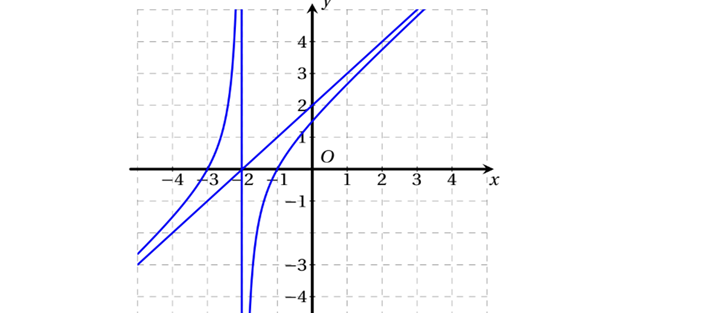
Question 10. (Cụm trường THPT Bắc Ninh 2025) Trong hệ trục tọa độ (Oxy) cho đồ thị hàm số (C): $y = \dfrac{x^2+x+1}{x+1}$ mô tả chuyển động của hai tàu đánh cá $A$ và $B$ (đơn vị trên mỗi trục tọa độ tính bằng km). Biết quỹ đạo chuyển động của hai tàu luôn thuộc về hai nhánh khác nhau của đồ thị (C). Tính khoảng cách ngắn nhất (đơn vị km) giữa hai tàu đánh cá $A$ và $B$ (kết quả làm tròn đến hàng phần trăm).

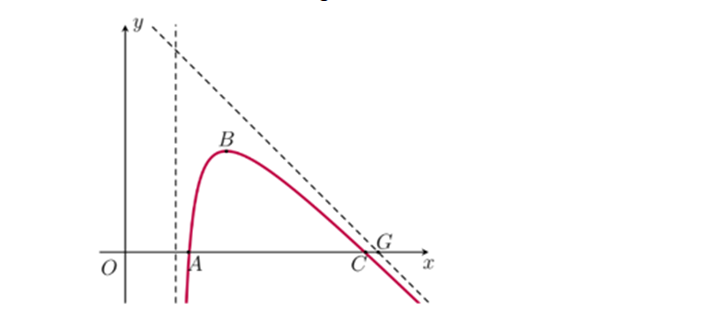
Question 11. (Sở Hà Tĩnh 2025) Một máy bay trình diễn có đường bay gắn với hệ trục $Oxy$ được mô phỏng như hình vẽ, trục $Ox$ gắn với mặt đất. Đường bay có dạng là một phần của đồ thị hàm phân thức bậc hai trên bậc nhất $y = f(x)$ có đường tiệm cận đứng là $x = 2$. Điểm $G$ là giao điểm của đường tiệm cận xiên của đồ thị hàm số $y = f(x)$ và trục $Ox$ được gọi là điểm giới hạn. Biết máy bay bay từ vị trí $A$ cách tọa tọa độ $O$ một khoảng 2,5 đơn vị và máy bay khi ở vị trí cao nhất cách điểm xuất phát 1,5 đơn vị theo phương song song với trục $Ox$ và cách mặt đất 4,5 đơn vị. Vị trí máy bay tiếp đất cách điểm giới hạn một khoảng bằng bao nhiêu?

Question 12. (Chuyên Hạ Long 2025) Tính giá trị cực tiểu của hàm số $y = x^4 - 3x^2 +1$.

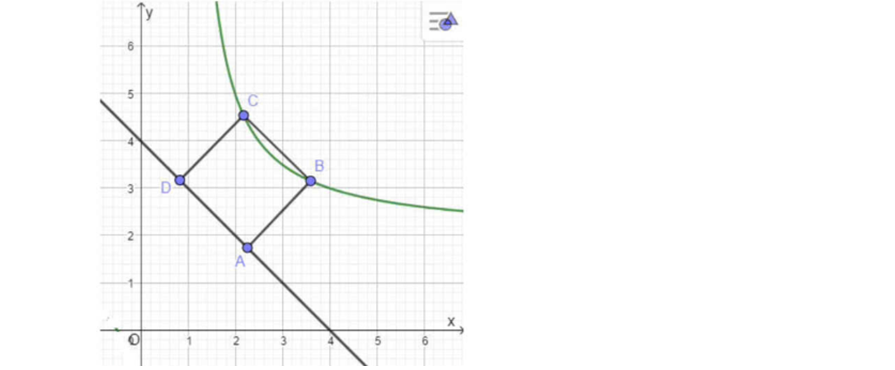
Question 13. (Chuyên Hạ Long 2025) Trong một công viên có một hồ nước và một đường đi lát gạch hoa. Thiết lập hệ trục $Oxy$ như hình vẽ dưới, kiến trúc sư thấy rằng bờ hồ có thể coi như một nhánh của đồ thị hàm số $y = \dfrac{2x+1}{x-1}$ và đường đi khi đó ứng với đường thẳng $(d): y = -x+4$. Để đảm bảo ánh sáng, kiến trúc sư muốn đặt 2 cột đèn trên bờ hồ và 2 cột đèn trên đường đi sao cho 4 cột đèn này tạo thành một hình vuông. Tính khoảng cách giữa hai cột đèn trên bờ hồ (làm tròn đến hàng phần trăm).

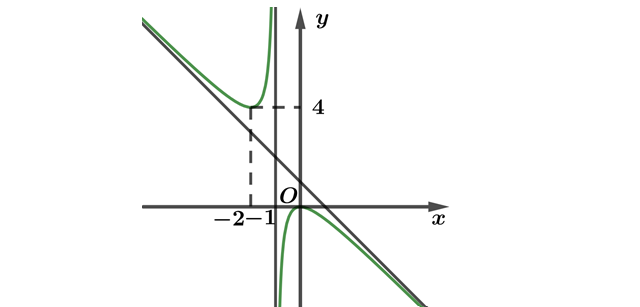
Question 14. (Chuyên Thái Bình 2025) Cho hàm số $y = \dfrac{ax^2 + bx + c}{x+d}$ có đồ thị như hình vẽ dưới đây. Tính $a+b+c+d$.

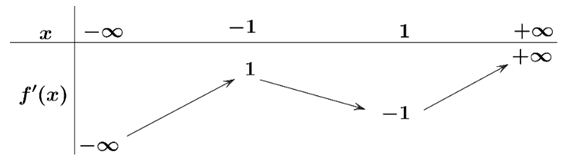
Question 15. (Chuyên Thái Bình 2025) Cho hàm số $y = f(x)$ liên tục trên $\mathbb{R}$. Hàm số $y = f'(x)$ có bảng biến thiên như hình vẽ dưới. Tìm số điểm cực trị của hàm số $g(x) = f(2x)-x$.

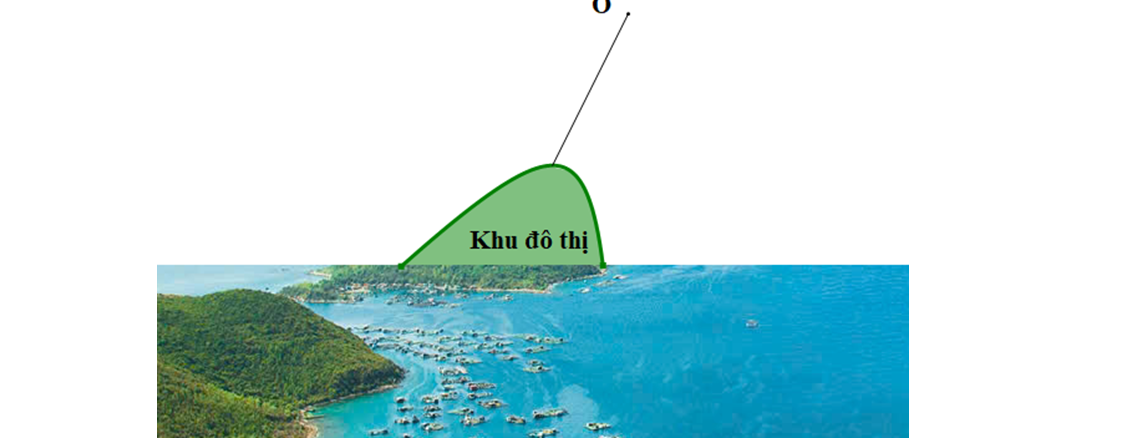
Question 16. (Chuyên Vinh 2025) Ở một vịnh biển, ngoài xa có một hòn đảo nhỏ. Người ta tiến hành lấn biển để xây một khu đô thị và làm một tuyến cáp treo nối khu đô thị với hòn đảo để phát triển du lịch. Xét trong hệ tọa độ $Oxy$ với đơn vị đo tương ứng 1km có hòn đảo ở $O$ thì đương bao của phần đất lấn biển có dạng là một phần của đồ thị hàm số $y = \dfrac{x^2 +1}{x}$. Giả sử tuyến cáp treo được thiết kế nối đảo với đường bao của khu đô thị với độ dài ngắn nhất. Độ dài của tuyến cáp treo là bao nhiêu km (làm tròn kết quả đến hàng phần mười)?

Question 17. (Cụm trường Hải Dương 2025) Cho hàm số $y = \dfrac{x^2-2x+2}{x-1}$ có đồ thị là (C). Gọi $I$ là giao điểm của hai đường tiệm cận của đồ thị (C). Trên đồ thị (C) có một điểm $M(a;b)$ với $a > 1$ sao cho khoảng cách $IM$ là nhỏ nhất. Tìm $a$ (làm tròn kết quả đến hàng phần trăm).

Question 18. (THPT Sào Nam - Quảng Nam 2025) Cho hàm số $y = f(x) = \dfrac{ax^2 + bx +3}{x+c}$ với $a \ne 0$, có đồ thị là đường cong như hình vẽ bên dưới Giá trị $S = a+b+c$ là bao nhiêu?

Question 19. (THPT Trực Ninh - Nam Định 2025) Biết đồ thị hàm số $y = x^3 + 3x^2 -9x-1$ có hai cực trị $A$ và $B$. Phương trình đường thẳng $AB$ là $y = ax+b(a,b\in\mathbb{R})$. Tính tổng $a + b$.

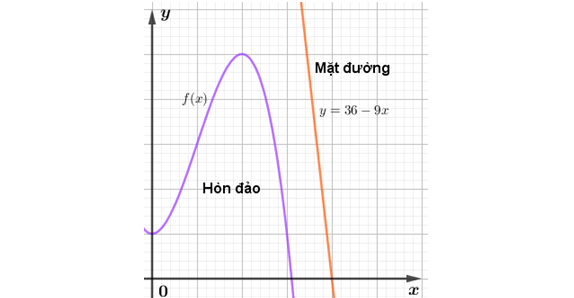
Question 20. (THPT Trực Ninh - Nam Định 2025) Một hòn đảo nằm trong một hồ nước. Biết rằng đường cong tạo nên hòn đảo được mô hình hóa vào hệ trục tọa độ $Oxy$ là một phần của đồ thị hàm số bậc ba $f(x)$. Vị trí điểm cực đại là $(2;5)$ với đơn vị của hệ trục là 100m và vị trí điểm cực tiểu là $(0;1)$. Mặt đường chạy trên một đường thẳng có phương trình $y = 36-9x$. Người ta muốn làm một cây cầu có dạng một đoạn thẳng nối từ hòn đảo ra mặt đường. Độ dài ngắn nhất của cây cầu bằng bao nhiêu mét? (làm tròn đến hàng phần chục)

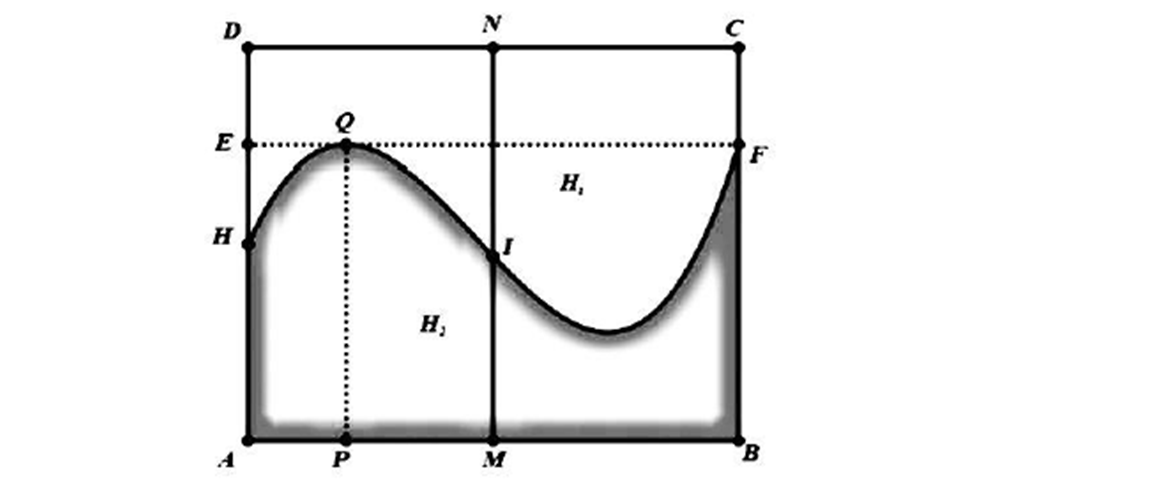
Question 21. (Sở Ninh Bình 2025) Khuôn viên của một công viên có dạng hình chữ nhật $ABCD$ với $AB = 100\,\text{m}; AD = 80\,\text{m}$. Người ta muốn chia công viên thành hai khu, một khu dành cho trẻ em, một khu dành cho người lớn. Để tạo thiết kế độc đáo và lạ mắt, người ta dùng một đường cong chia khuôn viên thành hai phần $H_1$ (không tô màu) dành cho trẻ em và $H_2$ (tô màu) dành cho người lớn như hình vẽ bên với $AH = 40\,\text{m}; AE = 60\,\text{m}; AP = 20\,\text{m}$ và $EF //AB; PQ//AD$. Biết rằng khi xét trong một hệ tọa độ $Oxy$, đường cong trong hình là một phần của đồ thị hàm số bậc ba. Phần chính giữa công viên người ta muốn mắc dây đèn trang trí dọc đoạn thẳng $MN$ như hình. Biết giá tiền mỗi mét dây trang trí của phần dành cho trẻ em là 140 nghìn đồng và phần dành cho người lớn là 180 nghìn đồng. Tổng số tiền mắc dây đèn trang trí trên đoạn $MN$ là bao nhiêu triệu đồng.

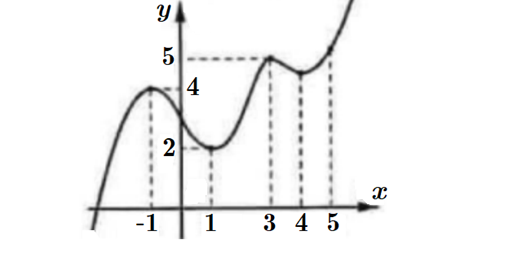
Question 22. (THPT Nông Cống 3 - Thanh Hóa 2025) Cho hàm số $y = f(x)$ liên tục trên $\mathbb{R}$ và có đồ thị như hình vẽ. Gọi $M,m$ lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số $h(x) = 3f(\log_2 x-1)+x^3 -9x^2 +15x+1$ trên đoạn $[1;4]$. Tính giá trị của biểu thức $T = M+m$.

Question 23. (Sở Hà Nội 2025) Đồ thị hàm số $y = \dfrac{x^2}{x+1}$ có hai điểm cực trị $A$ và $B$. Độ dài đoạn thẳng $AB$ bằng bao nhiêu (kết quả làm tròn đến hàng phần chục)?

Question 24. (Sở Yên Bái 2025) Gọi $M(a;b)$ là điểm thuộc đồ thị hàm số $y = \dfrac{2x+1}{x+2}$ và có khoảng cách từ $M$ đến đường thẳng $d: y = 3x +6$ nhỏ nhất. Tính giá trị của biểu thức $T = 6a^2 +7b^2$.

Question 25. (Sở Đà Nẵng 2025) Một giáo viên theo dõi sự tiến bộ của học sinh qua thang đo điểm, được mô hình hoá bằng hàm số $f(x)=x^3+ax^2+bx+c$ với $a,b,c$ là các hệ số. Trong đó, $x$ ($0 \le x \le 9, x \in \mathbb{N}$) là số tháng kể từ đầu năm học và $f(x)$ là điểm trong tháng thứ $x$. Qua theo dõi, giáo viên ghi nhận tháng đầu tiên học sinh đạt 19 điểm, sau đó giảm trong tháng thứ hai và đến tháng thứ ba học sinh đạt mức điểm thấp nhất trong năm học, là 3 điểm. Kể từ tháng thứ ba trở đi, điểm của học sinh tăng lên. Tính điểm của học sinh đó ở tháng thứ sáu.

Question 26. (Sở Quảng Nam 2025) Biết đồ thị hàm số $y = \dfrac{x^2-4x+5}{x-2}$ có điểm cực tiểu là $M(x_0;y_0)$, tính $T = x_0 + y_0$.

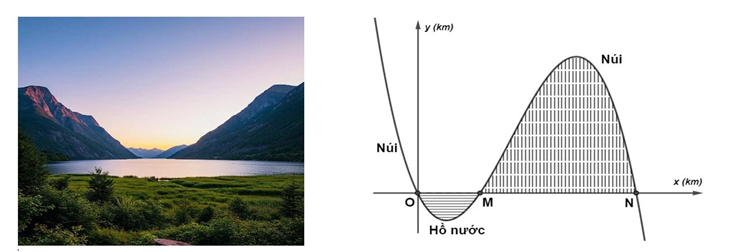
Question 27. (THPT Ngô Sĩ Liên - Bắc Giang 2025) Lát cắt của một vùng đất được mô hình hóa bởi hàm bậc ba $y = f(x)$ có đồ thị như hình vẽ dưới (đơn vị trên các trục là km). Biết khoảng cách $OM = 2\text{km}$; độ rộng của núi $MN = 3,5\text{km}$. Độ sâu của hồ nước là 450m. Chiều cao của ngọn núi là bao nhiêu mét? (làm tròn đến hàng đơn vị).

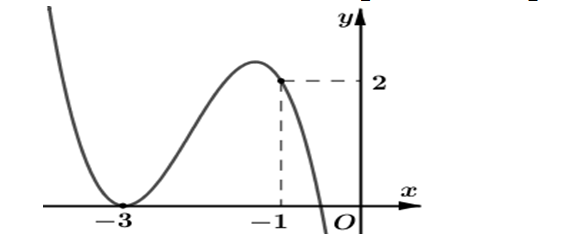
Question 28. (THPT Hoằng Hóa 2-Thanh Hóa 2025) Cho hàm bậc ba $y = f(x)$ có đồ thị như hình vẽ bên. Hỏi đồ thị hàm số $y = \dfrac{(x^2+4x+3)\sqrt{x^2+x}}{x[f^2(x)-2f(x)]}$ có bao nhiêu đường tiệm cận đứng?

Question 29. (THPT Tư Nghĩa 1 - Quảng Ngãi 2025) Tính giá trị nhỏ nhất của hàm số $y = 3x + \dfrac{4}{x^2}$ trên khoảng $(0;+\infty)$. (Quy tròn đến hàng phần trăm)

Question 30. (THPT Quế Võ 1 - Bắc Ninh 2025) Gọi $M,m$ lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số $y = \dfrac{3\sin x + 2}{\sin x + 1}$ trên đoạn $\left[0; \dfrac{\pi}{2}\right]$. Khi đó giá trị của $M^2 + m^2 = \dfrac{b}{c}$, tính $T=b-c$.

Question 31. (THPT Triệu Quang Phục - Hưng Yên 2025) Hàm số $y = x^3 + ax^2 + bx +2$ đạt cực tiểu tại $x = 1$. Tính tổng $b+2a$.

Question 32. (THPT Triệu Quang Phục - Hưng Yên 2025) Cho các hàm số $f(x) = x^2 - 4x+m$, với $m$ là tham số và $g(x) = (x^2+1)(x^2+2)^2 (x^2 +3)^3$. Tìm số giá trị nguyên của $m\in [3;10]$ để hàm số $g(f(x))$ đồng biến trên khoảng $(3;+\infty)$.

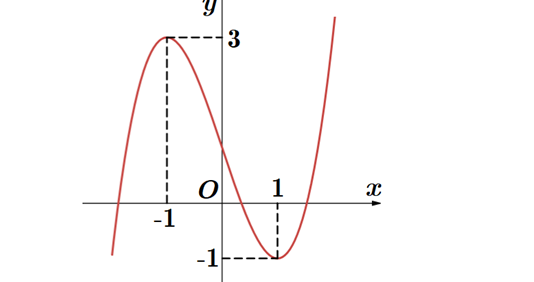
Question 33. (THPT Triệu Quang Phục - Hưng Yên 2025) Cho hàm số $y = f(x)$ có đồ thị như hình bên dưới. Có tất cả bao nhiêu già trị nguyên dương của tham số $m$ để phương trình $25^{f(x)} +125m = m \cdot 5^{f(x)} + 5^{f(x)+3}$ có đúng 5 nghiệm thực phân biệt?

Question 34. (Cụm Chuyên Môn Đăk Lak 2025) Cho hàm số $y = x^3 - 3x$, có giá trị cực đại và cực tiểu lần lượt là $y_1$ và $y_2$. Khi đó giá trị của biểu thức $2y_1 - y_2$ bằng bao nhiêu?

Question 35. (THPT Hà Trung - Thanh Hóa 2025) Có bao nhiêu giá trị nguyên của tham số $m$ thuộc $(-2025;2025)$ để hàm số $y = \dfrac{m\log_2 x-2}{\log_2 x-m-1}$ nghịch biến trên $(4;+\infty)$.

Question 36. (Sở Bắc Ninh 2025) Cho hàm số $f(x) = \dfrac{\sqrt{ax^2+1}-bx-2}{-x^3+3x-2}$ (với $a, b$ là các hằng số). Biết rằng $f(x)$ liên tục tại điểm $x = 1$. Giá trị của $f(1)$ bằng bao nhiêu?

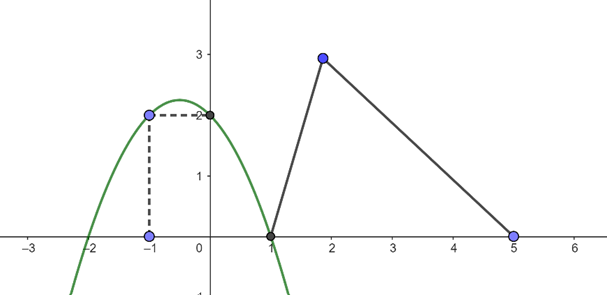
Question 37. (THPT Phúc Thọ - Hà Nội 2025) Cho hàm số $f(x)$. Đồ thị hàm số $f'(x)$ trên $[-2;5]$ như hình vẽ (Phần cong là phần của Parabol $y = ax^2+bx+c$). Biết $f(-2)=0$, giá trị của $f(1)+f(3)$ bằng bao nhiêu?

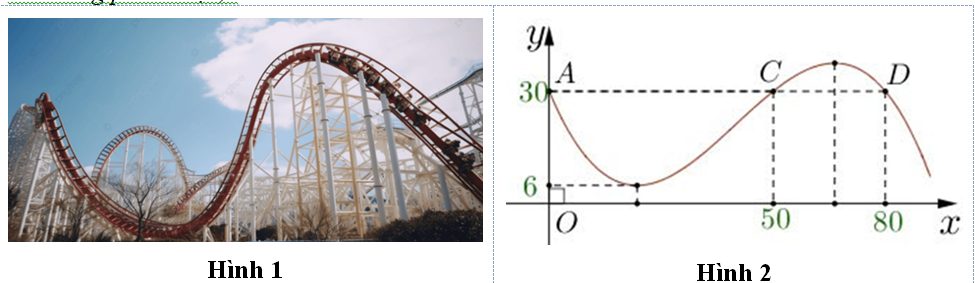
Question 38. (THPT Lê Quý Đôn - Hà Nội 2025) Một phần đường chạy của tàu lượn siêu tốc (hình 1) khi gắn hệ trục toạ độ $Oxy$ được mô phỏng ở hình 2, đơn vị trên mỗi trục là mét. Biết đường chạy của nó là một phần đồ thị hàm bậc ba $y=ax^3+bx^2+cx+d(0 \le x < 90)$; tàu lượn siêu tốc xuất phát từ điểm $A$, đi qua các điểm $C,D$ đồng thời đạt độ cao nhỏ nhất so với mặt đất là 6m. Độ cao lớn nhất mà tàu lượn siêu tốc đạt được là bao nhiêu mét so với mặt đất? (Kết quả làm tròn đến hàng phần chục).

Question 39. (THPT Nguyễn Quốc Trinh - Hà Nội 2025) Cho hàm số $y = \dfrac{x^2+3x+3}{x+1}$ có đồ thị (C). Gọi $d_1$ là khoảng cách giữa hai điểm cực trị của (C) và $d_2$ là khoảng cách từ điểm cực tiểu của (C) đến gốc tọa độ. Giá trị của $d_1^2 + 2d_2^2$ bằng bao nhiêu?

Question 40. (Chuyên Lam Sơn - Thanh Hóa 2025) Cho hàm số $y = \dfrac{x^2-2x-2}{x+1}$ có đồ thị (C). Gọi $A, B$ là hai điểm cực trị của đồ thị (C). Tính bình phương của độ dài đoạn thẳng $AB$.

Question 41. (THPT Cụm trường Hải Dương 2025) Lát cắt của một vùng đất được mô hình hóa là một phần hàm số bậc ba $y = f(x)$ có đồ thị như hình vẽ (đơn vị độ dài trên các trục là kilômét). Biết khoảng cách hai bên chân đồi $OM = 2(\text{km})$, độ rộng của hồ nước $MN =1(\text{km})$ và ngọn đồi cao $528(\text{m})$. Độ sâu nhất của hồ nước là bao nhiêu mét? (làm tròn kết quả đến hàng đơn vị của mét)