Question 206. Trong không gian Oxyz, cho $\vec{OA} = 3\vec{i} + 4\vec{j} - 5\vec{k}$. Tọa độ điểm $A(x;y;z)$. Giá trị biểu thức $S = 100x+1000y+10z$ bằng bao nhiêu?

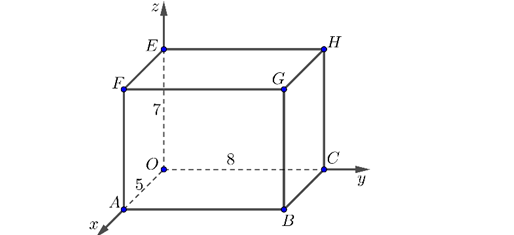
Question 207. Trong không gian Oxyz cho hình hộp chữ nhật OABC.EFGH có các cạnh OA = 5, OC = 8, OE = 7 (xem hình vẽ dưới đây). Tọa độ $H(x;y;z)$. Tính giá trị biểu thức $P = 50x + 75y +1000z$

Question 208. Trong không gian Oxyz, cho hai điểm $A(4;2;1), B(-2;-1;4)$. Gọi M là điểm thỏa mãn đẳng thức $\vec{AM} = 2\vec{MB}$. Tìm độ dài vectơ $\vec{OM}$.

Question 209. Trong không gian Oxyz, cho $A(3;2;-1), B(-1;0;5)$. Điểm $M(a;b;c)$ thay đổi thuộc mặt phẳng (Oxy). Tính giá trị của biểu thức $T =a+b+c$ khi $|\vec{MA} + \vec{MB}|$ nhỏ nhất.

Question 210. Trong không gian Oxyz cho $A(1;0;2), B(-1;2;2), C(3;1;1)$. Gọi $M(a;b;c)$ là điểm thuộc mặt phẳng (Oxz) sao cho biểu thức $S = 2\vec{MA}.\vec{MB}+\vec{MB}.\vec{MC}+3\vec{MC}.\vec{MA}$ đạt giá trị nhỏ nhất. Khi đó $T = 6a-5b+3c$ có giá trị là

Question 211. Trong không gian Oxyz, cho hình hộp $ABCD.A'B'C'D'$ có $A(0;0;0), B(3;0;0), D(0;3;0), D'(0;3;-3)$. Gọi G là trọng tâm tam giác A'B'C và tọa độ vecto $\vec{AG} = (a;b;c)$. Tính $S=a+b+c$.

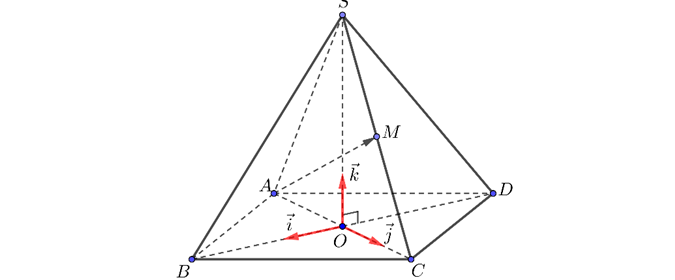
Question 212. Trong không gian Oxyz, cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh bằng 5, giao điểm hai đường chéo AC và BD trùng với gốc O. Các vectơ $\vec{OB}, \vec{OC}, \vec{OS}$ lần lượt cùng hướng với $\vec{i}, \vec{j}, \vec{k}$ và $OA = OS=4$ như hình bên dưới. Toạ độ vectơ $\vec{AM} = (a;b;c)$ với M là trung điểm của cạnh SC, khi đó $a+b+c$ bằng bao nhiêu?

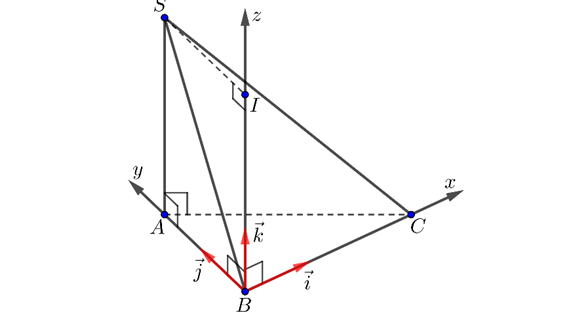
Question 213. Cho tứ diện SABC có ABC là tam giác vuông tại B, $BC = 3, BA = 2, SA$ vuông góc với mặt phẳng (ABC) và có độ dài bằng 2. Chọn hệ trục tọa độ như hình bên dưới. Điểm $D(a;b;c)$ sao cho SBCD là hình bình hành. Khi đó $a+b+c$ bằng bao nhiêu?

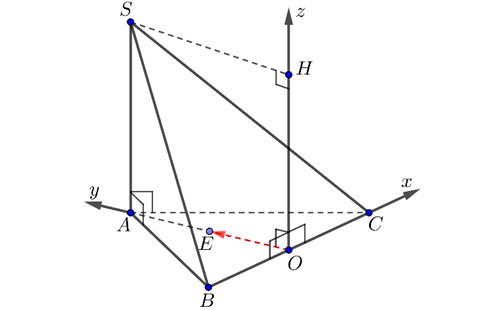
Question 214. Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng 2, SA vuông góc với đáy và SA bằng 1. Thiết lập hệ tọa độ như hình vẽ bên dưới, tọa độ điểm $S(a;\sqrt{b};c)$. Khi đó $a+b+c$ bằng bao nhiêu?

Question 215. Trong không gian với một hệ trục toạ độ cho trước (đơn vị đo lấy theo kilômét), ra đa phát hiện một chiếc máy bay di chuyển với vận tốc và hướng không đổi từ điểm $A(800;500;7)$ đến điểm $B(940;550;9)$ trong 10 phút. Nếu máy bay tiếp tục giữ nguyên vận tốc và hướng bay thì toạ độ của máy bay sau 5 phút tiếp theo là $C(x;y;z)$. Tính $x+y+z$.

Question 216. Trong không gian Oxyz, cho hình hộp $OABC.O'A'B'C'$ và các điểm $A(2;3;1), C(-1;2;3)$ và $O'(1;-2;2)$. Vecto $\vec{d} = \vec{OB}+\vec{OC}+\vec{OA'}+\vec{OB'}$ có tọa độ là $(a;b;c)$. Tính $a+b+c$.

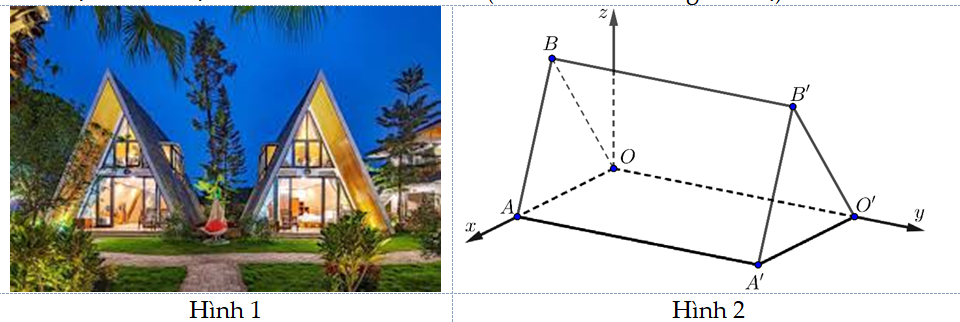
Question 217. Những căn nhà gỗ trong Hình 1 được phác thảo dưới dạng một hình lăng trụ đứng tam giác $OAB.O'A'B'$ như trong Hình 2. Với hệ trục toạ độ Oxyz thể hiện như Hình 2 (đơn vị đo lấy theo centimét), hai điểm A' và B' có tọa độ lần lượt là (240;450;0) và (120;450;300). Mỗi căn nhà gỗ có chiều dài là a cm, chiều rộng là bcm, mỗi cạnh bên của mặt tiền có độ dài là ccm. Tính $a+b+c$ (Làm tròn đến hàng đơn vị).

Question 218. Trong không gian với hệ tọa độ Oxyz, cho các điểm $\vec{OA}=\vec{i}+0\vec{j}+3\vec{k}, \vec{OB}=2\vec{i}+3\vec{j}-4\vec{k}, \vec{OC} = -3\vec{i} + \vec{j} + 2\vec{k}$. Điểm $D(x;y;z)$ sao cho ABCD là hình bình hành. Tính $P = 2x + y - z$.

Question 219. Trong không gian với hệ tọa độ Oxyz, cho $\vec{a}=2\vec{i}+3\vec{k}; \vec{b}=3\vec{i}+3\vec{j}$. Tọa độ vec tơ $\vec{a}=(x;0;3); \vec{b}=(3;y;0)$. Tính $P = x^2 + y^2$.

Question 220. Trong không gian với hệ tọa độ Oxyz, cho $\vec{OM}=2\vec{i}-3\vec{j}+4\vec{k}; \vec{ON}=-\vec{i}+3\vec{j}-\vec{k}$. Tọa độ điểm $M(2;-3;a); N(-1;b;-1)$. Tính $T = 2a - 3b$.

Question 221. Trong không gian với hệ tọa độ Oxyz,cho $\vec{a} = (3;-5;2); \vec{b} = (2;1;-1)$. Vecto $\vec{a}=3\vec{i}-y\vec{j}+2\vec{k}; \vec{b}=2\vec{i}+\vec{j}+z\vec{k}$. Tính $P = y^2-z^2$.

Question 222. Trong không gian với hệ tọa độ Oxyz, $M(1;0;-2), N(5;1;-6)$. Tính $\vec{OM}=\vec{i}+y\vec{j}-2\vec{k}; \vec{ON}=x\vec{i}+\vec{j}-6\vec{k}$. Tính $P=x^3+y^3$.

Question 223. Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng 5, $SA = 2$ và $SA \perp (ABCD)$. Chọn hệ trục Oxyz có gốc toạ độ tại A; các điểm B, D, S lần lượt trên các tia Ox, Oy, Oz. Tọa độ điểm $C(x;y;z)$. Tính $P = x^3+y^3+z^3$.

Question 224. Cho hình hộp chữ nhật $ABCD.A'B'C'D'$ có $AB = 2; AD = 3; AA' = 4$. Chọn hệ trục tọa độ Oxyz có gốc O trùng với A, các điểm B; D; A' lần lượt thuộc Ox; Oy; Oz. Tìm tọa độ của $C'(x;3;z)$. Tính $P=x-z$.

Question 225. Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng 3, $SA =4$ và $SA \perp (ABCD)$. Chọn hệ trục Oxyz có gốc toạ độ tại A; các điểm B, D, S lần lượt trên các tia Ox, Oy, Oz. Gọi M là trung điểm SC. Tìm tọa độ điểm $M(x;y;z)$. Tính $T=x+y-\dfrac{3}{2}z$.

Question 226. Cho hình hộp $ABCD.A'B'C'D'$. Tính $|\vec{AC'}+\vec{CA'}+2\vec{CC'}|$.

Question 227. Cho hình hộp chữ nhật $ABCD.A'B'C'D'$ có $AB=8; AD=6; AA'=4$. Chọn hệ trục tọa độ Oxyz có gốc O trùng với A, các điểm B; D; A' lần lượt thuộc Ox; Oy; Oz. Tọa độ điểm $C'(x;y;z)$. Tính $P=x-2y+z$.

Question 228. Trong không gian Oxyz, cho hai vectơ $\vec{u} = (-1;5;0)$ và $\vec{v}=(1;-5;-3)$, tọa độ của vecto $\vec{u} + \vec{v}$ là