🧮 LỚP TOÁN THẦY BÌNH

Câu 1. Giá trị lớn nhất của hàm số $y = x(1 - x^2)$ trên khoảng $(0;1)$ là:

Câu 2. Cho hình hộp ABCD.A'B'C'D' . Phát biểu nào sau đây là đúng?

Câu 3. Trong không gian với hệ tọa độ $Oxyz$, cho tam giác $ABC$ biết $A(5; -2; 0), B(-2; 3; 0), C(0; 2; 3)$. Tìm toạ độ trọng tâm $G$ của tam giác $ABC$.

Câu 4. Trong không gian với hệ tọa độ Oxyz cho hai điểm $A(4;2;1), B(-2;-1;4)$. Tìm tọa độ điểm M thỏa mãn đẳng thức $\vec{AM}=2\vec{MB}$.

Câu 5. Tiệm cận ngang của đồ thị hàm số $y=\dfrac{x-2}{x+1}$ là

Câu 6. Cho hình lập phương ABCD.A'B'C'D' cạnh a. Khi đó $|\vec{AA'} + \vec{AD}|$ bằng

Câu 7. Trong không gian với hệ trục tọa độ Oxyz cho $M(4;5;6)$. Hình chiếu của M xuống mặt phẳng (Oxy) là $M'$. Xác định tọa độ $M'$.

Câu 8. Cho đồ thị hàm số $y=\dfrac{2x^2+x-5}{x+3}$ có đường tiệm cận xiên là đường thẳng $\Delta: y=ax+b$ với $a,b \in \mathbb{R}, a \ne 0$. Giá trị của tổng $a+b$ bằng

Câu 9. Giá trị của tiểu của hàm số $y = -x^4+2x^2+2$ bằng

Câu 10. Giá trị nhỏ nhất của hàm số $f(x)=-x^3-x+2$ trên đoạn $[-2;0]$ bằng?

Câu 11. Cho hàm số $y = \frac{2x^2-x+7}{x-1}$ có đồ thị (C). Biết rằng (C) có hai điểm cực trị, tính khoảng cách từ điểm $O$ đến đường thẳng đi qua hai điểm cực trị đó.

Câu 12. Trong không gian với hệ trục tọa độ $Oxyz$, cho $\vec{a} = (2;-3;3)$, $\vec{b} = (0;2;-1)$, $\vec{c} = (3;-1;5)$. Tọa độ của véctơ $\vec{u} = 2\vec{a} + 3\vec{b} - 2\vec{c}$ là:

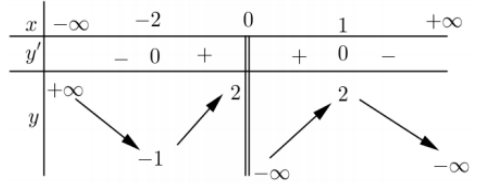
Câu 13. Cho hàm số $y=f(x)$ có bảng biến thiên như hình vẽ bên. Xét tính đúng, sai của các khẳng định sau:

Câu 14. Trong không gian Oxyz, cho $\vec{a} = (2;-1;3), \vec{b} = (-1;5;2)$

Câu 15. Trong không gian Oxyz, cho hình hộp $ABCD.A'B'C'D'$. Biết A(2;4;0), B(4;0;0) C(-1;4;-7) và D'(6;8;10).

Câu 16. Quan sát quá trình sinh trưởng và phát triển của một giống cà chua mới trong 18 tuần kể từ khi trồng, các kĩ sư thuộc một trung tâm giống cây trồng nhận thấy: chiều cao thân cây sau t tuần kể từ khi trồng được tính xấp xỉ bởi hàm số $h(t)=40\log_3(2t+1)+12$ (đơn vị: centimet, $0 \le t \le 18$). Sau 9 tuần kể từ khi trồng, hoa bắt đầu kết trái. Kể từ đó, đường kính trái cà chua ở tuần thứ $t$ xấp xỉ bởi hàm số $d(t)=3^{\frac{2t-17}{t-8}}-3$ (đơn vị: centimet, $9 \le t \le 18$).

Câu 17. Một nhà máy sản xuất x sản phẩm trong mỗi tháng. Chi phí sản xuất x sản phẩm được cho bởi hàm chi phí $C(x)=16000+500x-1,6x^2+0,004x^3$ (nghìn đồng). Biết giá bán của mỗi sản phẩm là một hàm số phụ thuộc vào số lượng sản phẩm x và được cho bởi công thức $p(x)=1700-7x$ (nghìn đồng). Hỏi mỗi tháng nhà máy nên sản xuất bao nhiêu sản phẩm để lợi nhuận thu được là lớn nhất? Biết rằng kết quả khảo sát thị trường cho thấy sản phẩm sản xuất ra sẽ tiêu thụ hết.

Câu 18. Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng 5, $SA = 2$ và $SA \perp (ABCD)$. Chọn hệ trục Oxyz có gốc toạ độ tại A; các điểm B, D, S lần lượt trên các tia Ox, Oy, Oz. Tọa độ điểm $C(x;y;z)$. Tính $P = x^3+y^3+z^3$.

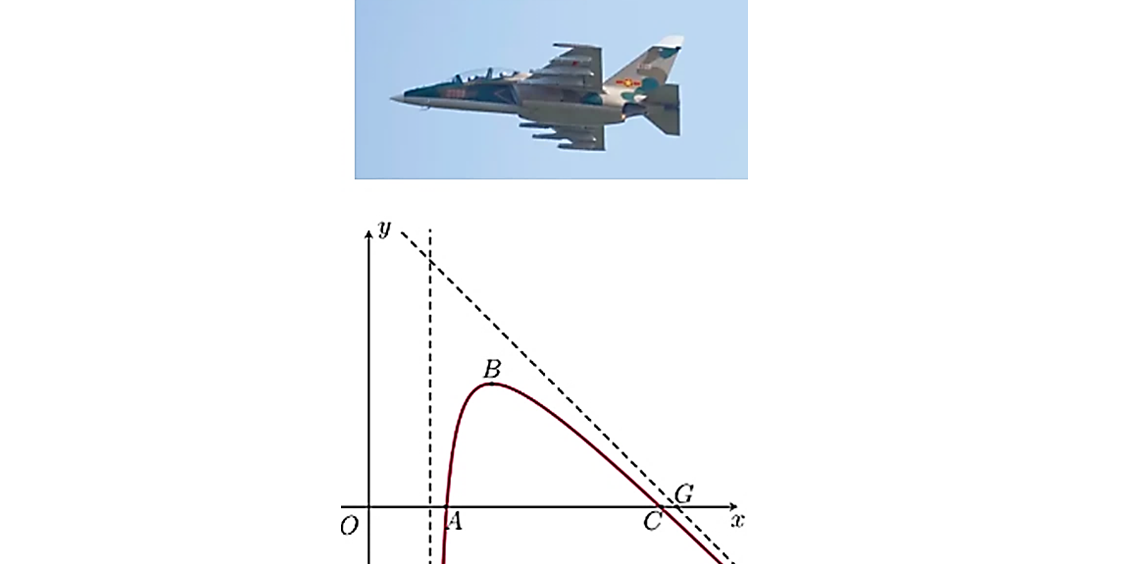
Câu 19. Một máy bay trình diễn có đường bay gắn với hệ trục $Oxy$ được mô phỏng như hình vẽ, trục $Ox$ gắn với mặt đất.
Đường bay có dạng là một phần của đồ thị hàm phân thức bậc hai trên bậc nhất $y=f(x)$ có đường tiệm cận đứng là $x=2$. Điểm $G$ là giao điểm của đường tiệm cận xiên của đồ thị hàm số $y=f(x)$ và trục $Ox$ được gọi là điểm giới hạn. Biết máy bay bay từ vị trí $A$ cách tọa tọa độ $O$ một khoảng 2,5 đơn vị và máy bay khi ở vị trí cao nhất cũng là điểm cực đại của hàm số cách điểm xuất phát 1,5 đơn vị theo phương song song với trục $Ox$ và cách mặt đất 4,5 đơn vị. Vị trí máy bay tiếp đất cách điểm giới hạn một khoảng bằng bao nhiêu?

Câu 20. Nhà máy A chuyên sản xuất một loại sản phẩm cho nhà máy B. Hai nhà máy thỏa thuận, mỗi tháng A cung cấp cho B tối đa 45 tấn sản phẩm và nếu số lượng đặt hàng là x tấn sản phẩm thì giá bán cho mỗi tấn sản phẩm là $P(x)=60-0,01x^2$ (triệu đồng). Chi phí để nhà máy A sản xuất x tấn sản phẩm trong một tháng là $C(x)=150+33x$ (triệu đồng) (gồm 150 triệu đồng chi phí cố định và 33 triệu đồng cho mỗi tấn sản phẩm). Để mỗi tháng thu được lợi nhuận lớn nhất thì A cần bán cho B bao nhiêu tấn sản phẩm?

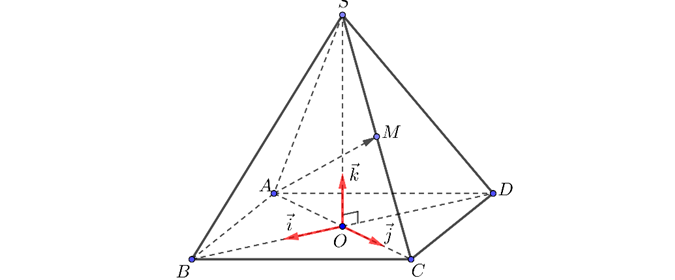
Câu 21. Trong không gian Oxyz, cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh bằng 5, giao điểm hai đường chéo AC và BD trùng với gốc O. Các vectơ $\vec{OB}, \vec{OC}, \vec{OS}$ lần lượt cùng hướng với $\vec{i}, \vec{j}, \vec{k}$ và $OA = OS=4$ như hình bên dưới. Toạ độ vectơ $\vec{AM} = (a;b;c)$ với M là trung điểm của cạnh SC, khi đó $a+b+c$ bằng bao nhiêu?

Câu 22. Một chiếc ô tô được đặt trên mặt đáy dưới của một khung sắt có dạng hình hộp chữ nhật với đáy trên là hình chữ nhật $ABCD$, mặt phẳng $(ABCD)$ song song với mặt phẳng nằm ngang. Khung sắt đó được buộc vào móc $E$ của chiếc cần cẩu sao cho các đoạn dây cáp $EA, EB, EC, ED$ có độ dài bằng nhau và cùng tạo với mặt phẳng $(ABCD)$ một góc bằng 60° (hình vẽ). Chiếc cần cẩu kéo khung sắt lên theo phương thẳng đứng. Trọng lượng của chiếc xe ô tô bằng bao nhiêu Niutơn? (làm tròn đến hàng đơn vị), biết rằng các lực căng $\vec{F_1}, \vec{F_2}, \vec{F_3}, \vec{F_4}$ đều có cường độ là 3500N và trọng lượng của khung sắt là 2500N.