CHUYÊN ĐỀ: ỨNG DỤNG ĐẠO HÀM
Môn Toán - Lớp 12
TÓM TẮT KIẾN THỨC
I. Tính đồng biến, nghịch biến của hàm số
Định Nghĩa
Kí hiệu \(K\) là khoảng, đoạn, hoặc nửa khoảng. Giả sử hàm số \(y = f(x)\) xác định trên \(K\). Ta nói hàm số \(y = f(x)\):- Được gọi là đồng biến trên \(K\) nếu \(\forall x_1, x_2 \in K, x_1 < x_2 \Rightarrow f(x_1) < f(x_2)\).
- Được gọi là nghịch biến trên \(K\) nếu \(\forall x_1, x_2 \in K, x_1 < x_2 \Rightarrow f(x_1) > f(x_2)\).
- Hàm số \(y = f(x)\) đồng biến trên \(K\) thì đồ thị đi lên từ trái sang phải.
- Hàm số \(y = f(x)\) nghịch biến trên \(K\) thì đồ thị đi xuống từ trái sang phải.
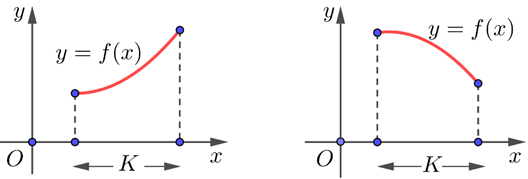
- Nếu \(f'(x)>0\) với mọi x thuộc \(K\) thì hàm số \(y = f(x)\) đồng biến trên \(K\).
- Nếu \(f'(x)<0\) với mọi x thuộc \(K\) thì hàm số \(y = f(x)\) nghịch biến trên \(K\).
- Định lí vẫn đúng trong trường hợp \(f'(x) = 0\) tại một số hữu hạn điểm trong \(K\).
- Nếu \(f'(x) = 0\) với mọi \(x \in K\) thì hàm số \(f(x)\) không đổi trên khoảng \(K\).
II. Cực trị của hàm số
Định Nghĩa
Cho hàm số \(y = f(x)\) xác định và liên tục trên khoảng \((a;b)\) (a có thể là \(-\infty\), b có thể là \(+\infty\)) và điểm \(x_0 \in (a;b)\).- Nếu tồn tại \(h > 0\) sao cho \(f(x) < f(x_0)\) với mọi \(x \in (x_0-h; x_0+h) \subset (a;b)\) và \(x \neq x_0\) thì ta nói hàm số \(f(x)\) đạt cực đại tại \(x_0\).
- Nếu tồn tại \(h > 0\) sao cho \(f(x) > f(x_0)\) với mọi \(x \in (x_0-h; x_0+h) \subset (a;b)\) và \(x \neq x_0\) thì ta nói hàm số \(f(x)\) đạt cực tiểu tại \(x_0\).
- Điểm cực đại/tiểu: \(x_0\).
- Giá trị cực đại/tiểu (cực trị): \(f(x_0)\), kí hiệu \(y_{CĐ}\) hoặc \(y_{CT}\).
- Điểm cực đại/tiểu của đồ thị: \(M_0(x_0; f(x_0))\).
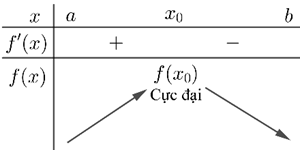
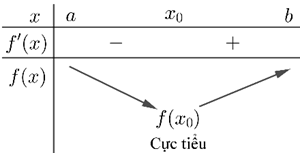
Giả sử hàm số \(y=f(x)\) liên tục trên khoảng \((a;b)\) chứa điểm \(x_0\) và có đạo hàm trên các khoảng \((a;x_0)\) và \((x_0;b)\). Khi đó:
- Nếu \(f'(x)\) đổi dấu từ âm sang dương khi \(x\) qua \(x_0\) thì \(x_0\) là một điểm cực tiểu.
- Nếu \(f'(x)\) đổi dấu từ dương sang âm khi \(x\) qua \(x_0\) thì \(x_0\) là một điểm cực đại.
Định lí trên được minh họa qua bảng biến thiên sau:
Ghi nhớ: Các bước tìm cực trị
- Tìm tập xác định của hàm số.
- Tính \(f'(x)\). Tìm các điểm mà tại đó \(f'(x)\) bằng 0 hoặc \(f'(x)\) không tồn tại.
- Lập bảng biến thiên và suy ra các điểm cực trị của hàm số.
Lưu ý:
Nếu \(f'(x_0)=0\) nhưng \(f'(x)\) không đổi dấu khi x qua \(x_0\) thì \(x_0\) không phải là điểm cực trị của hàm số.
CÁC DẠNG TOÁN VÀ PHƯƠNG PHÁP GIẢI
Dạng 1: Xét tính đơn điệu của hàm số cho bởi một công thức
Phương pháp giải:
- Tìm tập xác định \(D\) của hàm số.
- Tính đạo hàm \(f'(x)\). Tìm các điểm \(\{x_1; x_2; ...; x_n\} \in D\) mà tại đó đạo hàm \(f'(x)\) bằng 0 hoặc không tồn tại.
- Sắp xếp các điểm \(x_1, x_2, ..., x_n\) theo thứ tự tăng dần. Xét dấu \(f'(x)\) và lập bảng biến thiên.
- Nêu kết luận về các khoảng đồng biến, nghịch biến của hàm số.
VÍ DỤ MINH HỌA
Ví dụ 1: Xét tính đơn điệu (Hàm đa thức)
Dạng 1Xét tính đơn điệu của hàm số \(y = 4x^3 + 3x^2 - 36x + 6\).
Lời giải:
Tập xác định \(D=\mathbb{R}\).
Ta có: \(y' = 12x^2 + 6x - 36\). Cho \(y' = 0 \Leftrightarrow 12x^2 + 6x - 36 = 0 \Leftrightarrow \left[\begin{array}{l} x = -2 \\ x = \frac{3}{2} \end{array}\right.\)
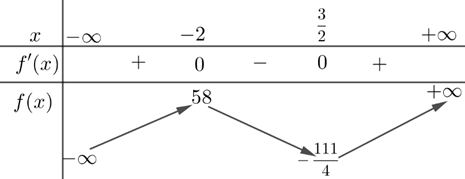
Kết luận: Hàm số đồng biến trên các khoảng \((-\infty; -2)\) và \((\frac{3}{2}; +\infty)\); nghịch biến trên khoảng \((-2; \frac{3}{2})\).
Ví dụ 2: Xét tính đơn điệu (Hàm phân thức)
Dạng 1Xét tính đơn điệu của hàm số \(f(x) = \frac{x-1}{x+1}\).
Lời giải:
Tập xác định \(D = \mathbb{R} \setminus \{-1\}\).
Ta có: \(f'(x) = \frac{1 \cdot (x+1) - 1 \cdot (x-1)}{(x+1)^2} = \frac{2}{(x+1)^2} > 0, \forall x \neq -1\).
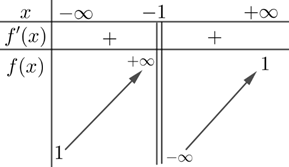
Kết luận: Hàm số đồng biến trên mỗi khoảng xác định là \((-\infty; -1)\) và \((-1; +\infty)\).
Ví dụ 3: Xét tính đơn điệu (Hàm chứa căn)
Dạng 1Xét tính đơn điệu của hàm số \(y = \sqrt{-x^2 + 4}\).
Lời giải:
Điều kiện: \(-x^2 + 4 \geq 0 \Leftrightarrow -2 \leq x \leq 2\). Tập xác định \(D = [-2; 2]\).
Ta có: \(y' = \frac{(-x^2+4)'}{2\sqrt{-x^2+4}} = \frac{-2x}{2\sqrt{-x^2+4}} = \frac{-x}{\sqrt{-x^2+4}}\). Cho \(y' = 0 \Rightarrow x=0\).
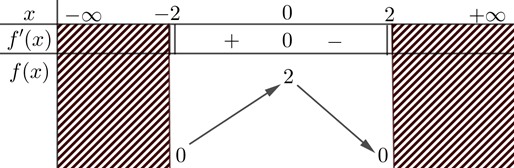
Kết luận: Hàm số đồng biến trên khoảng \((-2; 0)\) và nghịch biến trên khoảng \((0; 2)\).
Ví dụ 4: Xét tính đơn điệu (Hàm logarit)
Dạng 1Xét tính đơn điệu của hàm số \(y = \log_3(x^2 - 2x)\).
Lời giải:
Điều kiện: \(x^2 - 2x > 0 \Leftrightarrow x \in (-\infty; 0) \cup (2; +\infty)\).
Ta có: \(y' = \frac{(x^2-2x)'}{(x^2-2x)\ln 3} = \frac{2x-2}{(x^2-2x)\ln 3}\). Cho \(y' = 0 \Leftrightarrow 2x-2 = 0 \Leftrightarrow x=1\) (loại vì không thuộc tập xác định).

Kết luận: Hàm số nghịch biến trên khoảng \((-\infty; 0)\) và đồng biến trên khoảng \((2; +\infty)\).
Dạng 2: Xét tính đơn điệu của hàm số cho bởi đồ thị - bảng biến thiên
Phương pháp giải:
- Với đồ thị hàm số: Quan sát hướng lên – xuống của đường cong (theo chiều từ trái sang phải).
- Với bảng biến thiên: Quan sát hướng lên – xuống của mũi tên (theo chiều từ trái sang phải).
- Với bảng xét dấu: Quan sát dấu âm (-) hoặc dương (+) của \(f'(x)\).
VÍ DỤ MINH HỌA
Ví dụ 5: Đọc bảng biến thiên
Dạng 2Cho hàm số \(y=f(x)\) xác định trên \(\mathbb{R}\) và có bảng biến thiên như sau. Xét tính đơn điệu của hàm số.
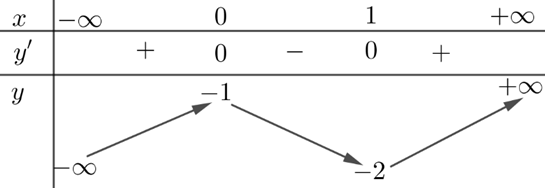
Lời giải:
Từ bảng biến thiên của hàm số, ta có:
- Trên khoảng \((-\infty;0)\) và \((1;+\infty)\), \(y'\) mang dấu "+", mũi tên đi lên.
- Trên khoảng \((0;1)\), \(y'\) mang dấu "-", mũi tên đi xuống.
Kết luận: Hàm số đồng biến trên các khoảng \((-\infty;0)\) và \((1;+\infty)\); nghịch biến trên khoảng \((0;1)\).
Ví dụ 6: Đọc đồ thị hàm số
Dạng 2Cho hàm số \(y = f(x)\) liên tục trên đoạn \([-3;3]\) và có đồ thị như hình bên. Xét tính đơn điệu của hàm số.
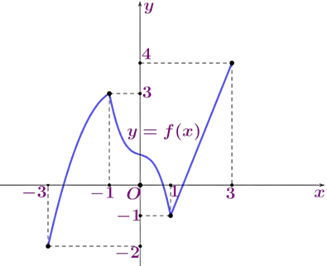
Lời giải:
Từ đồ thị của hàm số, ta quan sát chiều đi của đồ thị từ trái sang phải:
- Trên các khoảng \((-3;-1)\) và \((1;3)\), đồ thị có hướng "đi lên".
- Trên khoảng \((-1;1)\), đồ thị có hướng "đi xuống".
Kết luận: Hàm số đồng biến trên các khoảng \((-3;-1)\) và \((1;3)\); nghịch biến trên khoảng \((-1;1)\).
Dạng 3: Xác định cực trị của hàm số cho bởi công thức
Phương pháp giải:
- Tìm tập xác định \(D\) của hàm số.
- Tính đạo hàm \(f'(x)\). Tìm các điểm \(\{x_1; x_2; ...; x_n\} \in D\) mà tại đó \(f'(x)=0\) hoặc \(f'(x)\) không tồn tại.
- Lập bảng biến thiên dựa vào dấu của \(f'(x)\).
- Từ bảng biến thiên, kết luận về các điểm cực trị (nếu có).
Ví dụ 7: Tìm cực trị (Hàm đa thức bậc 3)
Dạng 3Tìm cực trị của hàm số \(y = 2x^3 - 3x^2 + 1\).
Lời giải:
Tập xác định: \(D=\mathbb{R}\).
Đạo hàm: \(y' = 6x^2 - 6x\). Cho \(y'=0 \Leftrightarrow 6x(x-1)=0 \Leftrightarrow \left[\begin{array}{l} x=0 \Rightarrow y=1 \\ x=1 \Rightarrow y=0 \end{array}\right.\)
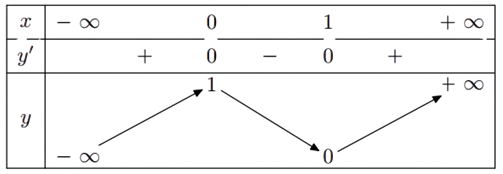
Kết luận: Hàm số đạt cực đại tại \(x=0\), \(y_{CĐ}=1\) và đạt cực tiểu tại \(x=1\), \(y_{CT}=0\).
Ví dụ 8: Tìm cực trị (Hàm đa thức bậc 4)
Dạng 3Tìm cực trị của hàm số \(y = -x^4 + 2x^3 - 2x - 1\).
Lời giải:
Tập xác định \(D = \mathbb{R}\).
Đạo hàm: \(y' = -4x^3 + 6x^2 - 2\). Cho \(y' = 0 \Leftrightarrow \left[\begin{array}{l} x = 1 \Rightarrow y = -2 \\ x = -\frac{1}{2} \Rightarrow y = -\frac{5}{16} \end{array}\right.\)

Kết luận: Hàm số đạt cực đại tại \(x = -\frac{1}{2}\), \(y_{CĐ} = -\frac{5}{16}\) và đạt cực tiểu tại \(x = 1\), \(y_{CT} = -2\).
Ví dụ 9: Tìm cực trị (Hàm phân thức bậc 1/bậc 1)
Dạng 3Tìm cực trị của hàm số \(y = \frac{x+2}{3x-1}\).
Lời giải:
Tập xác định: \(D = \mathbb{R} \setminus \{\frac{1}{3}\}\).
Đạo hàm: \(y' = \frac{1(3x-1) - 3(x+2)}{(3x-1)^2} = -\frac{7}{(3x-1)^2} < 0, \forall x \neq \frac{1}{3}\).
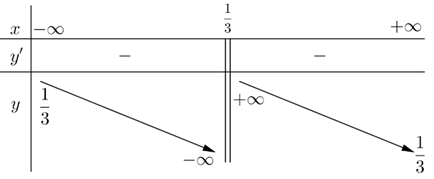
Kết luận: Vì \(y'\) không đổi dấu trên tập xác định nên hàm số không có cực trị.
Ví dụ 10: Tìm cực trị (Hàm phân thức bậc 2/bậc 1)
Dạng 3Tìm cực trị của hàm số \(y = \frac{x^2 - 4x + 4}{1-x}\).
Lời giải:
Tập xác định: \(D = \mathbb{R} \setminus \{1\}\).
Đạo hàm: \(y' = \frac{(2x-4)(1-x) - (-1)(x^2-4x+4)}{(1-x)^2} = \frac{-2x^2+6x-4+x^2-4x+4}{(1-x)^2} = \frac{-x^2+2x}{(1-x)^2}\).
Cho \(y' = 0 \Leftrightarrow -x^2+2x = 0 \Leftrightarrow \left[\begin{array}{l} x = 0 \Rightarrow y=4 \\ x = 2 \Rightarrow y=0 \end{array}\right.\)
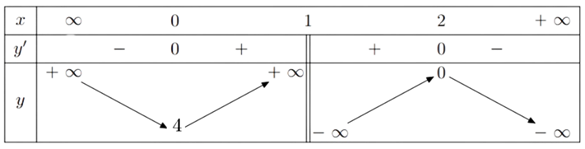
Kết luận: Hàm số đạt cực tiểu tại \(x=0\), \(y_{CT} = 4\) và đạt cực đại tại \(x=2\), \(y_{CĐ} = 0\).
Ví dụ 11: Tìm cực trị (Hàm mũ)
Dạng 3Tìm cực trị của hàm số \(f(x) = 2^{x^2-5x}\).
Lời giải:
Tập xác định: \(D = \mathbb{R}\).
Đạo hàm: \(f'(x) = (x^2-5x)' \cdot 2^{x^2-5x} \cdot \ln 2 = (2x-5) \cdot 2^{x^2-5x} \cdot \ln 2 \).
Cho \(f'(x)=0 \Leftrightarrow (2x-5) \cdot 2^{x^2-5x} \cdot \ln 2 = 0 \Leftrightarrow 2x-5=0 \Leftrightarrow x = \frac{5}{2}\).
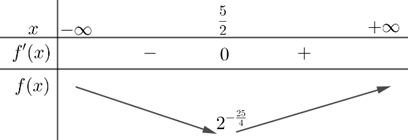
Kết luận: Hàm số đạt cực tiểu tại \(x = \frac{5}{2}\), \(y_{CT} = 2^{(\frac{5}{2})^2 - 5(\frac{5}{2})} = 2^{-\frac{25}{4}}\).
Dạng 4: Xác định cực trị của hàm số cho bởi bảng biến thiên - đồ thị
Phương pháp giải:
- Nhận xét: Hàm số \(f(x)\) có cực trị khi và chỉ khi đạo hàm \(y'\) đổi dấu khi đi qua điểm đó.
- Hàm số chỉ có thể đạt cực trị tại những điểm \(x_0\) mà tại đó đạo hàm triệt tiêu (\(f'(x_0)=0\)) hoặc đạo hàm không xác định.
VÍ DỤ MINH HỌA
Ví dụ 12: Tìm cực trị từ đồ thị f'(x)
Dạng 4Cho hàm số \(y=f(x)\) có đạo hàm trên \(\mathbb{R}\) và đồ thị hàm số \(y=f'(x)\) như hình bên. Đồ thị hàm số \(y=f(x)\) có bao nhiêu điểm cực tiểu và điểm cực đại?
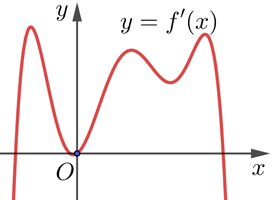
Lời giải:
Dựa vào đồ thị của \(y=f'(x)\), ta thấy \(f'(x)\) cắt trục hoành tại \(x=x_1, x=0, x=x_2\). Ta xét sự đổi dấu của \(f'(x)\) tại các điểm này:
- Khi \(x\) đi qua \(x_1\), đồ thị \(f'(x)\) đi từ dưới lên trên, tức là \(f'(x)\) đổi dấu từ âm sang dương. Do đó, hàm số \(f(x)\) đạt cực tiểu tại \(x=x_1\).
- Khi \(x\) đi qua \(0\), đồ thị \(f'(x)\) tiếp xúc với trục hoành và không đi qua, tức là \(f'(x)\) không đổi dấu. Do đó, hàm số \(f(x)\) không có cực trị tại \(x=0\).
- Khi \(x\) đi qua \(x_2\), đồ thị \(f'(x)\) đi từ trên xuống dưới, tức là \(f'(x)\) đổi dấu từ dương sang âm. Do đó, hàm số \(f(x)\) đạt cực đại tại \(x=x_2\).
Kết luận: Đồ thị hàm số \(y=f(x)\) có 1 điểm cực tiểu và 1 điểm cực đại.
Ví dụ 13: Tìm cực trị từ bảng biến thiên
Dạng 4Cho hàm số \(y = f(x)\) có bảng biến thiên như sau. Hàm số có bao nhiêu điểm cực tiểu và điểm cực đại?
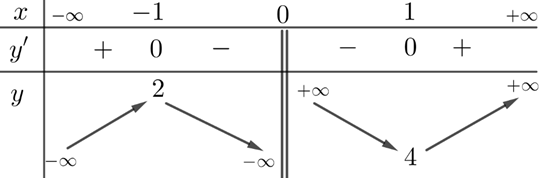
Lời giải:
Dựa vào bảng biến thiên, ta xét sự đổi dấu của \(y'\):
- Tại \(x=-1\), ta có \(y'=0\) và \(y'\) đổi dấu từ dương sang âm. Do đó, hàm số đạt cực đại tại \(x=-1\).
- Tại \(x=0\), cả \(y'\) và \(y\) đều không xác định nên đây không phải là điểm cực trị.
- Tại \(x=1\), ta có \(y'=0\) và \(y'\) đổi dấu từ âm sang dương. Do đó, hàm số đạt cực tiểu tại \(x=1\).
Kết luận: Đồ thị hàm số \(y = f(x)\) có 1 điểm cực đại và 1 điểm cực tiểu.
Ví dụ 14: Lập công thức hàm số từ BBT
Nâng caoCho hàm số \(y = f(x) = ax^3+bx^2+cx+d\) có bảng biến thiên như sau. Dựa vào bảng biến thiên, hãy thiết lập công thức hàm số \(y = f(x)\) đã cho.
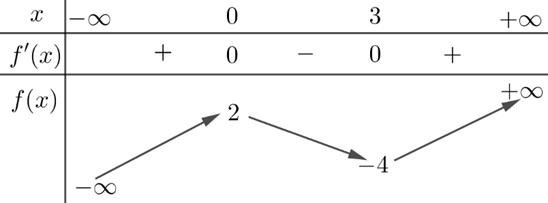
Lời giải:
Ta có đạo hàm: \(f'(x) = 3ax^2+2bx+c\).
Từ bảng biến thiên, ta thấy hàm số có hai điểm cực trị là \((0;2)\) (điểm cực đại) và \((3;-4)\) (điểm cực tiểu). Điều này có nghĩa là:
- Đồ thị đi qua điểm \((0;2)\) \(\Rightarrow f(0)=2\).
- Đạt cực trị tại \(x=0\) \(\Rightarrow f'(0)=0\).
- Đồ thị đi qua điểm \((3;-4)\) \(\Rightarrow f(3)=-4\).
- Đạt cực trị tại \(x=3\) \(\Rightarrow f'(3)=0\).
Ta có hệ phương trình:
Thay \(c=0, d=2\) vào hai phương trình cuối, ta được:
Kết luận: Vậy công thức của hàm số cần tìm là \(y = f(x) = \frac{4}{9}x^3-2x^2+2\).
Dạng 5: Toán thực tế áp dụng tính đơn điệu của hàm số
Bài toán chuyển động:
- Nếu hàm số \(s=f(t)\) biểu thị quãng đường di chuyển của vật theo thời gian \(t\), thì \(f'(t)\) là vận tốc tức thời của chuyển động tại thời điểm \(t\).
- Đạo hàm cấp hai \(f''(t)\) là gia tốc tức thời của chuyển động tại thời điểm \(t\).
VÍ DỤ MINH HỌA
Ví dụ 15: Chuyển động của khinh khí cầu
Toán thực tếTrong 8 phút đầu kể từ khi xuất phát, độ cao \(h\) (tính bằng mét) của khinh khí cầu vào thời điểm \(t\) phút được cho bởi \(h(t) = 6t^3 - 81t^2 + 324t\). Đồ thị của hàm số \(h(t)\) được biểu diễn như hình bên. Trong các khoảng thời gian nào khinh khí cầu tăng dần độ cao, giảm dần độ cao?
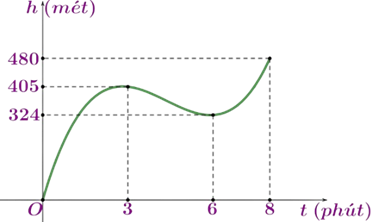
Lời giải:
Dựa vào đồ thị hàm số \(h(t)\), ta quan sát chiều đi lên/đi xuống của đồ thị:
- Đồ thị đi lên trên các khoảng \((0; 3)\) và \((6; 8)\). Điều này có nghĩa là độ cao của khinh khí cầu tăng dần.
- Đồ thị đi xuống trên khoảng \((3; 6)\). Điều này có nghĩa là độ cao của khinh khí cầu giảm dần.
Kết luận: Khinh khí cầu tăng dần độ cao trong 3 phút đầu tiên và trong khoảng thời gian từ phút thứ 6 đến phút thứ 8. Khinh khí cầu giảm dần độ cao trong khoảng thời gian từ phút thứ 3 đến phút thứ 6.
Ví dụ 16: Vận tốc của chất điểm
Toán thực tếXét một chất điểm chuyển động dọc theo trục Ox. Tọa độ của chất điểm tại thời điểm \(t\) (giây) được xác định bởi hàm số \(x(t) = t^3 - 6t^2 + 9t\) với \(t \ge 0\). Trong khoảng thời gian nào vận tốc của chất điểm tăng, trong khoảng thời gian nào vận tốc của chất điểm giảm?
Lời giải:
Vận tốc của chất điểm tại thời điểm \(t\) là \(v(t) = x'(t) = 3t^2 - 12t + 9\), với \(t \ge 0\).
Để xét tính đơn điệu của hàm vận tốc \(v(t)\), ta tính đạo hàm của nó:
\(v'(t) = (3t^2 - 12t + 9)' = 6t - 12\).
Cho \(v'(t)=0 \Rightarrow 6t - 12 = 0 \Rightarrow t=2\).
Lập bảng biến thiên cho hàm số \(v(t)\) trên \([0; +\infty)\):
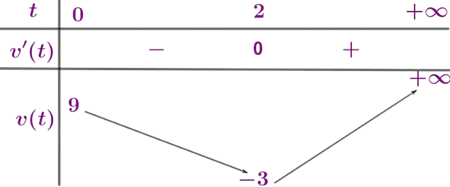
Kết luận: Dựa vào bảng biến thiên, vận tốc của chất điểm giảm trong khoảng \((0; 2)\) và tăng trong khoảng \((2; +\infty)\).
Ví dụ 17: Tìm hàm vận tốc từ đồ thị
Nâng caoMột vật chuyển động với vận tốc \(v(\text{km/h})\) phụ thuộc vào thời gian \(t(\text{h})\) có đồ thị dạng hàm bậc ba như hình bên. Biết tại \(t_1=1\)h vật có vận tốc \(v_1=4\)km/h và tại \(t_2=2\)h vật có vận tốc \(v_2=1\)km/h. Tính vận tốc của vật tại thời điểm \(t=3\)h.
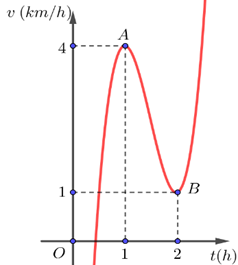
Lời giải:
Giả sử hàm số vận tốc có dạng: \(v(t) = at^3+bt^2+ct+d, t>0\).
Đạo hàm: \(v'(t) = 3at^2+2bt+c\).
Dựa vào đồ thị, hàm vận tốc đạt cực trị tại các điểm \(A(1;4)\) và \(B(2;1)\). Ta có hệ phương trình:
Vậy hàm vận tốc là: \(v(t) = 6t^3-27t^2+36t-11\) (km/h).
Vận tốc của vật tại thời điểm \(t=3\)h là:
Kết luận: Vận tốc của vật tại thời điểm \(t=3\)h là 16 km/h.
Dạng 6: Bài toán đơn điệu có chứa tham số
Phương pháp giải:
Hàm số bậc ba \(y=ax^3+bx^2+cx+d\)
- Để hàm số đồng biến trên \(\mathbb{R} \Leftrightarrow y' \ge 0, \forall x \in \mathbb{R} \Leftrightarrow \begin{cases} a>0 \\ \Delta_{y'} \le 0 \end{cases}\).
- Để hàm số nghịch biến trên \(\mathbb{R} \Leftrightarrow y' \le 0, \forall x \in \mathbb{R} \Leftrightarrow \begin{cases} a<0 \\ \Delta_{y'} \le 0 \end{cases}\).
Hàm số \(y=\frac{ax+b}{cx+d}\)
- Để hàm số đồng biến trên từng khoảng xác định \(\Leftrightarrow y' > 0 \Leftrightarrow ad-bc > 0\).
- Để hàm số nghịch biến trên từng khoảng xác định \(\Leftrightarrow y' < 0 \Leftrightarrow ad-bc < 0\).
VÍ DỤ MINH HỌA
Ví dụ 18: Tham số m với hàm bậc ba
Dạng 6Cho hàm số \(y = -\frac{1}{3}x^3 - mx^2 + (3m+2)x - 2\). Xác định \(m\) để hàm số nghịch biến trên \((-\infty; +\infty)\).
Lời giải:
Ta có \(y' = -x^2 - 2mx + 3m+2\).
Để hàm số nghịch biến trên \((-\infty; +\infty)\) thì \(y' \le 0, \forall x \in \mathbb{R}\).
Ta có: \(a = -1 < 0\) (luôn đúng).
Xét \(\Delta' = (-m)^2 - (-1)(3m+2) = m^2 + 3m + 2\).
Yêu cầu bài toán \(\Leftrightarrow \Delta' \le 0 \Leftrightarrow m^2+3m+2 \le 0 \Leftrightarrow -2 \le m \le -1\).
Kết luận: Giá trị \(m\) cần tìm là \(-2 \le m \le -1\).
Ví dụ 19: Tham số m với hàm phân thức
Dạng 6Cho hàm số \(y = \frac{2x-m}{x-1}\). Xác định \(m\) để hàm số đồng biến trên mỗi khoảng xác định của nó.
Lời giải:
Tập xác định: \(D = \mathbb{R} \setminus \{1\}\).
Ta có \(y' = \frac{2(-1) - (-m)(1)}{(x-1)^2} = \frac{m-2}{(x-1)^2}\).
Hàm số đồng biến trên mỗi khoảng xác định \(\Leftrightarrow y'>0, \forall x \in D\).
\(\Leftrightarrow m-2 > 0 \Leftrightarrow m > 2\).
Kết luận: Giá trị \(m\) cần tìm là \(m > 2\).
Dạng 7: Bài toán hàm hợp
Phương pháp giải (Xét tính đơn điệu của \(y=f(u(x))\)):
- Tính đạo hàm \(y'=u'(x) \cdot f'(u(x))\).
- Giải phương trình \(y'=0 \Leftrightarrow \left[ \begin{array}{l} u'(x)=0 \\ f'(u(x))=0 \end{array} \right.\).
- Dựa vào đồ thị/bảng biến thiên của \(f'(x)\) để giải phương trình \(f'(u(x))=0\).
- Lập bảng xét dấu cho \(y'\) và đưa ra kết luận.
VÍ DỤ MINH HỌA
Ví dụ 20: Đơn điệu hàm hợp từ BXD
Dạng 7Cho hàm số \(f(x)\) có bảng xét dấu đạo hàm như hình. Xác định các khoảng đồng biến của hàm số \(y = f(1-2x)\).

Lời giải:
Ta có, \(y' = (1-2x)' \cdot f'(1-2x) = -2f'(1-2x)\).
Hàm số đồng biến \(\Leftrightarrow y' \ge 0 \Leftrightarrow -2f'(1-2x) \ge 0 \Leftrightarrow f'(1-2x) \le 0\).
Dựa vào bảng xét dấu, \(f'(t) \le 0 \Leftrightarrow \left[ \begin{array}{l} t \le -3 \\ -2 \le t \le 1 \\ t \ge 3 \end{array} \right.\).
Áp dụng với \(t = 1-2x\), ta có:
Kết luận: Hàm số \(y=f(1-2x)\) đồng biến trên các khoảng \((-\infty;-1]\); \([0;\frac{3}{2}]\); \([2;+\infty)\).
Ví dụ 21: Đơn điệu hàm hợp từ đồ thị f'(x)
Dạng 7Cho hàm số \(y=f(x)\) có đồ thị đạo hàm \(y=f'(x)\) như hình vẽ. Xác định các khoảng nghịch biến của hàm số \(g(x)=f(x^2-2)\).
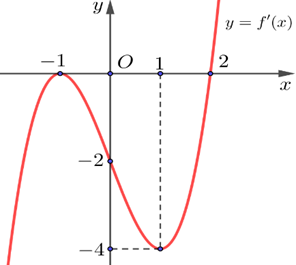
Lời giải:
Ta có \(g'(x)=(x^2-2)' \cdot f'(x^2-2) = 2x \cdot f'(x^2-2)\).
Giải \(g'(x)=0 \Leftrightarrow \left[ \begin{array}{l} 2x=0 \\ f'(x^2-2)=0 \end{array} \right.\). Từ đồ thị, \(f'(t)=0 \Leftrightarrow \left[ \begin{array}{l} t=-1 \\ t=2 \end{array} \right.\).
Lập bảng xét dấu cho \(g'(x)\):
Kết luận: Hàm số \(g(x)\) nghịch biến trên các khoảng \((-\infty;-2)\), \((0;1)\) và \((1;2)\).
Ví dụ 22: Cực trị hàm hợp
Dạng 7Cho hàm số \(y=f(x)\) có đạo hàm \(f'(x)=(x^2-1)(x-4)\) với mọi \(x \in \mathbb{R}\). Hàm số \(g(x)=f(3-x)\) có bao nhiêu điểm cực trị?
Lời giải:
Các nghiệm của \(f'(x)=0\) là \(x=1, x=-1, x=4\). Đây đều là các nghiệm đơn (bội lẻ).
Ta có: \(g'(x) = (3-x)' \cdot f'(3-x) = -f'(3-x)\).
Giải phương trình \(g'(x)=0 \Leftrightarrow f'(3-x)=0\).
Vì \(x=1, -1, 4\) là các nghiệm bội lẻ của \(f'(x)=0\), nên \(x=2, 4, -1\) cũng là các nghiệm bội lẻ của \(g'(x)=0\). Do đó, \(g'(x)\) đổi dấu qua 3 nghiệm này.
Kết luận: Hàm số \(g(x)=f(3-x)\) có 3 điểm cực trị.
Ví dụ 23: Cực tiểu hàm hợp từ BXD
Nâng caoCho hàm số \(y=f(x)\) có đạo hàm trên \(\mathbb{R}\) và có bảng xét dấu \(f'(x)\) như sau. Hỏi hàm số \(y=f(x^2-2x)\) có bao nhiêu điểm cực tiểu?
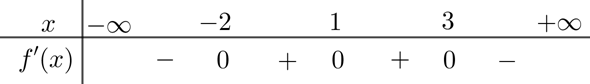
Lời giải:
Đặt \(g(x)=f(x^2-2x)\). Ta có \(g'(x)=(2x-2)f'(x^2-2x)\).
Giải \(g'(x)=0 \Leftrightarrow \left[ \begin{array}{l} 2x-2=0 \\ f'(x^2-2x)=0 \end{array} \right.\). Từ BXD, \(f'(t)=0 \Leftrightarrow t \in \{-2, 1, 3\}\).
Lập bảng xét dấu cho \(g'(x)\) với các nghiệm \(x \in \{-1, 1, 1-\sqrt{2}, 1+\sqrt{2}, 3\}\). Lưu ý rằng \(x^2-2x=1\) là nghiệm bội chẵn của \(f'(x^2-2x)\) nên \(g'(x)\) sẽ không đổi dấu qua \(x=1\pm\sqrt{2}\).
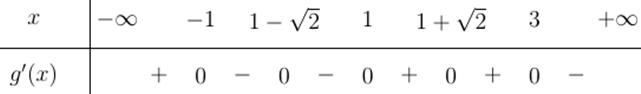
Từ bảng xét dấu, ta thấy \(g'(x)\) đổi dấu từ âm sang dương khi đi qua \(x=1\).
Kết luận: Hàm số \(y=f(x^2-2x)\) có đúng 1 điểm cực tiểu là \(x=1\).
